题目链接
题意:很长,读了很长时间才懂:
就是给一个物品评分,假设分数大于等于x,就将其判断为正数,否则判断为负数
这样判断肯定会出现一些误判,那么我们将判为负数的正数成为假正数(FN),将判为正数的负数成为假负数(FP)
其中判为正数的正数成为TP,判为负数的负数成为TN
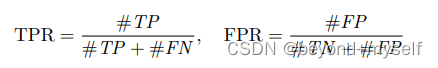
下面是要求的结果:

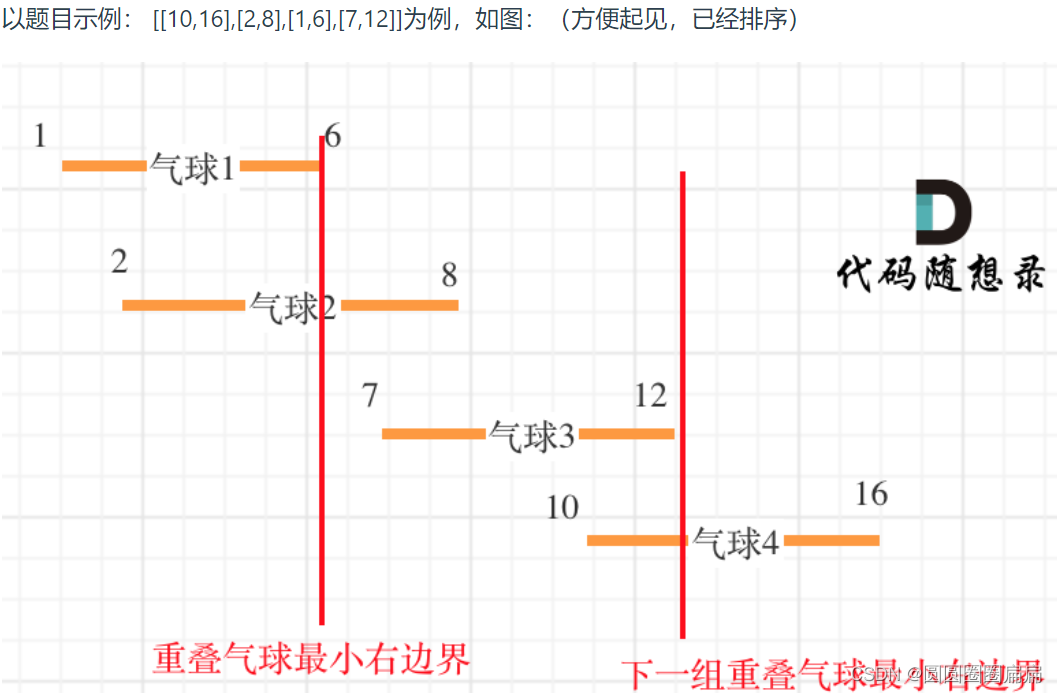
就是求出FPR<=r的最大值,然后求微分,其实也就是求下图中的面积:

做法:我们首先想到就是暴力,每次设置为输入的所有的值然后再一次循环找到每个值的情况(TP,TN,FP,FN),然后求出值。但是1e6太大,超时;所以我们想到去排序去解决问题
我们可以将初始值设置到无限大,这样先求出初始的状况,然后一步一步的往前递推即可(至于为什么开始的时候设置为最大而不是最小,下面会有解释)
具体的问题在代码中分析
下面是AC代码:
#include<iostream>
#include<cstring>
#include<algorithm>
#include<cstdio>
#include<bits/stdc++.h>
using namespace std;
const int N=1e6+10;
struct node
{
char op;
int v;
bool operator < (node &w)
{
if(v!=w.v) return v<w.v;
return op<w.op;
}
}a[N];
int main()
{
//如果是相同的直接
int tp=0,fp=0,tn=0,fn=0;
int n;
cin>>n;
//假设初始值为0
for(int i=1;i<=n;i++)
{
cin>>a[i].op>>a[i].v;
if(a[i].op=='+') fn++;
if(a[i].op=='-') tn++;
}
sort(a+1,a+1+n);
double ans=0;
double prefix=0;
for(int i=n;i>=1;i--)//这里应该从后往前遍历,因为从前往后没有一个从上一个状态到下一个状态的转换过程:假设我们将初始的设置为最小值,那么当前的正数在上一次设置为真正数,这次仍然为真正数;当前的负数上一次被设置为假正数,这次仍然为假正数,所以没有一个变化的过程,究其根本,就是题中的关系是一个>=的关系,即>=的本数的被设置为正数;所以从>到=是没有变化的,而如果本题改成了>关系,就可以从前往后,而不是从后往前了。
{
if(a[i].op=='-')//假设这次为负数,上次被设置为了真负数,这次被设置为了假正数
{
tn--;
fp++;
}
else//假设这次为正数,上次被设置为了假负数,这次被设置为了真正数
{
fn--;
tp++;
}
ans+=1.0*tp/(tp+fn)*(1.0*fp/(tn+fp)-prefix);//具体的可以看一下图,我们求面积一定要减去前面的一块
prefix=1.0*fp/(tn+fp);//更新前面横坐标值
}
printf("%.10lf",ans);
return 0;
}
这个题还有一个要注意的点是我们一定是当两个数相等的时候我们一定要将+放在前面,这样从后往前暴力的时候先便利的是‘-’,即先更新的是横坐标,这样可以保证得到的坐标都是非递减的,这样求得值才会是正确的(这是网上的大多数答案,我理解了很久,也不是很理解),我从数据方面理解了一下,我们看到下面的数据:(测试样例第三组)
我们分析一下第三组测试样例:
设判断值=34时:
TP=2,FP=2,TN=2,FN=2
此时TPR=0.5,FPR=0.5
设判断值=38时:
TP=1,FP=1,TN=3,FN=3
此时TPR=0.25,FPR=0.25
上面34和排完序与34相邻的数38的数据

这个是按照‘-‘排在前面的方法,我们看那个+34和-34的数据,发现纵坐标先改变,也就是当FPR=0.25的时候,TPR可以等于0.5这是错误的,因为这里是不会产生突变的。我们再看题目中给的图这也是错误的。
而下面是正确的数据:

我们发现,这个里面就是只有等于FPR=0.5的时候TPR=0.5,而那个0.25只是一个中间数据,作为一个转折点,因为他是一个突变,我们不能斜着画线,所以我们突变前的那个中间数据算。这个题第三组样例给的很好,应该是暗示往哪方面想。