前言

本文将基于UoA的课件介绍机器学习中的集成学习。

We will cover:
Averaging, Random Forests, AdaBoost, XGBoost

涉及的英语比较基础，所以为节省时间（不是full-time，还有其他三门课程，所以时间还是比较紧的），只在我以为需要解释的地方进行解释。

此文不用于任何商业用途，仅仅是个人学习过程笔记以及心得体会，侵必删。

Ensembles

集成学习是一种机器学习技术，通过将多个模型的预测结果进行整合，得到一个更准确、更稳定的预测结果。集成学习可以用于分类、回归、聚类等各种机器学习任务。

集成学习可以提高模型的稳定性和泛化能力，减少过拟合现象，使得模型对噪声数据更具有鲁棒性。

Averaging,

Averaging是一种集成学习方法，它是基于Bagging思想的一种简单的集成方法。它的基本思想是通过对多个基分类器的预测结果进行平均或加权平均来得到最终预测结果。

Averaging方法首先使用随机有放回抽样的方法，从原始数据集中生成多个子集，每个子集用于训练一个独立的基分类器。然后在测试时，每个基分类器对测试样本进行预测，最终的预测结果是所有基分类器的预测结果的平均值或加权平均值。

Averaging方法的优点是实现简单，易于并行化，可以有效地减少模型的方差，提高模型的稳定性和泛化能力。它适用于各种机器学习任务，特别是在训练数据量较少的情况下，Averaging方法可以通过生成多个子集来增加样本量，提高模型的性能。

Stacking

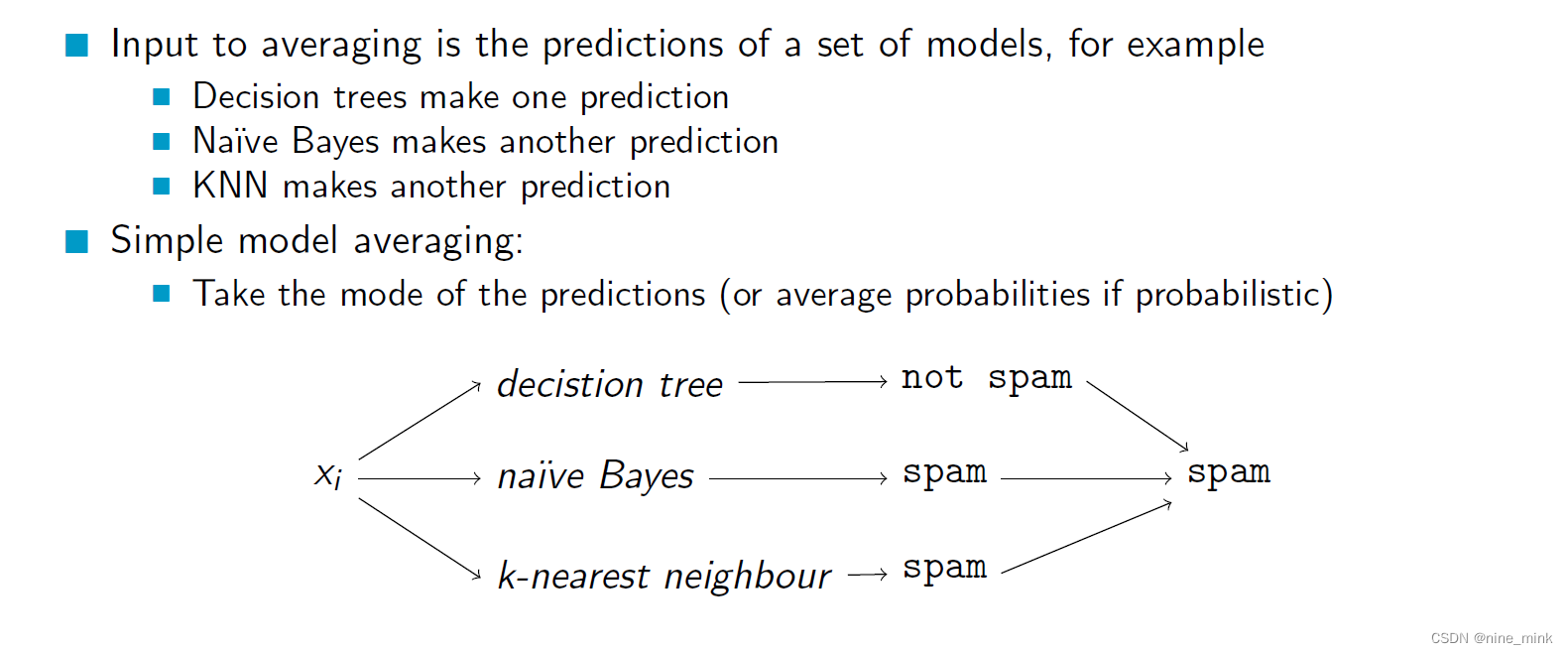
Stacking是一种集成学习方法，它可以将多个基分类器组合在一起，通过结合不同基分类器的优点，得到一个更准确的最终预测结果。Stacking方法的基本思想是通过将多个基分类器的预测结果作为新的特征输入到另一个分类器中进行训练。

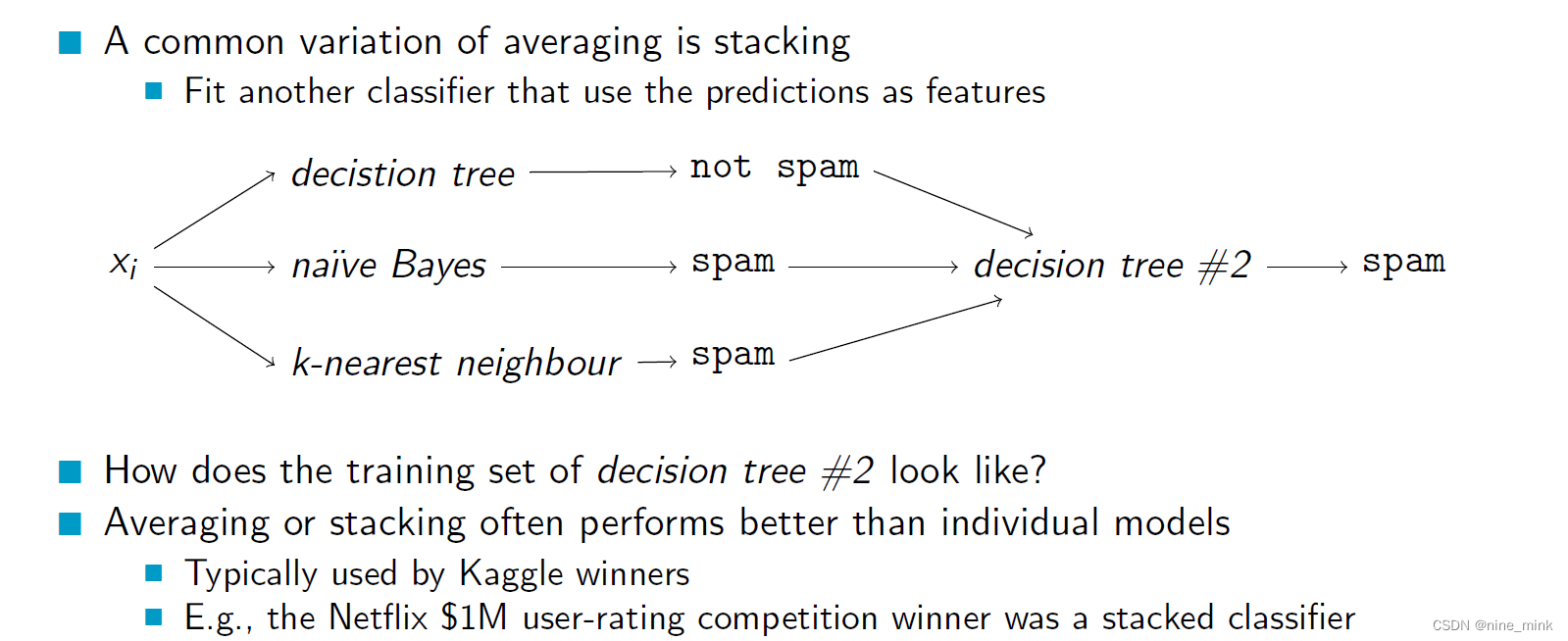
Stacking方法首先将原始数据集分为两部分：训练集和验证集。然后使用训练集对多个不同类型的基分类器进行训练。接着，对于每个基分类器，使用训练集对其进行预测，将预测结果作为新的特征，与原始数据集合并得到新的数据集。最后，使用新的数据集和验证集对另一个分类器（称为元分类器）进行训练，得到最终的预测结果。

Stacking方法的优点是可以利用多个基分类器的优势，提高模型的性能和稳定性，同时避免了单个分类器的缺点。但是，Stacking方法需要更多的计算资源和时间，因为需要训练多个基分类器和一个元分类器。此外，Stacking方法也更容易过拟合，需要谨慎地选择基分类器和元分类器。

Why does averaging work?

很简单，没啥可说的。

如何理解：In practice errors won’t be completely independent due to noise in the labels

在Averaging方法中，每个基分类器使用不同的随机子集训练，因此它们是相互独立的。然而，在实践中，由于数据集中可能存在噪声数据或标签错误，基分类器之间的误差可能不是完全独立的。

例如，如果数据集中存在标签错误，那么在随机有放回地抽样生成不同子集时，相同的错误数据可能会被包含在不同的子集中，从而使得多个基分类器之间出现一定的相关性。这种相关性可能导致基分类器的预测结果更加一致，从而使得集成模型的方差没有完全减少，无法达到预期的效果。

为了避免这种情况，可以使用一些技术来减少标签噪声或增加数据样本，例如数据清洗、数据增强等方法。此外，也可以考虑使用更复杂的集成方法，例如Bagging和Boosting等方法，这些方法可以通过改变基分类器之间的关系来减少误差的相关性，从而提高模型的性能。

Random Forests

随机森林是一种基于决策树的集成学习方法，它通过Bagging方法和随机特征选择的方式，构建多个决策树并将它们组合起来，得到一个更加准确的预测结果。

Does averaging work if you use trees with the same parameters?

Yes, averaging can work even if you use trees with the same parameters, but the performance improvement may not be as significant as when using trees with different parameters.

When trees have the same parameters and are trained on the same dataset, they are likely to have similar biases and errors, which can limit the diversity of the ensemble. As a result, averaging the predictions of these trees may not lead to significant improvements in accuracy compared to a single decision tree.

However, averaging can still be beneficial in some cases. For example, if the dataset is noisy, averaging can help to reduce the effect of random errors in individual trees and improve the overall performance of the ensemble. In addition, if the dataset is small, averaging can help to stabilize the predictions and reduce the variance of the model.

In practice, it is often beneficial to use trees with different parameters and/or different subsets of features when constructing a decision tree ensemble. This can increase the diversity of the ensemble and lead to better performance.

Bootstrap Sampling

Bootstrapping: Bootstrapping is a statistical technique that involves sampling with replacement from the original dataset to create multiple new datasets. In the context of Random Forests, bootstrapping is used to generate multiple subsets of the original dataset, each of which is used to train a decision tree. This process is called Bagging (Bootstrap Aggregating).
The bootstrapping process introduces randomness into the dataset, which helps to reduce the correlation between the decision trees and improve the accuracy of the ensemble. By generating multiple subsets of the data, the algorithm can capture different aspects of the data and reduce the risk of overfitting.

Bagging and Random Forests are both ensemble learning techniques that use multiple models to improve the accuracy and robustness of predictions. The main difference between the two lies in the way the individual models are trained and combined.

Bagging is a technique that involves randomly sampling subsets of the original dataset with replacement, and training a separate model on each subset. Each model is trained independently of the others, and the final prediction is made by averaging the predictions of all the models.

Random Forests, on the other hand, use a modified form of decision trees known as “randomized decision trees”, which introduce additional randomness into the modeling process. In addition to randomly sampling subsets of the data, Random Forests also randomly select a subset of features at each split in the decision tree. By introducing this additional level of randomness, Random Forests are able to produce more diverse models, which can lead to improved accuracy and robustness.

So, while Bagging is primarily a data sampling technique, Random Forests incorporate both data sampling and feature selection techniques to improve model performance.
这个百分比是通过统计学中的中心极限定理得出来的。中心极限定理指出，对于一个具有有限方差的随机变量，在随机抽样下，其样本平均值的分布会趋近于正态分布，且随着样本数量的增加，逼近程度越来越高。具体而言，在二项分布中，当样本容量足够大时，每个数据子集的样本数量大约为原始数据集样本数量的63.2%左右。这个数值被称为"一倍标准差"，可以通过计算标准差来推算。

Random Trees

Random trees: In addition to bootstrapping, Random Forests also uses randomization in the construction of individual decision trees. Specifically, at each node of the decision tree, a random subset of the available features is selected to determine the best split. This ensures that each tree is constructed using a different set of features, which further increases the diversity of the ensemble.

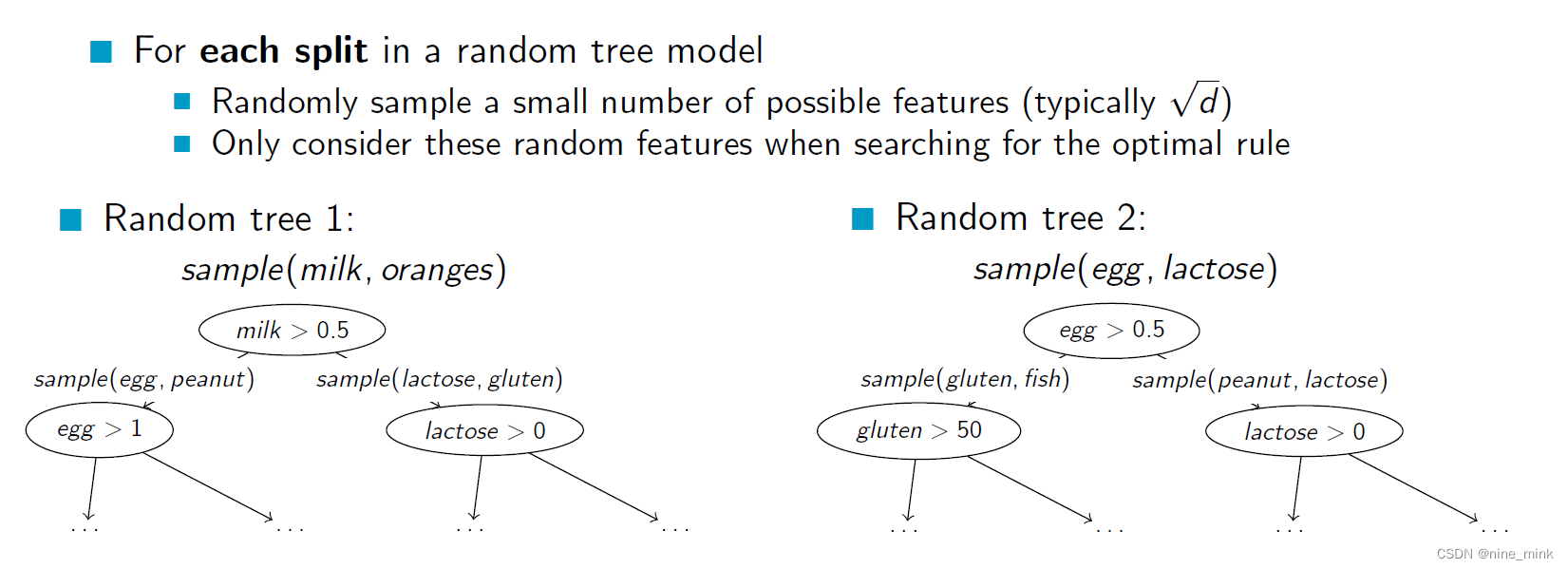
The combination of bootstrapping and random trees results in a powerful algorithm that is robust to overfitting and can handle high-dimensional datasets with complex relationships between the features and the target variable. Random Forests have been widely used in many applications, such as classification, regression, and feature selection.

AdaBoost

AdaBoost (Adaptive Boosting) is a machine learning algorithm that is used for classification and regression problems. It works by combining multiple “weak” models into a “strong” model. In AdaBoost, each weak model is trained on a weighted version of the training data, where the weights are adjusted based on the performance of the previous weak models. The final prediction is made by combining the predictions of all the weak models.

The key idea behind AdaBoost is to iteratively improve the performance of the weak models by focusing on the examples that are misclassified by the previous models. In each iteration, the weights of the training examples are adjusted so that the misclassified examples are given a higher weight. This means that the next weak model will focus more on these examples, and hopefully be able to classify them correctly.
In AdaBoost, the final prediction is made by taking a weighted vote of the predictions of the individual base classifiers. The weights assigned to each base classifier are based on their accuracy on the training data.

Specifically, after each round of boosting, the weights of the training examples are adjusted such that the examples that were misclassified by the previous round of classifiers are given higher weights. The base classifiers are then retrained on the updated weights.

After all of the base classifiers have been trained, the final prediction is made by taking a weighted vote of their predictions, with the weights of each classifier being proportional to its accuracy on the training data. This means that the more accurate classifiers are given higher weights in the final prediction.

By combining the predictions of multiple base classifiers, AdaBoost is able to create a stronger classifier that is less likely to overfit to the training data.The AdaBoost algorithm is designed to work with “weak” base classifiers, which are classifiers that have a classification accuracy that is only slightly better than random guessing. The reason for using weak classifiers is that AdaBoost can then combine them to create a strong classifier that has a high classification accuracy.

However, there are some types of base classifiers that are not suitable for use with AdaBoost. These include:

1. Deep decision trees: Deep decision trees are not suitable for use as base classifiers in AdaBoost because they typically have a very low training error rate, which means that there is little room for improvement. Since AdaBoost relies on the base classifiers being slightly better than random guessing, using deep decision trees can actually decrease the performance of the algorithm.

2. Decision stumps with infogain: Decision stumps are shallow decision trees with only one split. While decision stumps can be used as base classifiers in AdaBoost, using the infogain criterion to choose the splitting variable does not guarantee that the resulting classifier will have a classification accuracy that is greater than 50%. This is because the infogain criterion does not take into account the weights of the training examples.

3. Weighted logistic regression: Logistic regression is a popular algorithm for binary classification problems. However, using weighted logistic regression as a base classifier in AdaBoost does not guarantee that the resulting classifier will have a classification accuracy that is greater than 50%. This is because the logistic regression model is not guaranteed to have a decision boundary that can separate the two classes with a high accuracy.

In general, suitable base classifiers for AdaBoost include simple decision trees or decision stumps with other splitting criteria (such as Gini index or misclassification rate), linear classifiers (such as linear SVM or perceptron), and neural networks with a small number of hidden units.

AdaBoost不仅给数据加权还给分类器加权

在AdaBoost算法中，不仅给训练数据集中的每个样本赋予权重，还给每个弱分类器（Weak Classifier）赋予权重。这个权重是基于分类器的性能来计算的。在每一轮迭代中，AdaBoost会根据上一轮分类器的表现来调整样本和分类器的权重，以提高分类的准确性。这样，AdaBoost会逐步地构建出一个较强的分类器。因此，AdaBoost算法既利用了加权样本来训练分类器，又利用了加权分类器来提高分类效果。

这种训练模式使得最后一个分类器权重非常高？

AdaBoost算法的训练过程会不断增加那些被之前的分类器错分的样本的权重，这样最后一些分类器就会更关注那些难以分类的样本，从而提高整个模型的泛化能力。

另外，AdaBoost在每一轮迭代中都会为每个弱分类器分配一个权重，该权重是基于分类器的分类准确率计算的。那些准确率高的分类器会被赋予较高的权重，从而在模型最终预测时占据更重要的地位。因此，最后一个分类器通常会获得更高的权重，对整个模型的分类结果产生更大的影响。

训练新的分类器时，AdaBoost会利用之前的分类器集合和加权样本来构建一个损失函数（Loss Function），该损失函数的作用是最小化之前分类器集合和新分类器的分类误差。因此，新分类器的训练是在之前分类器集合的基础上进行的，而且它也会对之前的分类器集合进行操作，使得之前分类器集合的分类能力得到提升。

需要注意的是，AdaBoost算法中的弱分类器通常是决策树或者其他简单的分类器，这些分类器的训练通常是独立的。因此，在训练新的分类器时，不会对之前的分类器进行修改或者重训练，而是基于之前的分类器集合来构建新的分类器，从而逐步提高整个模型的分类能力。

AdaBoost is a powerful algorithm that can achieve high accuracy even with a relatively small number of weak models. It is often used in practice for tasks such as face detection, object recognition, and text classification. However, it can be sensitive to outliers and noisy data, and may not perform as well on datasets with a large number of features or classes.

XGBoost

XGBoost (eXtreme Gradient Boosting) is a popular machine learning algorithm that is based on the gradient boosting framework. Like other boosting algorithms, XGBoost works by combining the predictions of multiple “weak” models to create a strong model.

正则化回归树（Regularized Regression Trees）是一种结合了回归树和正则化方法的算法。它在回归树的基础上添加了L1正则化（Lasso）或L2正则化（Ridge）惩罚项，以避免模型出现过拟合问题。

回归树是一种基于树结构的回归模型，通过将输入空间划分为若干个子空间，并在每个子空间上拟合一个常量来构建模型。回归树能够自适应地选择划分变量和划分点，并且具有较好的解释性。但是，由于回归树容易出现过拟合问题，因此需要一些方法来控制模型的复杂度。

正则化回归树采用L1或L2正则化方法来控制模型的复杂度。L1正则化可以产生稀疏的系数，可以用于特征选择，而L2正则化可以平滑系数，避免系数过大。在正则化回归树中，对于每个叶子节点，引入L1或L2正则化惩罚项，将叶子节点的输出值作为常量，从而在保持树结构的情况下，控制模型的复杂度。

正则化回归树通常使用交叉验证来选择正则化参数，并且在使用正则化回归树进行预测时，需要使用与训练时相同的正则化参数

Regularization

Regularization is a technique used in machine learning to prevent overfitting, which is a common problem in complex models that can memorize the training data and fail to generalize to new, unseen data. Regularization introduces a penalty term to the loss function that encourages the model to learn simpler and more generalizable patterns, rather than memorizing noise or outliers in the training data.

There are several types of regularization techniques commonly used in machine learning:

1. L1 regularization (also known as Lasso regularization): Adds a penalty proportional to the absolute value of the model coefficients, which encourages sparsity and eliminates some features altogether.

2. L2 regularization (also known as Ridge regularization): Adds a penalty proportional to the square of the model coefficients, which encourages smaller and more spread-out coefficients.

3. Dropout regularization: Randomly drops out some of the nodes in the neural network during training, which forces the remaining nodes to learn more robust and independent representations.

4. Early stopping: Stops the training process before the model overfits the training data by monitoring the validation error and stopping when it starts to increase.

5. Data augmentation: Increases the size of the training set by adding new examples that are similar to the existing ones, which helps the model generalize better to new data.

By using regularization, machine learning models can achieve better performance on unseen data, reduce overfitting, and improve their ability to generalize to new situations.

Gradient Boosting

Gradient boosting is a popular machine learning technique that combines multiple weak learners (usually decision trees) to create a strong learner.

The basic idea behind gradient boosting is to iteratively add new models to the ensemble, each one attempting to correct the errors made by the previous models. Specifically, at each iteration, the algorithm trains a new model on the residuals (the differences between the predicted values and the actual values) of the previous model. The new model is then added to the ensemble, and the process is repeated until the desired level of performance is achieved.

Gradient boosting has several advantages over other ensemble methods. For one, it can handle a wide variety of data types and can be used for both regression and classification problems. Additionally, it is less prone to overfitting than other ensemble methods, as each new model in the ensemble is trained to correct the errors of the previous models.

One popular implementation of gradient boosting is XGBoost, which is known for its speed and scalability, as well as its ability to handle complex data types and customizable loss functions. Other popular implementations of gradient boosting include LightGBM and CatBoost.

对于AdaBoost来说，下一个分类器的训练基于上一个week module出错的样本并给出错样本加权，使下一个分类器更加关注更容易出错的样本，这种策略可不可以理解为梯度提升的策略

Yes, you can think of AdaBoost as a type of gradient boosting algorithm. Both AdaBoost and gradient boosting aim to improve the performance of a weak learner by iteratively adding new models to the ensemble that correct the errors made by the previous models.

In AdaBoost, the next classifier is trained on the misclassified samples of the previous classifier, and the misclassified samples are given higher weights to make the next classifier focus more on the difficult samples. This is similar to gradient boosting, where each new model is trained on the residuals (the differences between the predicted values and the actual values) of the previous model.

The key difference between AdaBoost and other gradient boosting algorithms, such as XGBoost, is the way in which the weights of the samples are updated. In AdaBoost, the weights are updated using an exponential loss function, while in other gradient boosting algorithms, the weights are typically updated using a differentiable loss function, such as the mean squared error or the cross-entropy loss. Additionally, AdaBoost uses decision stumps as weak learners, while other gradient boosting algorithms can use a wider range of weak learners, such as decision trees or linear models.

Regression Trees

XGBoost（eXtreme Gradient Boosting）是一种基于梯度提升决策树（Gradient Boosting Decision Trees，GBDT）的机器学习算法，它在GBDT的基础上添加了一些新的技术，如正则化、缺失值处理和分布式计算等，提高了模型的性能和稳定性。

在XGBoost中，回归树是作为弱学习器（Weak Learner）使用的。XGBoost使用一种特殊的回归树——CART回归树（Classification and Regression Tree），它可以用于二分类、多分类和回归任务。CART回归树通过递归地将输入空间划分为若干个子空间，并在每个子空间上拟合一个常量来构建模型。在XGBoost中，回归树通常是二叉树，每个非叶子节点对应一个划分特征和划分点，叶子节点对应一个输出值。

XGBoost采用梯度提升算法来训练回归树。在每轮迭代中，XGBoost会计算当前模型的梯度和Hessian矩阵，并使用梯度和Hessian矩阵来构建一棵新的回归树。为了防止过拟合，XGBoost采用了正则化技术，如L1正则化和L2正则化，以控制模型的复杂度。

XGBoost还采用了一些其他的技术来提高模型的性能和稳定性，如缺失值处理、直方图近似、分布式计算等。缺失值处理可以有效地处理缺失值，直方图近似可以加速计算过程，分布式计算可以处理大规模数据。

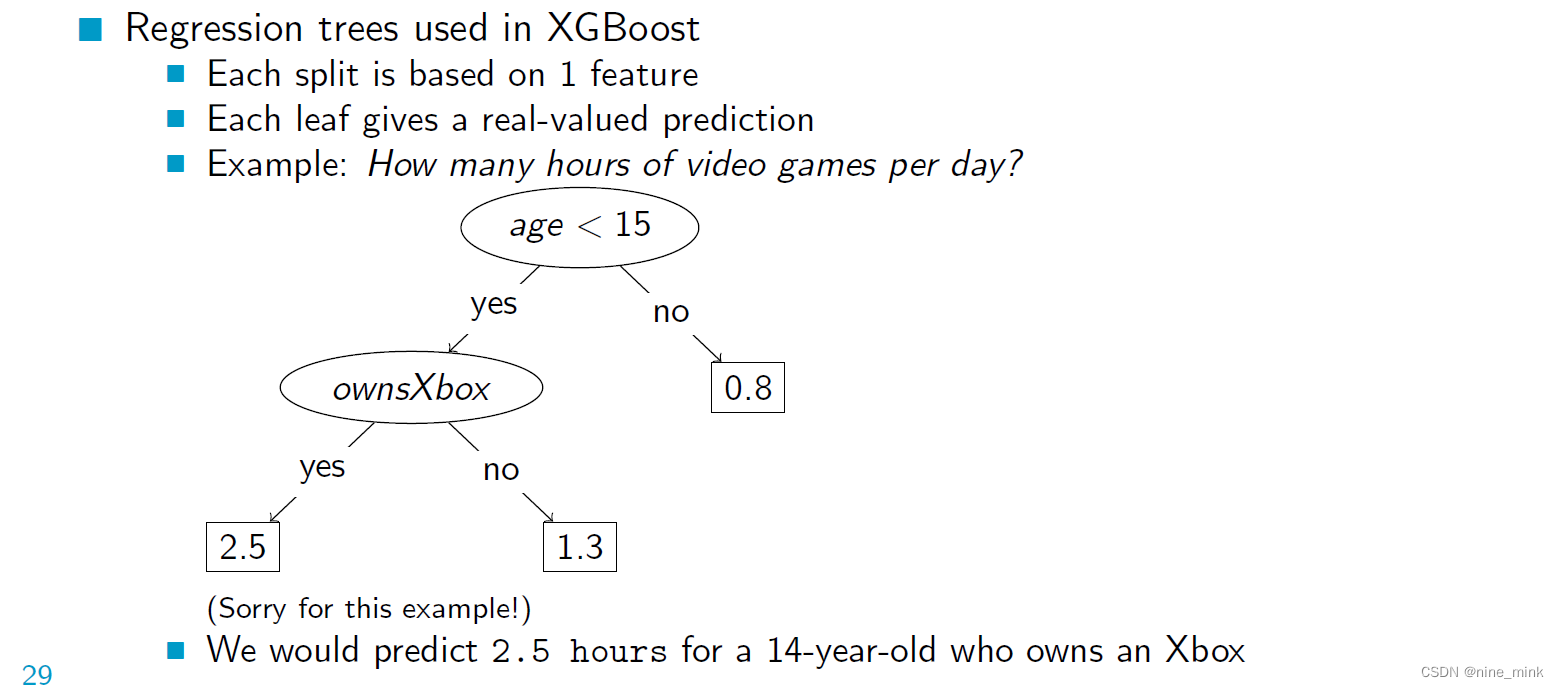
为了拟合回归树，我们可以使用一种简单的方法，我们预测分配给树的每个叶子的训练输出值(yi)的平均值。每个叶节点的权重(wL)设为该节点上yi的平均值。然后，我们通过设置wL值来训练模型，以最小化预测值与实际输出值的平方误差。

换句话说，我们通过基于输入特征的值递归地将数据分成更小的子集来构建决策树。在每一步中，我们选择使每个子集的预测输出值的平方误差最小的特征和分裂点。我们重复这个过程，直到我们达到一个停止标准，比如最大树深度或每片叶子的最小样本数。

这种方法的优点是它简单且易于解释，并且可以以与决策树相同的速度进行训练。但是，它使用均值而不是模式来预测输出值，并且使用平方误差而不是精度或信息再来衡量分割的质量。此外，它使用贪婪策略来生长树，这可能并不总是产生最优解。

想想决策树入门的那篇，这里的决策本质上其实是一样的

Boosted Regression Trees: Prediction

假设有许多回归树对某个数据点进行预测，对于某个数据点 i，每个回归树都会给出一个连续的预测值，如上面的例子所示。每个回归树的预测值可以看做是对真实值的一个偏差或误差，这个误差有可能是正的，也有可能是负的。在XGBoost中，这些回归树的预测值会被简单地相加，作为最终的预测结果，如上面的公式所示。这相当于将每个回归树的预测结果看做是对真实值的一个修正，最终将这些修正相加起来得到最终的预测结果。

在提升方法中，我们不像随机森林那样使用均值。相反，每棵树都不是单独地尝试预测真实的yi值（我们假设它们欠拟合）。而是，每棵新树都试图修正旧树所做的预测，使其总和为yi。因此，每个新树都是在上一个树的基础上构建，通过拟合残差来进一步提高模型的预测性能。最终的模型是所有树的加权和，其中权重由每棵树的训练误差决定。这种方法可以有效地降低偏差和方差，从而提高模型的预测性能。

假设我们有一个数据集，其中包含100个房屋的特征和售价。我们希望训练一个回归模型来预测房屋的售价。我们可以使用XGBoost算法，它会使用多个回归树来组成一个集成模型。

在XGBoost中，每个回归树的预测结果可以被看作是对真实值的一个修正。举个例子，假设我们有三个回归树，它们的预测结果分别是：10万美元，-5万美元和2万美元。这些预测结果都是相对于真实值的偏差或误差。如果我们将它们相加起来，得到的结果是7万美元。这意味着我们认为真实售价比三棵树的平均预测值高7万美元。

XGBoost的目标是让每个新的回归树修正前面所有树的误差，最终得到的集成模型能够更准确地预测真实售价。这是通过优化损失函数来实现的，使得在每一轮迭代中加入一个新的树，能够最大程度地减小残差。最终，所有树的预测结果被简单地相加，得到最终的预测结果。

如果XGBoost模型以及训练好，对于上述例子：三棵回归树的平均预测值为2.33万美元，因此我们认为真实售价比这个平均值高7万美元，所以最终的预测值应该是2.33+7=9.33万美元。

Example

我们来看一个简单的例子。

假设我们有一个数据集，其中包含两个特征，即$x_1$和$x_2$，以及一个目标变量$y$。我们的目标是使用这些特征来预测目标变量$y$的值。

我们首先用XGBoost训练一个回归树模型，得到了以下的结果：

第一个回归树预测值：$0.2x_1-0.1x_2+0.3$
第二个回归树预测值：$0.1x_1+0.3x_2-0.2$
第三个回归树预测值：$-0.2x_1+0.1x_2+0.1$

现在我们有一个新的样本，特征值为$x_1=0.5$，$x_2=0.8$，我们要用这个模型来预测该样本的目标变量值$y$。

我们将新样本的特征值带入每个回归树的预测公式中，得到以下结果：

第一个回归树的预测值：$0.2\times 0.5-0.1\times 0.8+0.3=0.22$
第二个回归树的预测值：$0.1\times 0.5+0.3\times 0.8-0.2=0.4$
第三个回归树的预测值：$-0.2\times 0.5+0.1\times 0.8+0.1=-0.03$

最后，我们将三个回归树的预测值相加，得到最终的预测值为$0.22+0.4-0.03=0.59$。

因此，使用这个XGBoost回归树模型，我们对新样本的目标变量$y$的预测值为$0.59$。

Boosted Regression Trees: Training

这个梯度树提升过程可以用一个房屋售价的例子来解释。假设我们有一个包含100个房屋的数据集，其中每个房屋都有一些特征（比如卧室数量、浴室数量、房屋面积等）和一个售价。我们希望训练一个回归模型来预测房屋的售价。

在这个例子中，我们使用梯度树提升算法来训练模型。具体来说，我们首先用所有的数据来拟合第一棵回归树。然后，我们用这棵树对数据进行预测，得到一个初始的预测值。接下来，我们用真实售价减去初始预测值，得到每个房屋的残差。第二棵树会尝试拟合这些残差，而不是直接拟合真实售价。这个过程会一直持续下去，每一次都会用之前的预测值减去真实值，然后将这些残差传递给下一棵树。

通过这种方式，每棵树都在尝试纠正前一棵树的错误。每棵树的预测结果都是基于之前的预测结果进行修正的。这个过程会一直进行下去，直到达到指定的迭代次数或者达到一定的误差阈值。

在每个回归树中，它们试图预测当前预测的残差（预测值和真实值之间的差异），而不是直接预测真实售价。例如，如果我们有一个房屋的真实售价是90万美元，而当前预测值是80万美元，那么这个房屋的残差就是10万美元。下一棵树会尝试拟合这个残差，以便更好地修正当前预测值。

在训练过程中，每棵树都会尝试将当前预测值变得更接近真实值。每棵树的预测结果都是当前预测值的修正值，这些修正值相加起来就是最终的预测结果。

Regularized Regression Trees

这个流程是梯度树提升算法的一个例子，每个树都试图预测当前预测的残差（ˆyi-yi）。也就是说，如果当前的预测是0.8，但实际标签是0.9，那么新的树会试图通过预测0.1来改进当前的预测。

这个算法的目标是不断减少训练误差，每个树都是通过尝试预测之前所有树的残差来实现这一点。只要不是所有的残差都为零，每个树就可以降低训练误差。然而，如果树的深度太深或者树的数量太多，就会出现过拟合的情况。为了限制树的深度，可以添加L0正则化，即停止分裂，如果wL = 0，这样只有在你通过分裂来减少平方误差大于λ0时才会分裂。为了进一步抵抗过拟合，XGBoost还添加了w的L2正则化。

XGBoost Discussion

与传统的决策树不同，XGBoost在训练时不是通过剪枝来防止过拟合，而是先生成一棵完整的决策树，然后再通过L0正则化来对树进行剪枝，去掉对模型预测贡献较小的部分。

相比于传统的决策树算法，XGBoost在训练时的计算代价相同，但是使用了很多技巧来提高计算效率。然而，XGBoost不像随机森林那样可以并行计算，是因为XGBoost的训练过程中，每个回归树的建立是基于之前树的结果的残差，而残差是序列相关的，每棵树的训练都需要前一棵树的结果，因此每个树的训练都是顺序完成的，无法并行化处理。相反，随机森林是通过随机选择特征和数据集来建立多个决策树，各个树之间独立，可以并行计算。

XGBoost中使用的残差起到了类似于AdaBoost中的权重的作用，重点关注于减少具有大残差的样本的误差。

如果使用的是非二次损失（如逻辑回归），XGBoost就无法使用闭合形式的解，因此它使用了二阶泰勒展开来近似非二次损失，从而在维持模型预测准确度的同时保持了最小二乘的效率

Summary

Ensemble方法是将多个基础分类器的预测组合起来，以提高整个模型的预测准确性。其中平均法是将多个基础分类器的预测结果进行平均，这种方法适用于多个基础分类器之间误差互相独立的情况下。Bagging是一种ensemble方法，它将同一个分类器应用于不同的自助样本，以获得多个基础分类器，然后将它们的预测结果组合起来以获得更好的性能。Boosting是另一种ensemble方法，它是一种能够改进训练误差的方法。XGBoost是一种基于回归树的现代Boosting方法，其中每棵树都对前面树的预测结果进行修正。