源自:系统仿真学报
作者:袁国栋 何明 马子玉 张伟士 刘学达, 李伟
摘
要
为防止多智能体集群跟随多个领导者时编队混乱,提出了3种K-means聚类算法,将集群分成与领导者数量相同的社区,社区内的智能体将跟随同一领导者。所提出的3种算法中,算法1适用于智能体分布空间广的场景,系统达到一致性所需时间最短;算法2则适用于智能体分布稀疏的场景,可有效避免智能体碰撞等危险;算法3则大大降低多智能体集群的控制成本,但将会牺牲系统的收敛速度。相较于传统预先对智能体编号,领导-跟随关系固定的方法,本文提出的分簇方法使系统收敛时间更短,且有效应对中途任务变更的情况,可快速分配给智能体新的合适任务。
关键词
多智能体 ; 多领导者 ; K-means ; 编队控制 ; 分簇方法
引 言
在自然界中群体行为是物种常见的生存方式,如协同狩猎的狼群、“人”字迁徙的雁群、结队觅食的鱼群、分工协作的蜂群等等[1-4]。近年来集群的协同控制研究,特别是牵制控制激发了学者的广泛兴趣。与单个智能体独立工作相比,多智能体协同工作将简单的局部规则进化到协调的全局行为,将大大提高系统的运行效率、灵活性和容错能力。
基于智能体集群中是否有领导者和领导者的多少,多智能体一致性问题可分为3类:即无领导一致性问题[5]、单领导的领导-跟随一致性问题[6]和多领导的控制问题[7]。在无领导者集群一致性研究中,文献[8-9]研究了通信时延下的一致性问题,文献[10-11]提出基于事件触发机制实现一致性。单领导者一致性问题,即领导-跟随问题是多智能体领域主要研究方向。文献[12]提出虚拟领导者概念,实现自由状态下和避障条件下的集群一致性。而后文献[13]等提出牵制控制算法,证明集群内仅需若干个智能体接收到领导者运动信息便可实现集群一致性。多领导者的控制问题,则是将整个多智能体系统拆分,实现多个小集群的一致性。文献[14]等假设非同簇的智能体互不交换信息,设计一种不依赖初始状态且收敛时间固定的算法。文献[15]发现集群规模越大,引导全局运动的智能体数量所占比例则越小,且比重越小准确度越高。文献[16]针对固定拓扑的特殊网络中领导者数量冗余的问题,提出领导者最小数目算法。然而目前所做工作中,无人机规模通常小于10个,离数量超过100个的集群仍有较大差距,领导者只引导若干个跟随者,且领导-跟随关系预先确定,未考虑到复杂网络的随机性,距离实际运用与推广仍有很大距离。
社区挖掘算法是发现复杂系统模块结构特性的重要算法[17],在疫情防范、基因调控和预防网络犯罪等领域发挥着重要作用。传统社区挖掘算法包含LPA[18]和HANP[19]等算法,但这些算法不能准确预测网络中社区数量。而在多智能体系统中,领导者的数量一般预先给定且智能体初始位置随机分布,如果预先规定领导-跟随关系,运动过程中易发生碰撞危险。或者领导者与跟随者相距较远,直接影响系统达到一致性所需时间。
本文提出基于K-means聚类算法[20]将集群分割为与领导者数量相同的社区,社区内的智能体将跟随同一领导者。文章共设计3种算法以满足不同场景的需求。实验证明,相较于传统预分配式跟随多个领导者的算法,基于K-means算法更适合一般性拓扑结构的智能体网络。且集群中智能体数量越多,本文所提出的算法效率越高,系统的一致性越稳定。
1 基础理论
1.1

图论
将智能体看作是一个点,存在通信的智能体间用直线连接,则多智能体系统的拓扑结构可用图论知识表示:图G(V, E, A),点集合V={1, 2,⋯, n}代表智能体,边集合E={(i, j)} 代表智能体 i 和 j 之间存在通信。
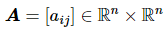
代表邻接矩阵,其中。在无向图 G 一个节点的度被定义为与其直接相连点的个数,即,图的度矩阵则是对角线为各节点度的对角矩阵: 。
Laplacian矩阵被定义为
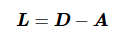
(1)
其谱含有关于图结构特性的信息,最小非零特征值直接反映了图连通的鲁棒性。满足
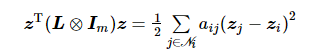
(2)
1.2

K-means算法
K-means作为数据挖掘中的一种无监督聚类算法,实现简单且效果优秀,因而得到了广泛的应用。算法的核心思想是将给定的样本集,按照样本之间的距离远近划分为K个社区。让社区内的点尽量紧密的连在一起,而让社区间的距离尽量的大。在多智能体系统中,K-means算法对如何划分集群使得智能体跟随不同的领导者具有很强的指导作用。设样本集包含n个样本,位置信息为 xi (i=1, 2,…, n),K-means算法的基本流程为:
(1) 随机选取k个初始聚类中心

(3)
(2) 样本i选择距离最近的聚类中心
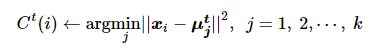
(4)
(3) 重新计算聚类中心
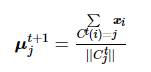
(5)
(4) 重复步骤(2)和(3),直到聚类中心集合 M 发生改变。
设势能函数F(C, x)
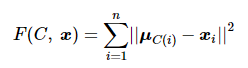
(6)
当聚类中心集合 M 不变时,势能函数F(C, x )达到最小值。但为了防止势能函数长时间不收敛,有时会限制迭代次数或对势能函数设置阈值以降低计算复杂度。
2 基于K-means的多智能体分簇方法
假设由N个独立个体组成的多智能体系统,需要跟随k位领导者。
算法1:基于K-means算法将集群分成k个社区并记录聚类中心位置,领导者选择距离合适的聚类中心,相应社区内的智能体将作为跟随者跟随该领导者。对于领导者如何选择距离合适的聚类中心问题,本文设想两种方法:距离极小极小值法和距离极小极大值法。
假设k个聚类中心位置为M={μ1, μ2,⋯, μk} ,领导者位置信息为pγi, i=1,2,⋯,k 。
距离极小极小法流程为:
(1) 每位领导者选择距离最近的聚类中心并记录具体数值
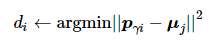
(7)
(2) 设
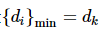
,则领导者pγk 与式(9)中对应的μj 确定关系。
(3) 删除pγk 和μj ,剩余领导者和聚类中心重复步骤(1)和(2)。
而距离极小极大值法则是在步骤(2)中选择
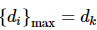
的一对。
实验效果如图1所示,红色代表聚类中心,蓝色则是领导者位置。

图1 领导者和聚类中心之间的关系
如图1(a)中所示,由于距离极小极小值法中领导者优先选用距离最近的聚类中心,这导致后续的领导者无法选择理想的社区,系统总体分配不合理,可能存在某一对相距较大的问题。而距离极小极大值法虽牺牲个别领导者利益,但整体分配更为合理且有效。所以本文将选用距离极大极小值法来帮助选择聚类中心。
算法1实现的分簇如图2所示,其中符号‘☆’表示领导者。由图2可以看出,虽然各个社区之间距离较大,但因为分类过程与领导者无直接关联,所以有时个别领导者出现在另一个社区的范围内。

图2 算法1分簇结果
算法2:直接将k位领导者作为初始聚类中心M0={pγ1, pγ2,⋯, pγk} ,对K-means算法的迭代过程设置上限:
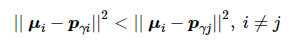
(8)
即领导者始终属于某一固定社区,当该对应关系发生变化时,聚类过程停止,并保留上一次的聚类结果,如图3所示。

图3 算法2分簇结果
从图3可以看出,相较于算法1,算法2所实现的分簇使得社区与领导者之间联系的更为紧密,避免智能体在运动过程中发生碰撞的危险。但社区内部的智能体之间间隔较大,成员分布较为稀疏。
算法3:将互为邻居的智能体间用直线连接,可将多智能体网络分解为多幅子图。文献[13]提出选择子图中某一关键节点作为牵制控制节点,网络中只有牵制控制节点接收到领导者信息,剩余节点则通过局部通信实现逐渐一致。智能体的控制输入ui 重写为
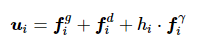
(9)
式中:hi 为牵制控制节点选择项
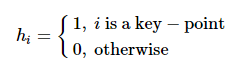
(10)
对牵制控制节点集合使用K-means聚类算法。对于如何选择关键节点问题,文献[21]提出的影响度矩阵既考虑到节点本身的重要性,也考虑到邻居节点的重要程度对它的影响。节点基于影响度矩阵的介数中心性越高,其影响力越大。本实验基于影响度矩阵选择牵制控制节点,并对牵制节点进行聚类分析,结果如图4所示。

图4 算法3分簇结果
从图4可以看出,需要聚类的智能体数减少至初始数量的一半。且智能体初始分布空间越小或智能体数量越多,其网络中子图数量也就越少,算法优势将越大。
3 仿真实验
3.1

实验1
设多智能体系统个体数量N=100,所有个体的初始位置在100 m×100 m的空间内随机分布。智能体感知半径r =6。共有5位领导者,其初始位置和速度信息如表1所示,假设领导者匀速运动。

表1 领导者信息
3种算法中智能体的运动方式相同,差异在于如何确定智能体的领导-跟随关系。以算法3为例,在确定领导-跟随关系后,智能体集群的最终状态如图5所示。从图5可以看出,跟随者成功跟随领导者,未出现碰撞或丢失的情况。

图5 智能体最终分布
智能体的速度变化如图6所示,从图6可以看出,智能体跟随对应的领导者,速度逐渐一致,使得集群整体实现一致性。

3.2 实验2
本实验主要分析3种算法对智能体集群分簇的优劣。其中算法3只对牵制节点聚类,而剩余智能体则靠局部通信跟随牵制智能体,所以将子图中剩余智能体划入牵制节点对应的社区中。假设领导者和智能体集群初始位置随机,k=5,N=100。共选择5组数据,计算势能函数ln(F( Pγ, x )),如表2所示。
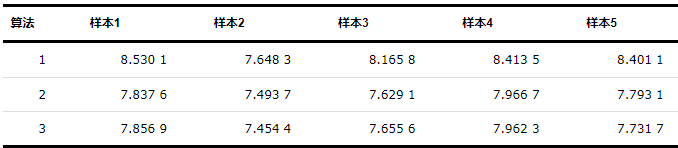
从表2可以看出,算法3和算法2所划分的社区大致相同且要优于算法1,这说明整个网络中存在冗余的信息,而算法3仅对网络中关键节点进行聚类,既保证了足够的精度也降低了计算复杂度。多智能体集群中个体数量越多,算法3优势越大。算法1虽然保证社区内部成员紧密和社区间保持足够距离,但因为领导者与最终聚类中心的位置差异导致领导者作为社区中心时要劣于另外2种算法。
3.3 实验3
本实验主要分析3种算法对系统整体达到一致性所需时间的影响,定义速度差异函数
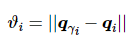
记智能体i与所属领导者γi 保持同步条件
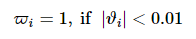
最终系统保持同步条件
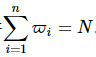
。在实验2的5组样本基础上,系统最终收敛时间如表3所示。
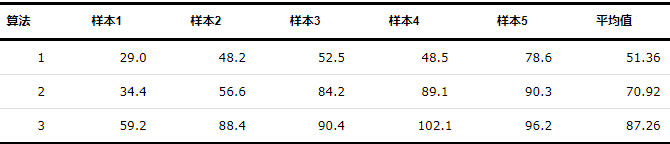
从表3可以看出,算法1由于社区内部智能体间联系的更为紧密,响应速度更快,可以快速实现整个集群的一致性。而算法3相较于其他2种算法,因为只有某些关键智能体可以接收到领导者信息,剩余智能体则通过局部通信与周围智能体保持一致。所以在收敛过程中,有些智能体会出现中途更换领导者的情况,系统总收敛时间较长。
从以上实验可以得出以下结论:
算法1中K-means算法运行完整,因而产生的k个社区彼此间距离大且社区内成员联系更为紧密。但聚类中心不可预测,这导致社区有时距领导者较远。所以算法1更适合智能体分布空间广且需要系统快速实现一致性的场景。
算法2以领导者位置作为初始聚类中心,相较于算法1,社区内智能体与领导者联系的更为紧密,且设置迭代上限,弥补了算法1中最终聚类中心未能均匀分布在领导者周围的不足。算法2更适用于空间小,智能体分布稀疏的场景。
算法3相较于算法1、2,直接参与聚类的智能体数量大大减少,降低了计算复杂度。牵制控制使得仅需少量智能体安装全局控制器,剩余智能体则凭借局部控制器使系统达到一致,更加节约成本,但系统达到一致性所需时间较长。所以在不考虑系统收敛时间,为降低控制成本的条件下,算法3优势更大。
4 结论
本文基于K-means算法解决多智能体集群跟随多个领导者时如何合理分配跟随者的问题。在中途任务变更或任务完成后领取新任务时,本文所提出的算法可跟据新任务重新分配给合适的智能体执行。文中的3种算法各有优劣,其中算法3在吸收前两者优势的基础上,提出牵制控制以引导集群实现一致,极大降低工程难度。集群规模越大,智能体越密集其收敛速度越快。此外本文所做工作主要是提高多领导者的集群规模并将集群初始状态改为随机。目前关于此方向研究较少,所以在横向比较中略显不足。但这也是接下来的研究内容,如何将现有优秀多领导者跟随算法应用于大规模集群并提高收敛速度是未来的主要研究方向。
本文仅用于学习交流,如有侵权,请联系删除 !!
加v“人工智能技术与咨询” 了解更多资讯!!