深度优先搜索DFS
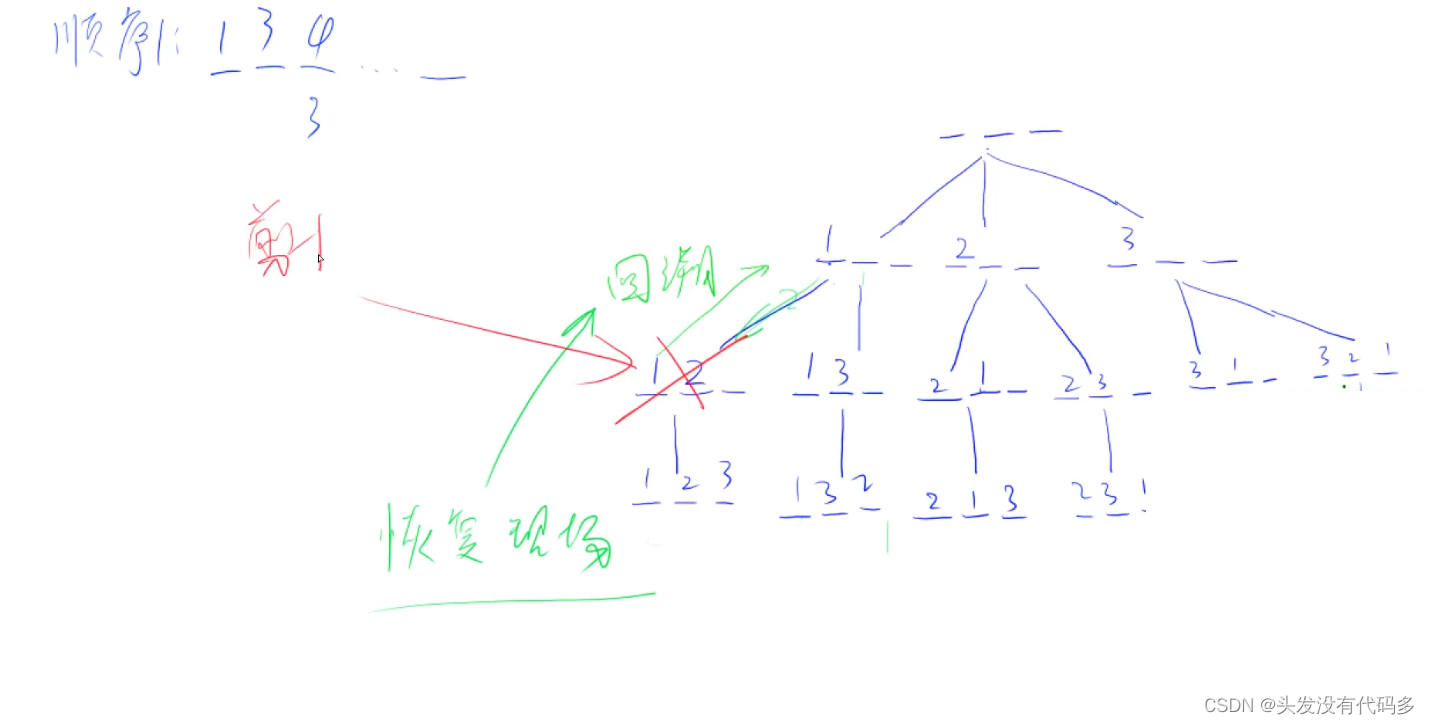
DFS每次往最深处搜,搜到叶子节点就返回,然后继续搜,特点:走到头才返回,返回并不是返回最开始,而是每次返回上一层之后,再看这一层能不能往下搜
DFS有回溯和剪枝。返回上一层的过程叫回溯
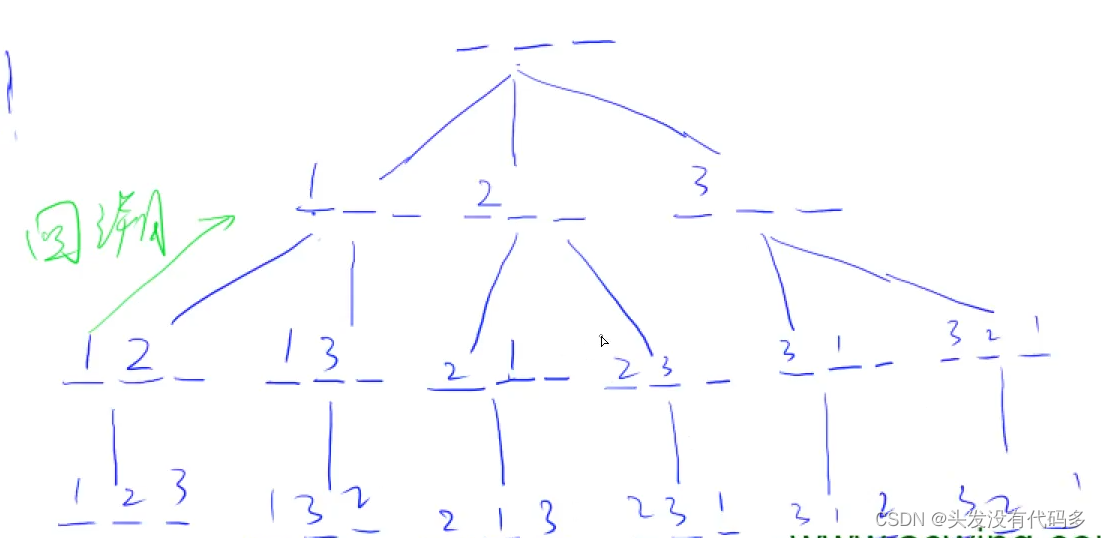
注意回溯的时候要恢复现场
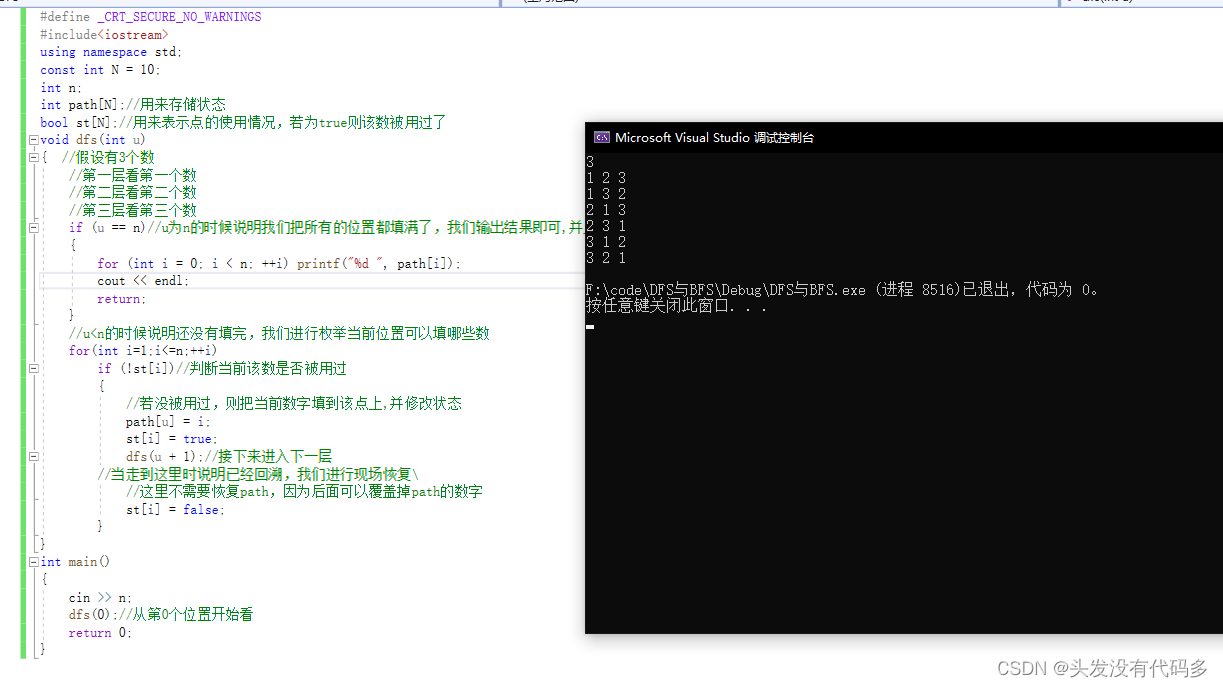
#include<iostream>
using namespace std;
const int N = 10;
int n;
int path[N];//用来存储状态
bool st[N];//用来表示点的使用情况,若为true则该数被用过了
void dfs(int u)
{ //假设有3个数
//第一层看第一个数
//第二层看第二个数
//第三层看第三个数
if (u == n)//u为n的时候说明我们把所有的位置都填满了,我们输出结果即可,并且返回上一层
{
for (int i = 0; i < n; ++i) printf("%d ", path[i]);
cout << endl;
return;
}
//u<n的时候说明还没有填完,我们进行枚举当前位置可以填哪些数
for(int i=1;i<=n;++i)
if (!st[i])//判断当前该数是否被用过
{
//若没被用过,则把当前数字填到该点上,并修改状态
path[u] = i;
st[i] = true;
dfs(u + 1);//接下来进入下一层
//当走到这里时说明已经回溯,我们进行现场恢复\
//这里不需要恢复path,因为后面可以覆盖掉path的数字
st[i] = false;
}
}
int main()
{
cin >> n;
dfs(0);//从第0个位置开始看
return 0;
}n-皇后问题

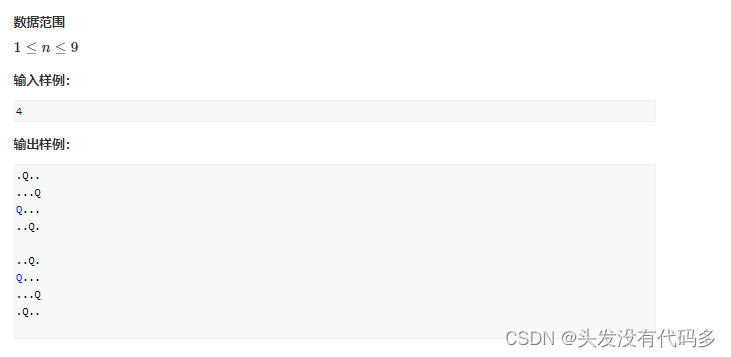
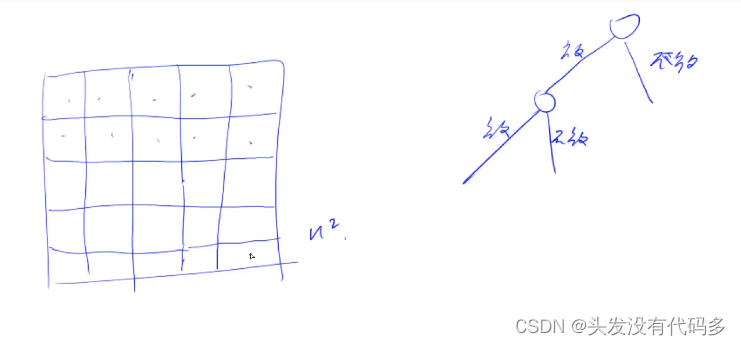
我们可用DFS ,然后加入判断方法即皇后不能处于同一横线,竖线,对角线。若往下走的时候,有某个节点不满足该条件(当该店不满足条件时,我们就没有必要往下搜了),我们把该点剪掉,这就是剪枝
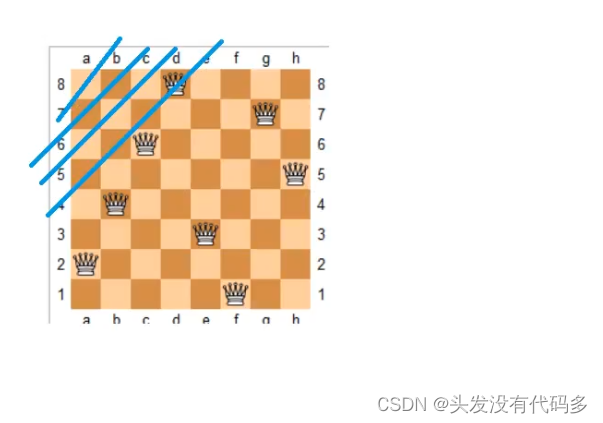
正对角线:从左上角到右下角对角线编号为1-n
反对角线:右上到左下对角线编号为1-n
对角线编号
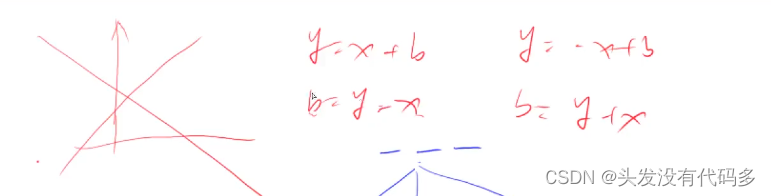
对于b=y-x可能是负数,但是数组下标不可能是负数,因此我们加个偏移量n即可
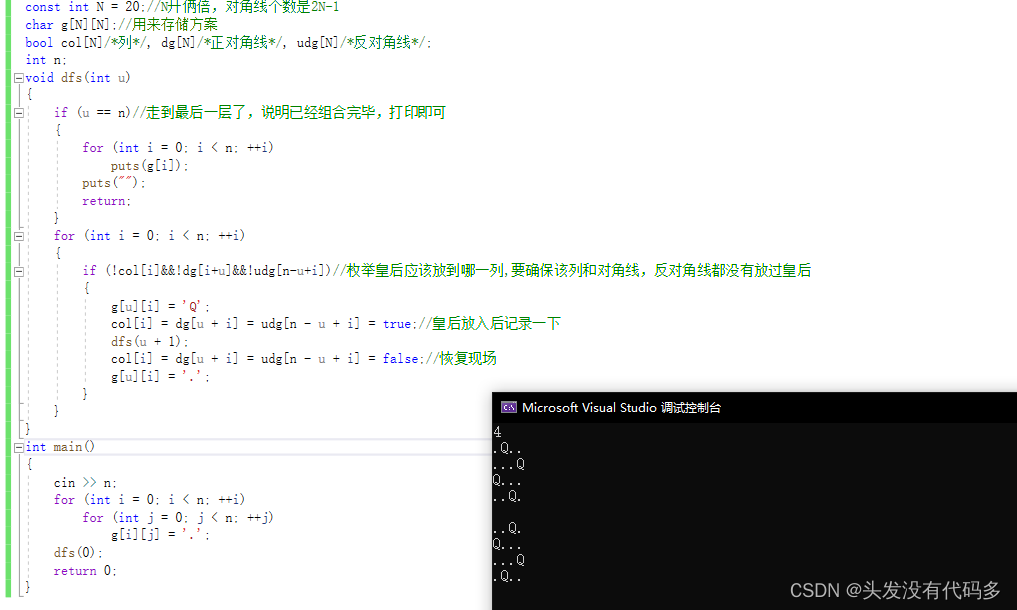
const int N = 20;//N开俩倍,对角线个数是2N-1
char g[N][N];//用来存储方案
bool col[N]/*列*/, dg[N]/*正对角线*/, udg[N]/*反对角线*/;
int n;
void dfs(int u)
{
if (u == n)//走到最后一层了,说明已经组合完毕,打印即可
{
for (int i = 0; i < n; ++i)
puts(g[i]);
puts("");
return;
}
for (int i = 0; i < n; ++i)
{
if (!col[i]&&!dg[i+u]&&!udg[n-u+i])//枚举皇后应该放到哪一列,要确保该列和对角线,反对角线都没有放过皇后
{
g[u][i] = 'Q';
col[i] = dg[u + i] = udg[n - u + i] = true;//皇后放入后记录一下
dfs(u + 1);
col[i] = dg[u + i] = udg[n - u + i] = false;//恢复现场
g[u][i] = '.';
}
}
}
int main()
{
cin >> n;
for (int i = 0; i < n; ++i)
for (int j = 0; j < n; ++j)
g[i][j] = '.';
dfs(0);
return 0;
}方法二
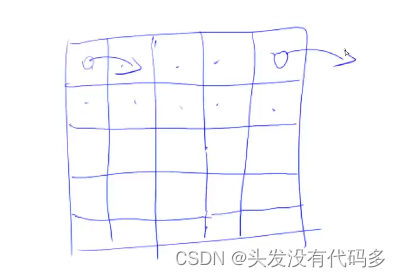
我们以第一个各自为例,第一个格子放是一个分支,第一个格子不放又是一个分支,之后对后面的格子也如此分,当枚举完最后一个格子时,就找到答案了
我们这次让按着格子的顺序横着走
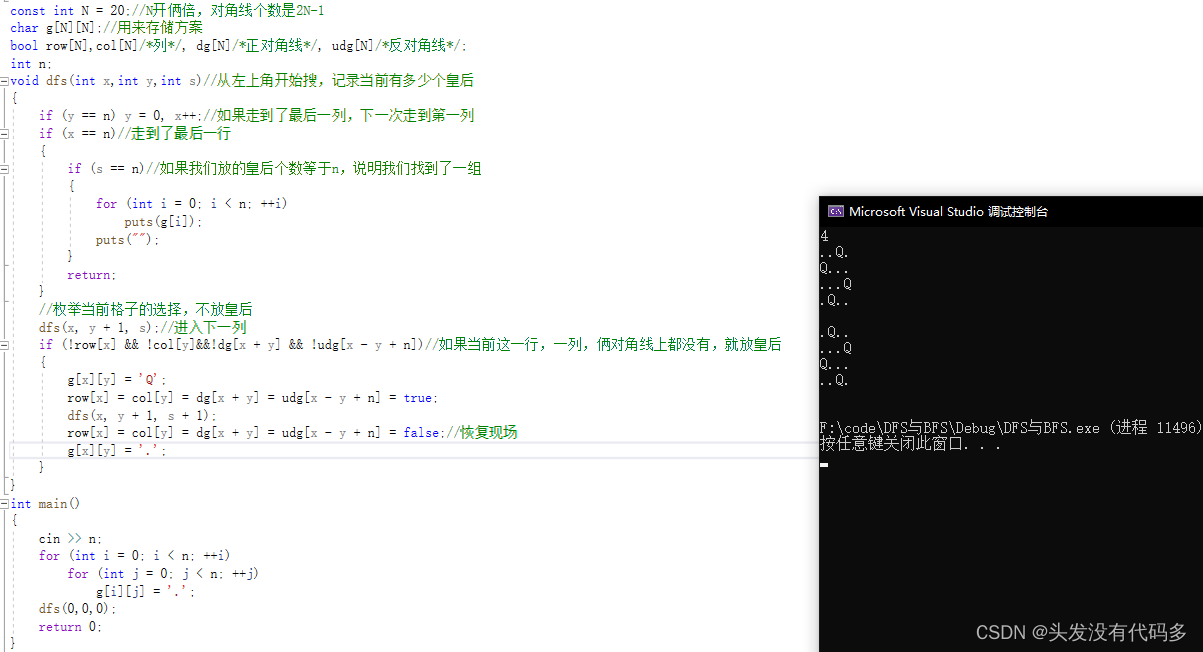
const int N = 20;//N开俩倍,对角线个数是2N-1
char g[N][N];//用来存储方案
bool row[N],col[N]/*列*/, dg[N]/*正对角线*/, udg[N]/*反对角线*/;
int n;
void dfs(int x,int y,int s)//从左上角开始搜,记录当前有多少个皇后,s代表当前皇后的数量,x,y代表坐标
{
if (y == n) y = 0, x++;//如果走到了最后一列,下一次走到第一列
if (x == n)//走到了最后一行
{
if (s == n)//如果我们放的皇后个数等于n,说明我们找到了一组
{
for (int i = 0; i < n; ++i)
puts(g[i]);
puts("");
}
return;
}
//枚举当前格子的选择,不放皇后
dfs(x, y + 1, s);//进入下一列
if (!row[x] && !col[y]&&!dg[x + y] && !udg[x - y + n])//如果当前这一行,一列,俩对角线上都没有,就放皇后
{
g[x][y] = 'Q';
row[x] = col[y] = dg[x + y] = udg[x - y + n] = true;
dfs(x, y + 1, s + 1);
row[x] = col[y] = dg[x + y] = udg[x - y + n] = false;//恢复现场
g[x][y] = '.';
}
}
int main()
{
cin >> n;
for (int i = 0; i < n; ++i)
for (int j = 0; j < n; ++j)
g[i][j] = '.';
dfs(0,0,0);
return 0;
}第二种方式效率较慢
宽度优先搜索BFS
一层一层搜。每层搜完之后去搜下一层。
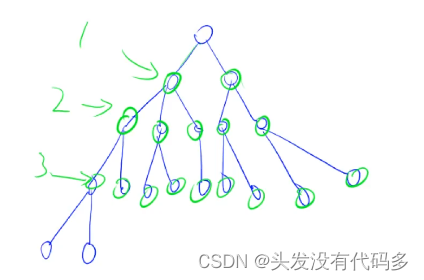

BFS好处:有一个最短路。,而DFS不具有最短性


分别找出所有距离为1,2,3,4,5......n的点
注意BFS是第一次搜到的点才是最短距离,若有点被走过,则不能称为最短距离

点上面的数字代表是第几层被扩展到的,我们可以看到终点上是8,所以起点到终点距离就是8

#include<iostream>
#include<cstring>
#include<algorithm>
#include<queue>//这里使用队列,队列中放的是走的通的点
using namespace std;
typedef pair<int, int> PII;
int n, m;
const int N = 110;
int g[N][N];//存的是原数据
int d[N][N];//存的是每个点到起点的距离(d来存储各个节点到起始节点的路径)
//我们可以用STL队列,也可自己实现队列
PII q[N * N];
int bfs()
{
int hh = 0, tt = 0;//队头和队尾
q[0] = { 0,0 };
memset(d, -1, sizeof d);
d[0][0] = 0;
int dx[4] = { -1,0,1,0 };//在x轴可移动的方向
int dy[4] = {0,1,0,-1};//这里x和y要对应起来表示往前后左右走
while (hh <= tt)
{
auto t = q[hh++];//每次把队头取出来,t是当前坐标
//取出来之后我们利用坐标+-1,尝试往上下左右去找路
//往上走x-1可写作(-1,0)
//,右走(0,1),左走(0,-1),下走(1,0)
for (int i = 0; i < 4; ++i)//枚举4个方向
{
int x = t.first + dx[i], y = t.second + dy[i];//当前坐标的下一个坐标
if (x >= 0 && x < n && y >= 0 && y < m&&g[x][y]==0&&d[x][y]==-1)//如果走完之后在范围内,并且这个点可以走,而且这个点还未被走过
{
d[x][y] = d[t.first][t.second]+1;//如果满足条件,则该点到原点距离等于上一个点到原点距离+1
q[++tt] = { x,y };//该点满足条件时就把该点放入队列当中
}
}
}
return d[n - 1][m - 1];//输出右下角点的距离即可
}
int main()
{
cin >> n >> m;
for (int i = 0; i < n; i++)
for (int j = 0; j < m; j++)
scanf("%d", &g[i][j]);
cout << bfs() << endl;
return 0;
}C++实现
#include <cstring>
#include <iostream>
#include <algorithm>
#include <queue>
using namespace std;
typedef pair<int, int> PII;
const int N = 110;
int n, m;
// 用g来存储图,d来存储各个节点到起始节点的路径
int g[N][N], d[N][N];
int bfs()
{
// 定义一个队列q来存储最新到达的地点,队首出队的时候,也是走向下一个节点的时候
queue<PII> q;
// 将距离d首先初始化为-1
memset(d, -1, sizeof d);
// 初始化起始节点的距离d[0,0] = 0
d[0][0] = 0;
// 将起始节点加到队列中
q.push({0, 0});
// 定义四个方向
int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};
// 如果队列不为空
while (q.size())
{
// 将队首元素赋值给t
auto t = q.front();
// 队首出队
q.pop();
// 站在这个路口,向前后左右四个方向看(这个求向左走(x-1,y)、向右走(x+1,y)、向上走(x,y-1)、向下走(x,y+1)的写法可以背下来)
for (int i = 0; i < 4; i ++ )
{
// t为队首元素,即当前路口的x值,t.first为x轴的值,t.first + dx[i]为向左右走
// t为队首元素,即当前路口的y值,t.second为y轴的值,t.second + dy[i]为向上下走
int x = t.first + dx[i], y = t.second + dy[i];
// 如果如果坐标(x,y)合法(在给定图的范围内)且能走(g[x][y] == 0)且没有走过(d[x][y] == -1)
if (x >= 0 && x < n && y >= 0 && y < m && g[x][y] == 0 && d[x][y] == -1)
{
// 将这个位置(x,y)到起始点(0,0)的距离(在上一步的距离+1(d[t.first][t.second] + 1))加到d[x][y]中
d[x][y] = d[t.first][t.second] + 1;
// 将这个新到达的位置加入队列
q.push({x, y});
}
}
}
// 输出右下角(n-1,m-1)到起始点的距离d[n - 1][m - 1]即可
// 因为bfs有最短性,所有直接输出就是左上角到右下角的最短的路径
return d[n - 1][m - 1];
}
int main()
{
cin >> n >> m;
for (int i = 0; i < n; i ++ )
for (int j = 0; j < m; j ++ )
cin >> g[i][j];
cout << bfs() << endl;
return 0;
}
//再次尝试写
#include<iostream>
#include<queue>
#include<algorithm>
#include<cstring>
const int N = 110;
int g[N][N], d[N][N];
typedef pair<int, int> PII;
int n, m;
queue<PII> A;
int bfs()
{
//上(-1,0) (1,0) (0,-1) (0,1)
int dx[4] = {-1,1,0,0};
int dy[4] = {0,0,-1,1};
memset(d, -1 ,sizeof d);
d[0][0] = { 0 };
A.push({ 0,0 });
while (!A.empty())
{
auto t = A.front();//当前可用坐标
A.pop();
for (int i = 0; i < 4; i++)//for循环主要是用来找当前所在点周围的点是否可走
{
int x =t.first+dx[i] ;
int y = t.second + dy[i];
if (x >= 0 && x < n && y >= 0 && y < m && g[x][y] == 0 && d[x][y] == -1)//若该点可走而且该点是第一次走过
{
d[x][y] = d[t.first][t.second] + 1;//就在上个点距离的基础上把距离+1
A.push({ x,y });//把该可用的点放入队列中
}
}
}
return d[n - 1][m - 1];//返回右下角的距离
}
int main()
{
cin >> n >> m;
for (int i = 0; i < n; i++)
for(int j = 0; j < m; j++)
cin >> g[i][j];
cout << bfs() << endl;
return 0;
}倒着将路径打印出来
#include<iostream>
#include<queue>
#include<algorithm>
#include<cstring>
const int N = 110;
int g[N][N], d[N][N];
typedef pair<int, int> PII;
int n, m;
PII Prev[N][N];//存放路径
queue<PII> A;
int bfs()
{
//上(-1,0) (1,0) (0,-1) (0,1)
int dx[4] = {-1,1,0,0};
int dy[4] = {0,0,-1,1};
memset(d, -1 ,sizeof d);
d[0][0] = { 0 };
A.push({ 0,0 });
while (!A.empty())
{
auto t = A.front();//当前可用坐标
A.pop();
for (int i = 0; i < 4; i++)//for循环主要是用来找当前所在点周围的点是否可走
{
int x =t.first+dx[i] ;
int y = t.second + dy[i];
if (x >= 0 && x < n && y >= 0 && y < m && g[x][y] == 0 && d[x][y] == -1)//若该点可走而且该点是第一次走过
{
d[x][y] = d[t.first][t.second] + 1;//就在上个点距离的基础上把距离+1
Prev[x][y] = t;
A.push({ x,y });//把该可用的点放入队列中
}
}
}
int x = n - 1, y = m - 1;
while (x || y)
{
cout << x << ' ' << y << endl;
auto t = Prev[x][y];
x = t.first, y = t.second;
}
return d[n - 1][m - 1];//返回右下角的距离
}
int main()
{
cin >> n >> m;
for (int i = 0; i < n; i++)
for(int j = 0; j < m; j++)
cin >> g[i][j];
cout << bfs() << endl;
return 0;
}树与图的深度优先遍历
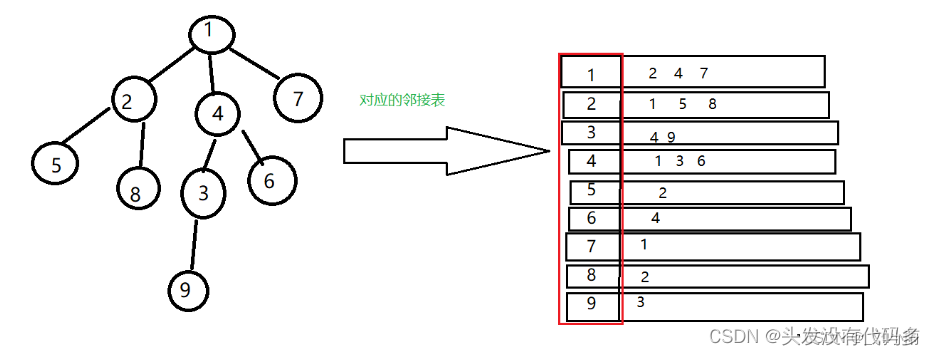
邻接表:为每一个点都开一个单链表
如这里1:1指向到3,1指向4,写作1->3->4 PS:这里3和4谁在前谁在后顺序不重要
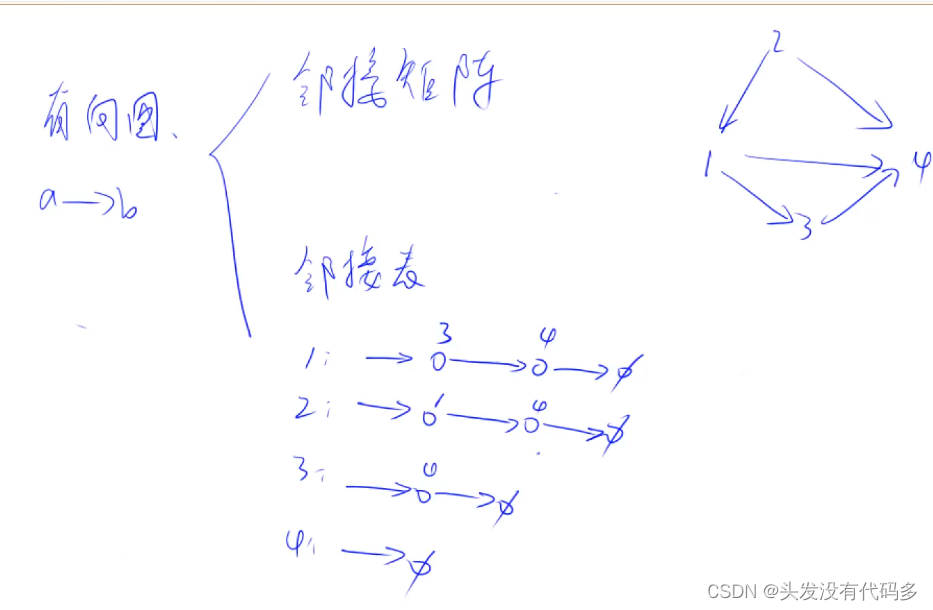
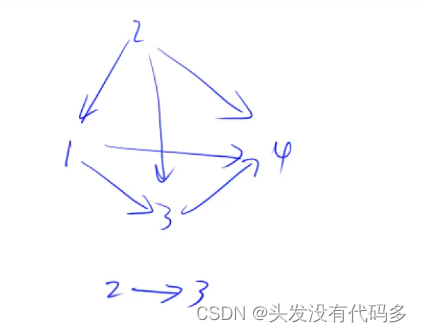
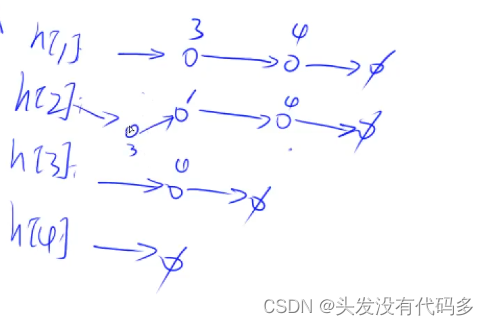
当想插入新的节点如2->3,我们在2对应的单链表中一般选择在头部位置插入
树的重心

深度优先遍历
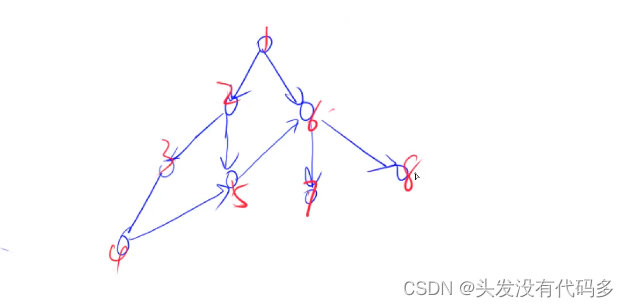
宽度优先遍历顺序
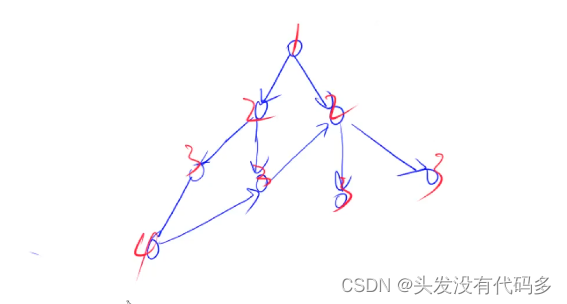
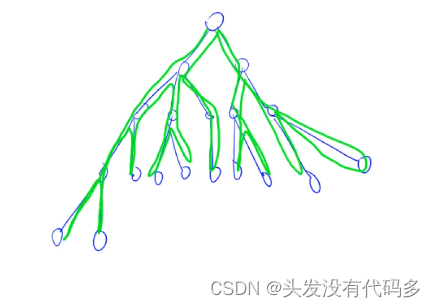
先画出题目给出的树:
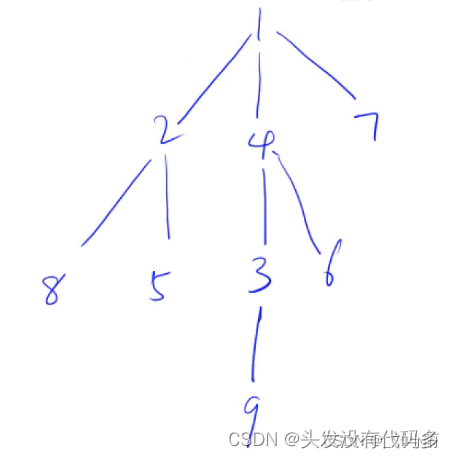
解释一下什么是树的重心
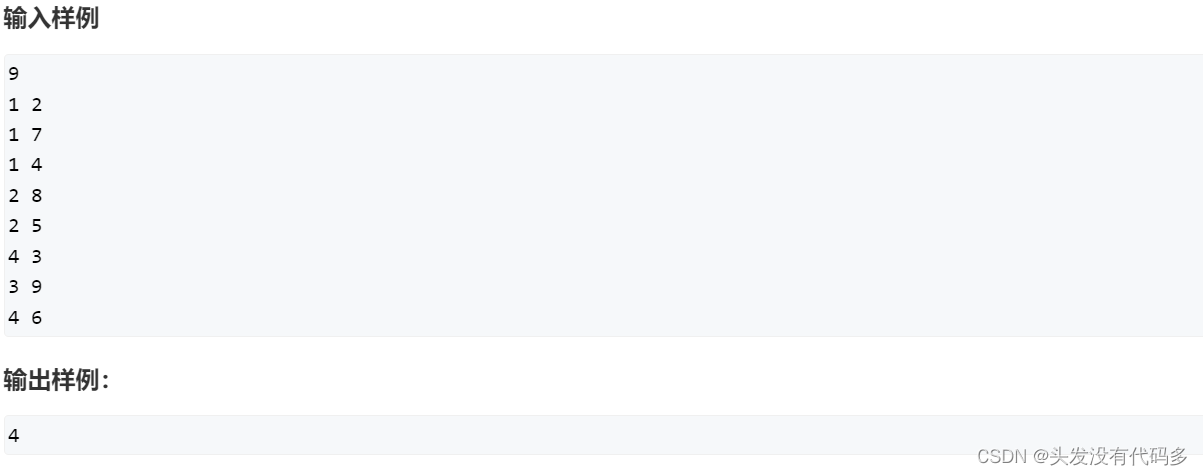
树的重心是指,删除某个结点后剩下的最大连通子树的结点数目最小,如上图是根据样列生成的树
若删除结点1,则剩下三个子树最大的是中间那颗结点有4个,即剩下的最大连通子树的结点数目为4;
若删除结点2,则剩下两个数目为1的子树和一个数目为6的子树,即剩下的最大连通子树的结点数目为6;
若删除结点3,剩下一个数目为1的子树,和一个数目为7的子树,即剩下的最大连通子树的结点数目为7……
枚举可得剩下的最小的最大连通子树的结点数目为4也就是说结点1是树的重心。另外注意题目要求答案是输出剩下的最小的最大连通子树的结点数目。
思路:树的深搜
算出每个结点被删除后剩下的最大连通子树的结点数目,输出最小值即可,那么问题就是怎么求一个结点被删除后的最大连通子树的结点数目,删除一个结点后,剩下的子树可以被分为两个部分,例如删除结点4:
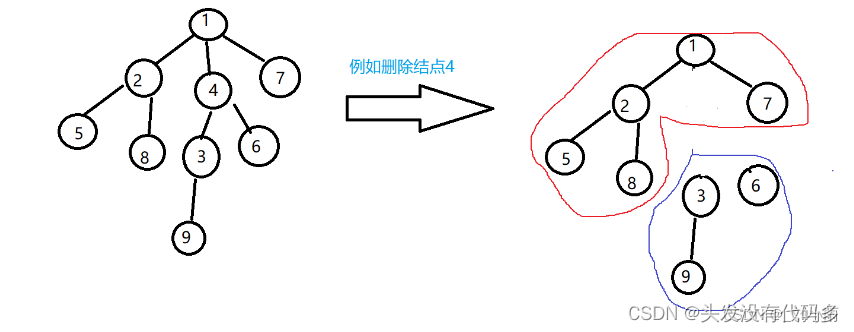
蓝色部分是结点4的子树,红色部分我们暂时称为其他部门,因为我们知道树的总结点数n,只要能算出蓝色部分的数目s,那么其他部分的数目就是n-s
代码如何实现
一是这颗树我们要怎么存储,
二是上述dfs怎么实现
树的存储
首先树是一种特殊的图(无向图),存储图有邻接矩阵法和邻接表法,这里选择邻接表法,另外这里的是无向图,所以存边的时候要存正反两条。
#include<iostream>
#include<algorithm>
#include<cstring>
#include<math.h>
using namespace std;
const int N = 100010,M=N*2;
int h[N];//N个链表的链表头
int e[N];//每个节点的值是多少
int ne[N];//每个节点的next指针是多少
int idx;
bool st[N];//存储被遍历过的点,注意所有的点只被遍历一次,不能出现重复遍历
int ans = N;//记录全局答案
int n;
void add(int a, int b)//a开头的链表中头插b
{
e[idx] = b;
ne[idx] = h[a];
h[a] = idx++;
}
int dfs(int u)//计算以u为根的子树中点的数量
{
st[u] = true;//标记当前这个点已经被搜过了
int sum = 1;//当前这个点也算是一个点,所以sum从1开始, sum用于记录根子树的大小
int res = 0;//存储删除该点后,每个连通块大小的最大值
for (int i = h[u]; i != -1; i = ne[i])//遍历所有的边
{
int j = e[i];//存一下当前链表里面的节点所对应图里面点的编号
if (!st[j])//如果j没有被搜过
{
int s=dfs(j);//我们就继续搜
//用S表示当前子树的大小
res = max(res, s);//当前子树也是一个联通块,和res比一下,取一个最大值
sum += s;
}
}
res = max(res, n - sum);//由于子树上面的部分也要计算,我们取最大值,res存删掉某点后,最大联通块点数
ans = min(ans, res);//取最小值
return sum;
}
int main()
{
cin >> n ;
memset(h, -1, sizeof h);//将所有的头节点初始化为-1
for (int i = 0; i < n-1; i++)
{
int a, b;
cin >> a >> b;
add(a, b), add(b, a);//由于题目是无向边,所以我们加入俩条边
}
dfs(1);//从第一个点开始搜
cout << ans << endl;
return 0;
}树与图的宽度优先遍历
图中点的层次
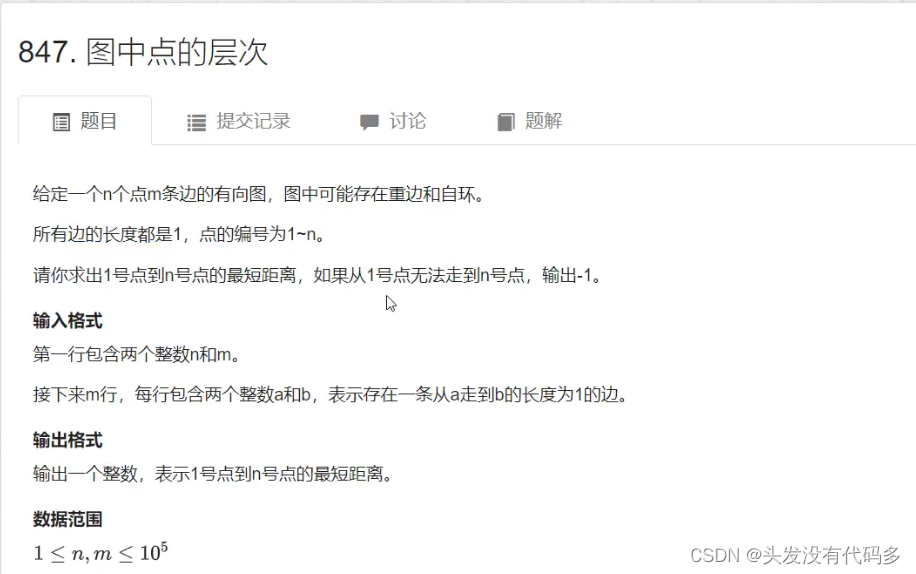
输入样例:
4 5
1 2
2 3
3 4
1 3
1 4
输出样例:
1
基本框架
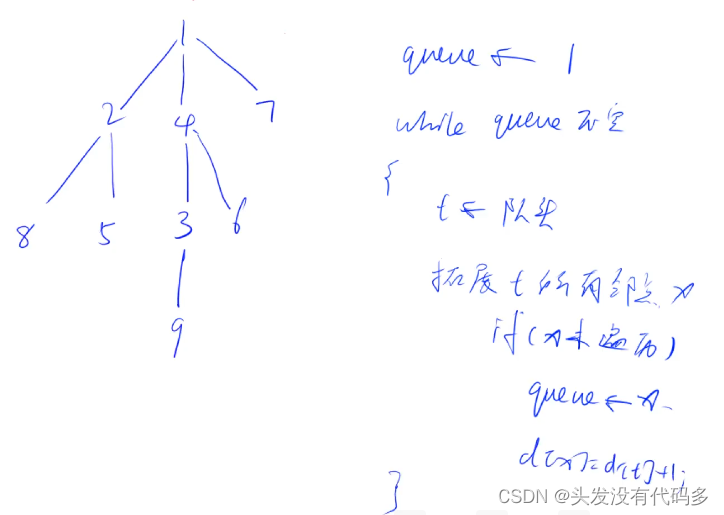
#include<iostream>
#include<cstring>
#include<queue>
using namespace std;
const int N = 100010;
int n, m;
int h[N], e[N], ne[N], idx;
int d[N];//d中存储距离
void add(int a, int b)
{
e[idx] = b;
ne[idx] = h[a];
h[a] = idx++;
}
int bfs()
{
queue<int> A;
A.push(1);
memset(d, -1, sizeof d);
d[1] = 0;
while (A.size())
{
int t = A.front();//取队头
A.pop();
for (int i = h[t]; i != -1; i = ne[i])
{
int j = e[i];
if (d[j] == -1)//如果该点未被遍历过,就入队
{
d[j] = d[t] + 1;
A.push(j);
}
}
}
return d[n];
}
int main()
{
cin >> n >> m;
memset(h, -1, sizeof h);
for (int i = 0; i < m; ++i)
{
int a, b;
cin >> a >> b;
add(a, b);
}
cout << bfs() << endl;
return 0;
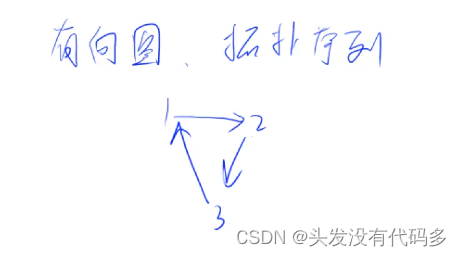
}有向图的拓扑序列
有向图才有拓扑序列,
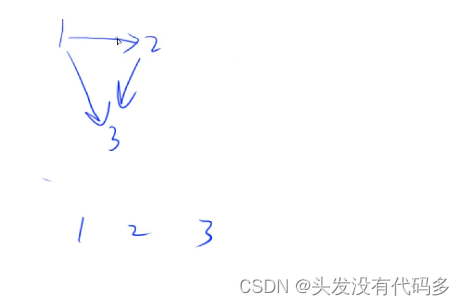
如这里的1,2,3就是拓扑序列,因为1在2前面,2在3前面,1也在3前面。这些关系通过图可以看出。
若一个由图中所有点构成的序列 A 满足:对于图中的每条边 (x,y),x 在 A 中都出现在 y 之前,则称 A 是该图的一个拓扑序列。只要出现环,就不是拓扑序,因为环不能占成x在y前面,有向无环图一定存在拓扑序列,有向无环图也称拓扑图。
入度:有多少条边指向自己。 出度:一个点指向外多少条边
若有点入度为0,意味着没有任何一条边指向该点,因此所有入读为0的点都可以排在最前面的位置。
思路:
把所有入度为0的点入队
进行宽度优先遍历

删掉t->j的出边之后,j的入度-1,如果d[j]=0,就可以让j入队

一个有向无环图,一定至少存在一个入度为0的点
给定一个 n 个点 m 条边的有向图,点的编号是 1 到 n,图中可能存在重边和自环。
请输出任意一个该有向图的拓扑序列,如果拓扑序列不存在,则输出 −1。
若一个由图中所有点构成的序列 A 满足:对于图中的每条边 (x,y),x 在 A 中都出现在 y 之前,则称 A 是该图的一个拓扑序列。
输入格式
第一行包含两个整数 n 和 m。
接下来 m 行,每行包含两个整数 x 和 y,表示存在一条从点 x 到点 y 的有向边 (x,y)。
输出格式
共一行,如果存在拓扑序列,则输出任意一个合法的拓扑序列即可。
否则输出 −1。
数据范围
1 ≤n,m≤10^5
输入样例:
3 3
1 2
2 3
1 3
1234输出样例:
1 2 3#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 100010;
int n, m; // 输入需要的参数n,m
int h[N], e[N], ne[N], idx; // 构建图需要的参数
int d[N]; // d[i] 表示 节点i的入度是多少
int q[N]; // 用q[]来保存保存拓扑序列
// 构建图
void add(int a, int b)
{
e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}
// 拓扑排序
bool topsort()
{
// 用数组模拟队列
int hh = 0, tt = -1;
// 将入度为0的节点放入队列q中
for (int i = 1; i <= n; i ++ )
if (!d[i])
q[ ++ tt] = i;
// 如果队列不为空
while (hh <= tt)
{
// 队首出队,出队元素赋值为t
int t = q[hh ++ ];
// 遍历与出队元素相邻的所有边
for (int i = h[t]; i != -1; i = ne[i])
{
int j = e[i];
if (-- d[j] == 0) // 如果减去一个入度后j节点的入度为0
q[ ++ tt] = j; // 那么将它加到队列中
}
}
// 判断是不是所有下标都入队了,如果tt == n - 1 ,那么队列中就有n个元素
// 那么说明它是一个有向无环图,否则说明它是一个存在环的图,即不存在拓扑序列
return tt == n - 1;
}
int main()
{
scanf("%d%d", &n, &m);
memset(h, -1, sizeof h);
// 构建图
for (int i = 0; i < m; i ++ )
{
int a, b;
scanf("%d%d", &a, &b);
add(a, b);
d[b] ++ ; // 加入一条a指向b的边,b的入度加1,用d[b]++表示b的入度加1
}
// 如果没有拓扑序列输出-1
if (!topsort()) puts("-1");
// 否则输出这个序列
else
{
for (int i = 0; i < n; i ++ ) printf("%d ", q[i]);
}
return 0;
}