一、基础知识

1.浅层神经网络介绍

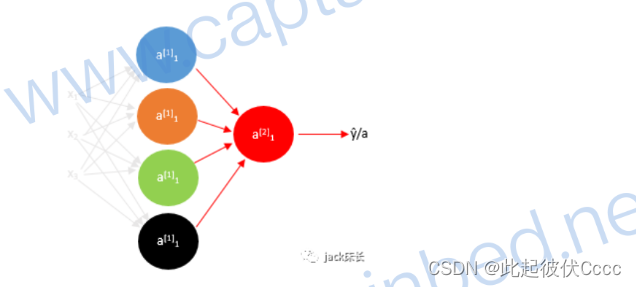
此次构件浅层神经网络，相比于单神经元，浅层神经网络拥有多个神经元，因此又可以称为多神经元网络，如下图所示。
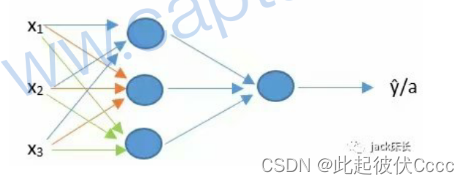
在这里插入图片描述
多神经元网络基本由三部分组成：输入层、隐藏层、输出层
**输入层：**最前面负责输入特征的层（注：在统计神经网络层数时通常不把这一层统计在内，像上图是一个2层的神经网络）。
**隐藏层：**中间的所有层称为隐藏层。
**输出层：**最后一层负责输出最后结果的层。

2.浅层神经网络的正向传播

以下图为例，首先分别计算第一层的每一个神经元的a，其中上标[]里的数字表示第几层，下标数字表示该层中的第几个神经元。
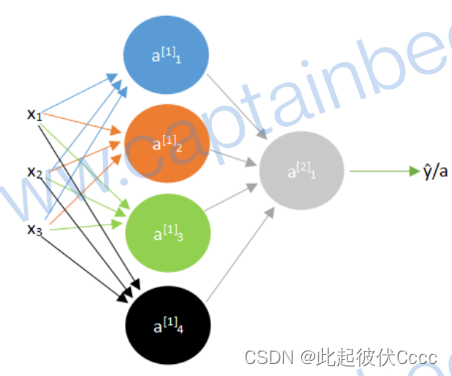
在这里插入图片描述
计算公式如下所示

此例子中的隐藏层的神经元个数为4个，但是当神经元个数较多时需要用向量的形式计算：
第一层：

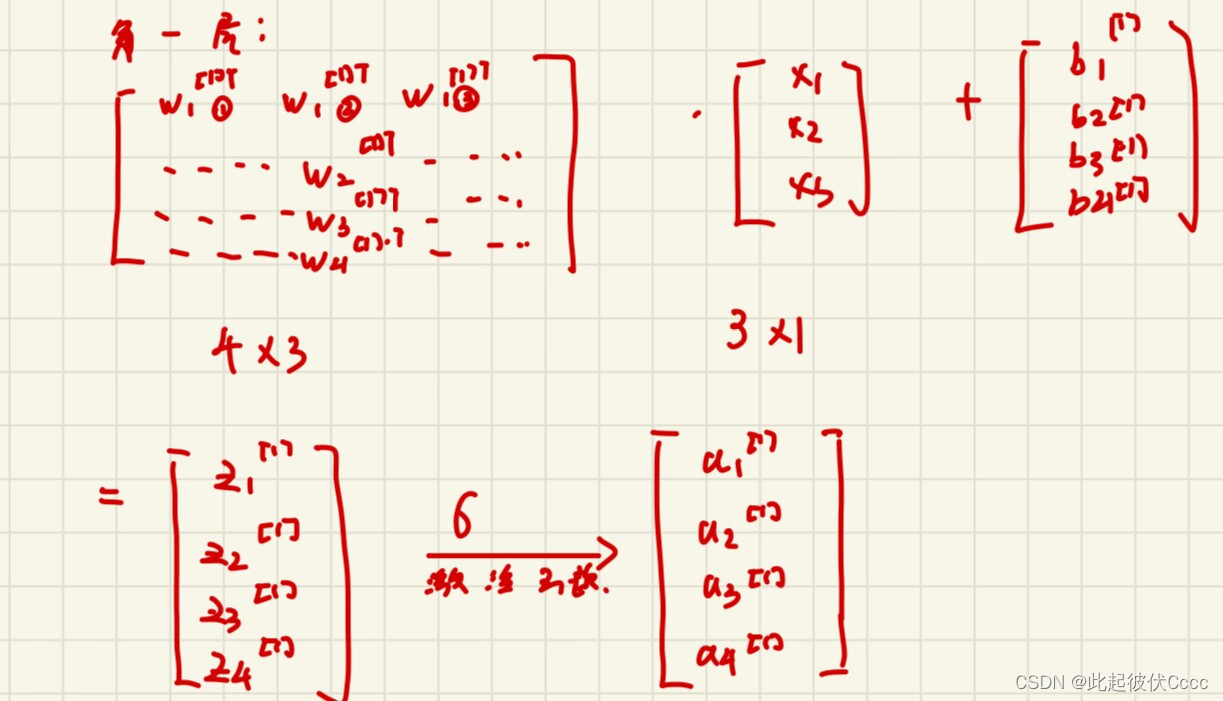
第二层：

此例子中输入为单样本，当进行多样本输入训练时，

由此计算出成本J，完成了依此正向传播。

3.反向传播

在这里插入图片描述
首先计算第二层的相关偏导数，与单神经元网络一致：

之后再计算第一层相关偏导数，由于第一层没有与损失函数直接相邻，只能通过链式法则。计算第一层相关偏导数时，首先需要计算出dZ[1],dW[1],db[1]都可以通过dZ[1]求得。
在这里插入图片描述
之后再进行向量化，最终得到反向传播后计算的相关偏导数如下所示

二、浅层神经网络代码实例

此次实例采用代码生成的虚拟数据集来演示，这个数据集由400个样本组成。这400个样本是400个颜色点。输入特征X是点的横纵坐标，标签Y是点的颜色标签（0表示红色，1表示蓝色）。
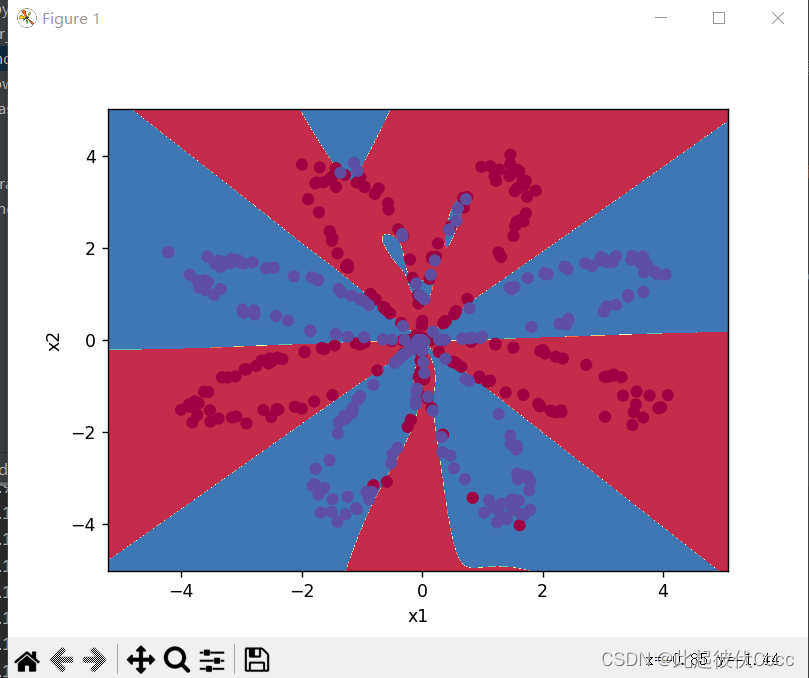
该样本点如下图所示：
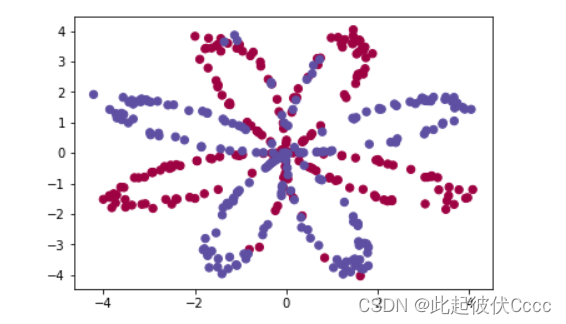
在这里插入图片描述
此次的目标就是通过训练一个神经网络来通过坐标值判断在上图坐标系中某一点可能的颜色，例如坐标（-4，2）的点可能是什么颜色，（-4，3）最可能是什么颜色。将红色和蓝色的点区分出来。

import numpy as np
import matplotlib.pyplot as plt
import sklearn  # 其它库之前我们都介绍过了。这个新库是用于数据挖掘，数据分析和机器学习的库，例如它里面就内置了很多人工智能函数
import sklearn.datasets
import sklearn.linear_model


# 生成数据集函数
def load_planar_dataset():
    np.random.seed(1)
    m = 400  # number of examples
    N = int(m / 2)  # number of points per class
    D = 2  # dimensionality
    X = np.zeros((m, D))  # data matrix where each row is a single example
    Y = np.zeros((m, 1), dtype='uint8')  # labels vector (0 for red, 1 for blue)
    a = 4  # maximum ray of the flower

    for j in range(2):
        ix = range(N * j, N * (j + 1))
        t = np.linspace(j * 3.12, (j + 1) * 3.12, N) + np.random.randn(N) * 0.2  # theta
        r = a * np.sin(4 * t) + np.random.randn(N) * 0.2  # radius
        X[ix] = np.c_[r * np.sin(t), r * np.cos(t)]
        Y[ix] = j

    X = X.T
    Y = Y.T

    return X, Y


# 画图函数
def plot_decision_boundary(model, X, y):
    # Set min and max values and give it some padding
    x_min, x_max = X[0, :].min() - 1, X[0, :].max() + 1
    y_min, y_max = X[1, :].min() - 1, X[1, :].max() + 1
    h = 0.01
    # Generate a grid of points with distance h between them
    xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
    # Predict the function value for the whole grid
    Z = model(np.c_[xx.ravel(), yy.ravel()])
    Z = Z.reshape(xx.shape)
    # Plot the contour and training examples
    plt.contourf(xx, yy, Z, cmap=plt.cm.Spectral)
    plt.ylabel('x2')
    plt.xlabel('x1')
    plt.scatter(X[0, :], X[1, :], c=y, cmap=plt.cm.Spectral)


# 激活函数
def sigmoid(x):
    """
    Compute the sigmoid of x

    Arguments:
    x -- A scalar or numpy array of any size.

    Return:
    s -- sigmoid(x)
    """
    s = 1 / (1 + np.exp(-x))
    return s


# 初始化参数w和b函数
def initialize_parameters(n_x, n_h, n_y):
    """
    参数:
    n_x -- 输入层的神经元个数
    n_h -- 隐藏层的神经元个数
    n_y -- 输出层的神经元个数
    """

    np.random.seed(2)

    # 随机初始化第一层（隐藏层）相关的参数w.
    # 每一个隐藏层神经元都与输入层的每一个神经元相连。每一个相连都会有一个对应的参数w。
    # 所以W1的维度是（n_h, n_x）,表示（隐藏层的神经元个数，输入层神经元个数）
    W1 = np.random.randn(n_h, n_x) * 0.01

    # 将第一层的参数b赋值为0，因为w已经非0了，所以b可以为0
    # 因为每一个神经元只有一个对应的b，所以b1的维度是(n_h, 1)，表示（隐藏层神经元个数，1）
    b1 = np.zeros(shape=(n_h, 1))

    # 同理，初始化第二层的w和b
    W2 = np.random.randn(n_y, n_h) * 0.01
    b2 = np.zeros(shape=(n_y, 1))

    # 将初始化好的参数放入一个字典变量中
    parameters = {"W1": W1,
                  "b1": b1,
                  "W2": W2,
                  "b2": b2}

    return parameters


# 前向传播函数
def forward_propagation(X, parameters):
    """
    参数:
    X -- 输入特征，维度是 (横纵坐标, 样本数)
    parameters -- 参数w和b

    Returns:
    A2 -- The sigmoid output of the second activation
    cache -- a dictionary containing "Z1", "A1", "Z2" and "A2"
    """

    m = X.shape[1]  # 获取样本数
    # print("样本数：" + str(m))

    # 从字典中取出参数
    W1 = parameters['W1']
    b1 = parameters['b1']
    W2 = parameters['W2']
    b2 = parameters['b2']

    # 实现前向传播算法
    Z1 = np.dot(W1, X) + b1
    A1 = np.tanh(Z1)  # 第一层的激活函数我们使用tanh。numpy库里面已经帮我们实现了tanh工具函数
    Z2 = np.dot(W2, A1) + b2
    A2 = sigmoid(Z2)  # 第二层我们使用sigmoid，因为我们要解决的这个问题属于二分问题。这个函数是我们自己在planar_utils里面实现的。

    # 将这些前向传播时得出的值保存起来，因为在后面进行反向传播计算时会用到他们。
    cache = {"Z1": Z1,
             "A1": A1,
             "Z2": Z2,
             "A2": A2}

    return A2, cache


# 这个函数被用来计算成本
def compute_cost(A2, Y, parameters):
    """
    参数:
    A2 -- 神经网络最后一层的输出结果
    Y -- 数据的颜色标签
    """

    m = Y.shape[1]

    logprobs = np.multiply(np.log(A2), Y) + np.multiply((1 - Y), np.log(1 - A2))
    cost = - np.sum(logprobs) / m

    return cost


# 然后就是反向传播
def backward_propagation(parameters, cache, X, Y):
    """
    参数:
    parameters -- 参数w和b
    cache -- 前向传播时保存起来的一些数据
    X -- 输入特征
    Y -- 标签
    """
    m = X.shape[1]  # 获取样本数

    W1 = parameters['W1']
    W2 = parameters['W2']

    A1 = cache['A1']
    A2 = cache['A2']

    # 根据我们文章中介绍的算法公式来计算梯度（偏导数）
    dZ2 = A2 - Y
    dW2 = (1 / m) * np.dot(dZ2, A1.T)
    db2 = (1 / m) * np.sum(dZ2, axis=1, keepdims=True)
    dZ1 = np.multiply(np.dot(W2.T, dZ2), 1 - np.power(A1, 2))
    dW1 = (1 / m) * np.dot(dZ1, X.T)
    db1 = (1 / m) * np.sum(dZ1, axis=1, keepdims=True)

    grads = {"dW1": dW1,
             "db1": db1,
             "dW2": dW2,
             "db2": db2}

    return grads  # 返回计算得到的梯度


# 用上面得到的梯度来进行梯度下降（更新参数w和b，使其更优化）
def update_parameters(parameters, grads, learning_rate=1.2):
    """
    参数:
    parameters -- 参数w和b
    grads -- 梯度
    """

    W1 = parameters['W1']
    b1 = parameters['b1']
    W2 = parameters['W2']
    b2 = parameters['b2']

    dW1 = grads['dW1']
    db1 = grads['db1']
    dW2 = grads['dW2']
    db2 = grads['db2']

    # 根据梯度和学习率来更新参数，使其更优
    W1 = W1 - learning_rate * dW1
    b1 = b1 - learning_rate * db1
    W2 = W2 - learning_rate * dW2
    b2 = b2 - learning_rate * db2

    parameters = {"W1": W1,
                  "b1": b1,
                  "W2": W2,
                  "b2": b2}

    return parameters


# 上面已经将各个所需的功能函数都编写好了。现在我们将它们组合在一个大函数中来构建出一个训练模型。
def nn_model(X, Y, n_h, num_iterations=10000, print_cost=True):
    """
    Arguments:
    X -- 输入特征
    Y -- 标签
    n_h -- 隐藏层的神经元个数
    num_iterations -- 训练多少次
    print_cost -- 是否打印出成本
    """

    np.random.seed(3)
    n_x = X.shape[0]  # 根据输入特征的维度得出输入层的神经元个数
    n_y = Y.shape[0]  # 根据标签的维度得出输出层的神经元个数

    # 初始化参数
    parameters = initialize_parameters(n_x, n_h, n_y)
    W1 = parameters['W1']
    b1 = parameters['b1']
    W2 = parameters['W2']
    b2 = parameters['b2']

    # 在这个循环里进行训练，一次一次地对参数进行优化
    for i in range(0, num_iterations):
        # 进行前向传播
        A2, cache = forward_propagation(X, parameters)

        # 计算出本次的成本
        cost = compute_cost(A2, Y, parameters)

        # 进行反向传播。根据前向传播得到的一些值算出梯度。
        grads = backward_propagation(parameters, cache, X, Y)

        # 根据梯度对参数进行一次优化（下降）
        parameters = update_parameters(parameters, grads)

        # 将本次训练的成本打印出来
        if print_cost and i % 1000 == 0:
            print("在训练%i次后，成本是: %f" % (i, cost))

    return parameters


# 我们已经可以通过上面的函数来进行参数训练。
# 这个函数可以利用上面学习到的参数来对新数据进行预测
def predict(parameters, X):
    """
    参数:
    parameters -- 训练得出的参数（学习到的参数）
    X -- 预测数据
    """

    # 预测其实就是简单地执行一次前向传播
    A2, cache = forward_propagation(X, parameters)
    predictions = np.round(A2)  # 对结果进行四舍五入，小于0.5就是0，否则就是1

    return predictions


np.random.seed(1)  # 设置一个随机数种子，来保证后面我的代码产生的随机数与你们电脑上产生的一样,这样我的结果才能和你们运行的结果一样
X, Y = load_planar_dataset()

# 将训练集送入模型中，并设置隐藏层数为4层，训练次数为1000次
parameters = nn_model(X, Y, n_h=50, num_iterations=20000,print_cost=True)
# 然后用训练得出的参数进行预测。
predictions = predict(parameters, X)
print('预测准确率是: %d' % float((np.dot(Y, predictions.T) + np.dot(1 - Y, 1 - predictions.T)) / float(Y.size) * 100) + '%')
plot_decision_boundary(lambda x: predict(parameters, x.T), X, Y.ravel())
plt.show()