前言

本周阅读文献《Simulate the forecast capacity of a complicated water quality model using the long short-term memory approach》，本文主要研究了LSTM模拟复杂水质模型（即环境流体动力学代码，EFDC）预测能力的能力，通过NSE系数评估LSTM性能，并应用随机森林来确定LSTM性能的关键驱动因素。结果表明，许多LSTM可以达到可接受的性能水平。叶绿素a、水温和总磷被认为是LSTM性能的关键驱动因素，这与湖沼学理论一致，证实了结构简单的LSTM可以模拟EFDC的预测能力。另外，学习了时间序列预测的相关知识，了解了时间序列预测常用的模型。

This week,I read an article which investigates the ability of LSTM to simulate the forecast capacity of a complicated water quality model. The LSTM performances are evaluated by the Nash–Sutcliffe efficiency coefficient, and random forest is applied to identify the key drivers of LSTM performance. The results show that many LSTMs could achieve an acceptable performance level. Chlorophyll a, water temperature, and total phosphorus are identified as the key drivers of LSTM performances, which are consistent with limnological theories. It is thereby confirmed that an LSTM with a simple structure could simulate the forecast capacity of EFDC. Then, I learn the relevant knowledge of time series forecasting and understood the commonly used models for time series forecasting.

文献阅读

题目：Simulate the forecast capacity of a complicated water quality model using the long short-term memory approach
作者：Zhongyao Liang , Rui Zou ，Xing Chen ，Tingyu Ren ，Han Su，Yong Liu

摘要

利用复杂的水质模型是用于预测水质的主要方法。然而，由于数据限制、大量计算和未来边界条件等限制，这些模型不容易使用。长短期记忆（LSTM）可以克服这些限制;然而，它在水质预报中的应用很少被探索。本研究研究了LSTM模拟复杂水质模型（即环境流体动力学代码，EFDC）预测能力的能力。首先，EFDC运行以产生六个水质变量的长期（12年）时间序列。这些变量与嵌入在EFDC中的方程具有内在关联，这些方程表示模拟系统的动态。LSTM的开发是为了使用六个水质变量提前1-31天预测叶绿素的浓度。然后，生成的数据用于训练具有不同模型结构（输入变量的组合、隐藏层数和滞后时间）的多个 LSTM。通过NSE系数评估LSTM性能，并应用随机森林来确定LSTM性能的关键驱动因素。结果表明，许多LSTM可以达到可接受的性能水平。叶绿素a、水温和总磷被认为是LSTM性能的关键驱动因素，这与湖沼学理论一致。隐藏层的数量和滞后时间实际上对 LSTM 性能没有影响。由此证实，结构简单的LSTM可以模拟EFDC的预测能力。结果还表明，本研究中的机制引导LSTM可能捕获某些机制特征。因此，LSTM有望成为水质预报的一种有前途的方法。

简介

水质预报对于提供早期预警和提前采取行动减轻污染至关重要，使用复杂的水质模型，例如环境流体动力学代码（EFDC），是用于预测水质的主要方法，因为这些模型能够描述水质变量的迁移和转变。在实践中，复杂的水质模型的开发总是数据要求高且耗时，此外，水质模型的预测精度在很大程度上取决于边界条件（例如天气条件和负荷输入）的预测。作为替代方案，使用数据驱动的方法可以有效地建立水质变量之间的关系，从而节省计算时间并不需要预测边界条件。然而，人们对它们的直接应用感到担忧，因为数据驱动的方法缺乏机制过程。然而，在数据驱动的方法中缺乏这些过程并不一定导致水质预测的失败。关键问题应该是数据驱动的模型是否可以模拟复杂水质模型的预测能力。如果前一个模型能够，那么即使没有代表任何机制过程的方程，也可以利用数据驱动的方法作为预测水质的有效工具。

本研究有两个研究目标：1）确定LSTM是否能够模拟复杂水质模型的预测能力，2）如果是，确定是否有可能采用简单的模型结构（例如，仅涉及几个输入变量和几个隐藏层的结构）来获得令人满意的模型性能。EFDC是使用最广泛的复杂水质模型之一（Kim等人，2017年，Zou等人，2006年），被选为水质模型。开发了许多LSTM模型，并评估了它们的性能。随机森林（Breiman，2001）进一步用于确定LSTM性能的关键驱动因素，并研究有能力的LSTM是否有可能具有简单的模型结构。

方法

鉴于全球有害藻华的临界条件，叶绿素a（CHL）被选为预测变量（LSTM的响应变量）。至于驱动因素，选择了影响藻类生长的水质变量，例如水温（TEM）和营养物质。此外，预计CHL在某些时间区间内具有紧密的自我关联。相应地选择六个变量作为预测因子：透射电镜、CHL、总磷（TP）、磷酸磷（PO4）、总氮（TN）和氨氮（NH4)。运行EFDC以获得水质变量的12年时间序列，包括预测的响应变量和作为预测因子的几个变量。响应变量和预测变量之间存在复杂的非线性关系。如果 LSTM 能够很好地预测响应变量，那么这证实了它能够模拟 EFDC 的预测容量。其次，开发了许多具有不同模型结构的LSTM。然后根据纳什-萨特克利夫效率系数（NSE）评估它们的性能，通过该系数可以确定LSTM是否能够。最后，基于随机森林（RF）识别模型性能的关键驱动因素，这里选择随机森林是因为它能够确定变量重要性和高预测准确性。RF结果可以帮助确定有能力的LSTM是否具有简单的模型结构。
开发和评估 LSTM
时间 t 处LSTM块的状态图：
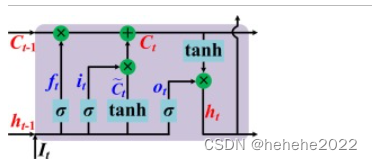
在这里插入图片描述
在本研究中，时间序列分为训练数据集（前9年）和测试数据集（剩余3年）两部分。为了确保输入变量保持在同一尺度上并保证 LSTM 中参数的稳定收敛，所有输入变量和响应都根据方程（9）进行标准化：
在这里插入图片描述
六个水质变量的每个可能组合都可以用作LSTM的输入变量。LSTM 的输入变量组合数为 63 （2⁶–1).设置了 LSTM 的某些超参数，包括与模型结构最相关的隐藏层数和时间滞后。隐藏层的数量和时间滞后会有所不同，以探索它们对模型性能的影响。隐藏层数和时滞都有八种选择：5、10、15、20、30、40、50 和 60。预测天数设置为 1、3、5、…、31。因此，开发的LSTM数量为64 512个（63个×8个×8个×16个）。这些模型是使用训练数据集训练的。
至于LSTM的其他超参数，最大epoch设置为20，这意味着模型将在收敛时结束或epoch达到20。批量大小、验证分数和学习率分别为 5、0.15 和 0.001。通过时间算法的反向传播用于训练LSTM。选择均方根误差作为损失函数。
NSE是模型性能使用最广泛的标准之一,它表示为等式
在这里插入图片描述 基于随机森林RF识别 LSTM 性能的关键驱动因素
随机森林是环境研究中广泛使用的机器学习方法。它由分类或回归树的集合组成。它使用观测值的自举样本来生长每棵树，并且仅使用一小群随机预测变量样本来定义每个节点的拆分。每棵树都长到最大尺寸，无需修剪。最终预测是通过对所有树的结果求平均值来获得的。
在这项研究中，RF用于确定每个预测日LSTM性能的关键驱动因素;总共开发了16个RF。RF 的输入变量包括六个因子变量和两个数值变量（隐藏层数和时间滞后）。因子变量标记是否包括水质变量以预测 LSTM 中的 CHL。对于每个RF，观测值的数量为4032（63×8×8）。

结果

LSTM 的 NSE 值
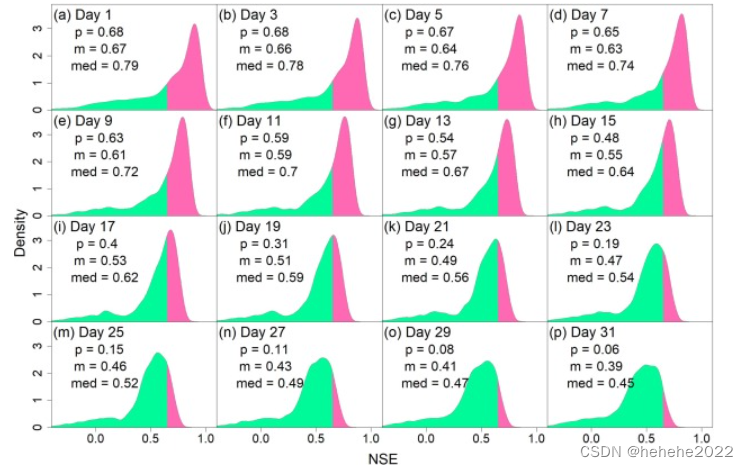
在这里插入图片描述
每个预测日的NSE值分布如图所示。一方面，存在某些大于 0.65 的 NSE 值（LSTM 模型的比例由图中的 p 值表示），这表明存在性能可接受的模型。随着预测天数的增加，NSE峰密度的位置向左移动，整体性能下降，如NSE的平均值和中值（分别为图中的m和med值）所示。
LSTM 性能的关键驱动因素
每个预测日的 RI 结果如图所示。如果相应的 RI 高于 0.1，则 RF 的输入变量被标识为关键驱动因素。对于所有预测日，确定了三个关键驱动因素：包含或不包含CHL，TP和TEM（。对于每个预测日，其他五个输入变量的 RI 总和小于 0.1。注意，两个超参数（隐藏层数和时间滞后）均未标识为关键驱动程序。
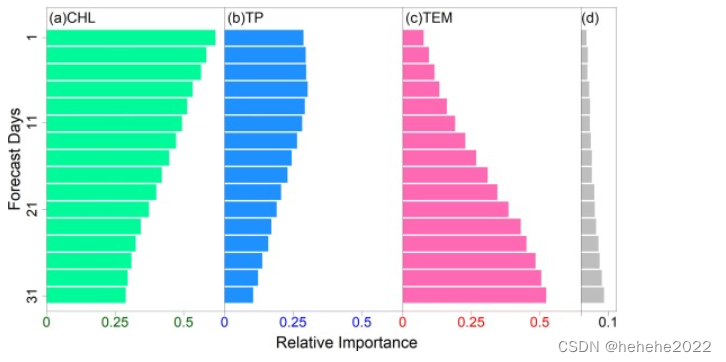
在这里插入图片描述
随着预测天数的增加，三个关键变量的折射率呈现出近似单调的趋势。随着CHL和TP的RI降低，TEM的RI表现出相反的变化。RI 的顺序也会随着预测天数而变化。从第 1 天到第 15 天，三个关键变量的 RI 顺序为 CHL > TP > TEM。在第17天，TEM取代TP的位置，成为第二个重要的驱动因素。第 23 天后，TEM 的 RI 超过 CHL 的 RI，并且 RI 顺序变为 TEM > CHL > TP。

讨论

关键驱动因素的鉴定结果与湖沼学的经典理论一致。CHL的预测取决于当前状态和滞后日的变化。
LSTM 具有简单结构模拟 EFDC 预测容量的能力
根据上述结果，结构简单的LSTM可以模拟EFDC的预测容量。首先，由于许多 LSTM 实现了可接受的性能，因此它们可以很好地模拟 EFDC 的预测容量。其次，只有三个水质变量被确定为LSTM性能的关键变量。这些水质变量始终受到定期监测。这两个超参数（隐藏层数和时间滞后）对 LSTM 性能的影响最小，并且都可以设置为较小的值。因此，具有简单结构的LSTM模型可用于获得高NSE值（图5）。最后，结果与湖沼学理论之间的一致性进一步支持了结果的可靠性。

结论

研究了LSTM模拟EFDC预测容量的能力。结果表明，在 64 512 个 LSTM 中，许多可以达到可接受的性能水平。与湖沼学理论类似，预测CHL所需的关键变量被确定为CHL，TEM和TP。隐藏层的数量和滞后时间可以设置为较小的值。因此，可以验证具有简单结构（例如，只有三个输入变量和五个隐藏层）的LSTM可以模拟EFDC的预测容量。机制引导的LSTM有望成为一种有前途的工具，因为它在预测水质方面既有效又高效。因此，未来的研究应侧重于在进行相对长期的预测时提高模型性能。

时间序列预测学习

1.基础知识

1.1什么是时间序列？

时间序列（英语：time series）是一组按照时间发生先后顺序进行排列的数据点序列。通常一组时间序列的时间间隔为一恒定值（如1秒，5分钟，12小时，7天，1年），因此时间序列可以作为离散时间数据进行分析处理。

时间序列分类
分为：平稳时间序列和非平稳时间序列
平稳时间序列，一般情况下围绕某一个值进行上下波动，无明显的趋势性。

非平稳时间序列，一般指时间序列中包含其他成分，比如趋势性，周期性，季节性和不规则性等。对于不平稳的时间序列一般进行差分处理。

1.2时间序列的基本任务？

单指标时序预测任务：给定某一个指标的历史变化情况，预测其在未来一段时间内的变化。
多指标时序预测任务：给定某几个指标的历史变化情况，预测其在未来一段时间内的变化。该任务与单指标时序预测任务的区别在于，几个指标之间不一定相互独立，而是存在某种影响。
时序异常检测任务：从正常的时间序列中识别不正常的事件或行为的过程。可以从历史数据中检测，也可以基于时序预测对尚未发生的异常做出预警。
时序指标聚类：将变化趋势类似的时序指标归至同一类别。在实际运维工作中，面对的指标可能成百上千，分别对其进行分析，工作量太大，可以在聚类的基础上再做建模分析。
指标关联分析：即分析指标A是否会对指标B有影响，以及有什么样的影响（正向/负向、先后关系、多少时间步后造成影响等等）。

平稳性

平稳性是时间序列中最重要的概念之一。一个平稳的序列意味着它的均值、方差和协方差不随时间变化。大多数的时间序列模型都假设时间序列（TS）是平稳的。首先，我们可以说，如果一个TS在一段时间内有一个特定的行为，那么它很有可能在将来遵循相同的行为。与非平稳序列相比，平稳序列的相关理论更为成熟，更易于实现。
平稳性的检验方法
ACF
平稳序列的自相关函数(Autocorrelation function，ACF)与任何特定时间 t无关，是时间间隔h 的函数，用于测量时间序列滞后值之间的线性关系,以 ρh 表示：
在这里插入图片描述

其中 h 是时间间隔。自相关系数是相关系数的一种，描述变量序列与自身间隔时间 h 的序列的相关性。协方差描述一个变量随另一个变量变化的程度。不同于统计学中常见的相关性分析假设变量间相互独立，自相关分析的对象是同一个变量的不同时间的值，因此， Xt 与 Xt+h 间会存在依赖。

假设检验: 常用的用于检测平稳性的假设检验是ADF（Augmented Dickey-Fuller Test）检验，p值小于0.05便可以认为平稳。
平稳性转换方法
给定一个非平稳的时间序列，一般需要将它转换为平稳序列，再做建模。常用的平稳性转换方法如下：

变形（log函数等）
减去移动平均、指数平均等
差分

所谓差分，就是用 xt - xt-1 的值代替xt, 这是一阶差分。在一阶差分的基础上，继续做差分，就是二阶差分。对于大部分时序数据来说，二阶差分后，都可以得到平稳序列，很少用到更高阶的差分。对于很多时序预测模型尤其是深度学习模型来说，我们会发现，代码中可能并没有平稳性转换这一步。这是因为这些模型中往往有自动特征提取的步骤，从而隐性地完成平稳性转换。
评价指标

RMSE：均方根误差，最常见的一种。
MAE：平均绝对误差。
MAPE：平均绝对百分比误差。
MASE：平均绝对比例误差，这个用得不多。
R-square：小于0很差，等于0相当于将结果预测为均值，等于1则完全预测正确。这个也比较常见。
Adjusted R-square：消除了R-square中样本数量的影响。

2.时间序列预测

时间序列预测做的就是通过多种维度的数据本身内在与时间的关联特性，利用历史的数据预测未来。

算法汇总

时序预测从不同角度看有不同分类：

从实现原理的角度，可以分为传统统计学，机器学习（又分非深度学习和深度学习）。
按预测步长区分，可以分为单步预测和多步预测，简单来说就是一次预测未来一个时间单元还是一次预测未来多个时间单元的区别。
按输入变量区分，可以分为自回归预测和使用协变量进行预测，区别在于维度中是否含有协变量，例如预测未来销售量时，如果只接受时间和历史销售量数据，则是自回归预测，如果可以接受天气、经济指数、政策事件分类等其他相关变量（称为协变量），则称为使用协变量进行预测。
按输出结果区分，可以分为点预测和概率预测，很多模型只提供了点预测而不提供概率预测，点预测模型后再加蒙特卡洛模拟（或其他转化为概率预测的方式）往往不能准确反映模型输出的预测概念，而在大多数场景下，概率预测更贴近事实情况，对于未来的预测本身就应该是一种概率分布。
按目标个数区分，可以分为一元、多元、多重时间序列预测。举例理解，使用历史的销售量预测未来1天的销售量为一元时间序列预测，使用历史的进店人数、销售量、退货量预测未来1天的进店人数、销售量、退货量（预测目标有三个）为多元时间序列预测，使用历史的红烧牛肉面、酸菜牛肉面、海鲜面的销售量预测未来1天的红烧牛肉面、酸菜牛肉面、海鲜面的销售量（预测目标有三种）为多重时间序列预测。

传统经典时间序列预测的方法有ARIMA（一种非常流行的时间序列预测统计方法，它是自回归综合移动平均（Auto-Regressive Integrated Moving Averages）的首字母缩写），Holt-Winters（是一种（三次）指数平滑方法，Holt (1957) 和 Winters (1960) 将Holt方法进行拓展用来捕获季节因素）；机器学习模型方法，这类方法以lightgbm、xgboost为代表，这类方法一般就是把时序问题转换为监督学习，通过特征工程和机器学习方法去预测；这种模型可以解决绝大多数的复杂的时序预测模型。支持复杂的数据建模，支持多变量协同回归，支持非线性问题。不过这种方法需要较为复杂的人工特征过程部分，特征工程需要一定的专业知识或者丰富的想象力。特征工程能力的高低往往决定了机器学习的上限，而机器学习方法只是尽可能的逼近这个上限。特征建立好之后，就可以直接套用树模型算法lightgbm/xgboost，这两个模型是十分常见的快速成模方法；深度学习类的方法包括Seq2Seq类，比如RNN、LSTM、DeepAR等，Attention类，如Transformer、Informer、TFT等。

深度学习中的LSTM/GRU模型，就是专门为解决时间序列问题而设计的；但是CNN模型是本来解决图像问题的，但是经过演变和发展，也可以用来解决时间序列问题。总体来说，深度学习类模型主要有以下特点：

不能包括缺失值，必须要填充缺失值，否则会报错；
支持特征交叉，如二阶交叉，高阶交叉等；
需要embedding层处理category变量，可以直接学习到离散特征的语义变量，并表征其相对关系；
数据量小的时候，模型效果不如树方法；但是数据量巨大的时候，神经网络会有更好的表现；
神经网络模型支持在线训练。

LSTM学习

LSTM基础知识的学习参考 https://zhuanlan.zhihu.com/p/104475016
模型的基本架构：

class LSTM(nn.Module):
    def __init__(self, input_size=1, hidden_layer_size=100, output_size=1):
        super().__init__()
        self.hidden_layer_size = hidden_layer_size

        self.lstm = nn.LSTM(input_size, hidden_layer_size)

        self.linear = nn.Linear(hidden_layer_size, output_size)

        self.hidden_cell = (torch.zeros(1,1,self.hidden_layer_size),
                            torch.zeros(1,1,self.hidden_layer_size)) # (num_layers * num_directions, batch_size, hidden_size)

    def forward(self, input_seq):
        lstm_out, self.hidden_cell = self.lstm(input_seq.view(len(input_seq) ,1, -1), self.hidden_cell)
        predictions = self.linear(lstm_out.view(len(input_seq), -1))
        return predictions[-1]