本文首发自「慕课网」,想了解更多IT干货内容,程序员圈内热闻,欢迎关注"慕课网"!
原作者:s09g|慕课网讲师
我们知道面对同一道问题时可能有多种解决方案。自然地,我们会将多种方法进行比较。那么怎么样才能知道是A方法好,还是B方法好?这时候我们就需要对算法的复杂度进行分析。
这次我们介绍两个概念:时间复杂度与空间复杂度。并且用Two Sum作为案例,用时间空间复杂度分析Two Sum的三种解法。
时间复杂度
时间复杂度描述的是算法执行需要消耗的时间。同等条件下,消耗时间越少,算法性能越好。但是,算法执行的确切时间无法直接测量,通常只有在实际运行时才能知道。所以我们通过估算算法代码的方法来得到算法的时间复杂度。
空间复杂度
空间复杂度描述的是算法在执行过程中所消耗的存储空间(内存+外存)。同等条件下,消耗空间资源越少,算法性能越好。
大O符号
大O符号是用于描述函数渐近行为的数学符号,在分析算法效率的时候非常有用。
借用wikipedia上的一个例子,解决一个规模为n的问题所花费的时间可以表示为:T(n)=4n2+2n+1。当n增大时,n2项将开始占主导地位,而其他各项可以被忽略。比如当n=500,4n2项是2n项的1000倍大,因此在大多数场合下,省略后者对表达式的值的影响将是可以忽略不计的。
长远来看,如果我们与任一其他级的表达式比较,n2项的系数也是无关紧要的。例如:一个包含n2项的表达式,即使T(n)=1,000,000n2,假定U(n)=n3,一旦n增长到大于1,000,000,后者就会一直超越前者。
案例:Two Sum
给出一个整数数组nums和一个target整数,返回两个和为target的整数。
假定我们正在面试,让我们用面试的方法来分析一下这道题。
1.向面试官确认输入、输出
通过询问面试官,我们可以知道:输入是一个int类型的数组和一个target;返回值是两个下标,并且以数组的形式返回;方法名没有特殊要求。这样一下我们就确定了函数的签名
public int[] twoSum(int[] nums, int target) {
// Solution
}
2.向面试官确认输入、输出是否有特例
接下来我们要确认一下输入输出的细节
- 输入是否可以为空?
- 输入的数组范围是正整数,还是任意范围?
- 输入数组会不会特别大,甚至无法载入内存,比如300GB的数据量?
- 如果输入不合法或者没有正确答案,我们已经返回空数组还是抛出异常?
- 输入的数组中有重复么?如果没有重复,可以同一个数字用两次么?
- 如果有多个解,那么返回第一个,还是所有解?
- 你希望答案写成class,还是只提供方法本身即可?
- ……
有些问题即使题目中已经提到,最好还是再次向面试官确认。如果以上这些问题你没有想到的话,那么说明思路仅限于做题,缺乏面试的沟通技巧。可以多找小伙伴Mock面试,注意多交流。
假设面试官告诉我们:只需要写函数本身。输入数组可能为空,但不会大到无法读进内存。数字的范围就是int类型的范围,可能有重复。对于不合法或者没有正确答案的情况,请自行判断。多个解法是,返回任意一个答案都可以。
得到了这些信息,我们可以先进行防御性编程。
public int[] twoSum(int[] nums, int target) {
if (nums == null || nums.length < 2) {
return new int[0];
}
// TODO: solution here
return new int[0];
}
3.举几个例子
接下来,我们可以要求面试官举几个例子,或者自己提出几个例子,来确保双方对题目没有异议。
Example 1:
Input: nums = [], target = 0
Output: []
Example 2:
Input: nums = [2], target = 4
Output: []
Example 3:
Input: nums = [2, 3, 4, 2], target = 6
Output: [2, 4] or [4, 2]
Example 4:
Input: nums = [2, 7, 11, -2], target = 9
Output: [2, 7] or [7, 2] or [11, -2] or [-2, 11]
- 根据例子1、2,确定没有正确解时返回空数组。
- 根据例子2,确定数字不可重复使用。
- 根据例子3、4,确定如果有多个合适的解,返回任意一个都可以。
- 开始解题
完成了之前的步骤,需要找到正确的思路。这道题有三种思路,我们需要一一分析判断,找到合适的解法之后,和面试官进行讨论。得到面试官的允许之后,才可以开始写代码。(如果一上来就埋头解题,即使做对了也不能拿到最高评价。)
解法1 Brute Force
没有具体思路的时候,暴力破解法应该是第一个想法。几乎任何后续更高效的算法都是在暴力破解法的基础上优化而来的。即使无法优化成功,一个可行解也好过一个高效但不可行的算法。
对于Two Sum这道题,最直观的想法大概是找到所有可能的数字组合,挨个计算他们的和,返回第一个满足条件的组合。这种解法并没有什么技术含量,但是可以作为我们下一步优化的基础。
public int[] twoSum(int[] nums, int target) {
if (nums == null || nums.length < 2) {
return new int[0];
}
for (int i = 0; i < nums.length; i++) { // O(N)
int firstNum = nums[i]; // 确定第一个可能的数字
for (int j = i + 1; j < nums.length; j++) { // O(N)
int secondNum = nums[j]; // 确定第二个可能的数字
if (firstNum + secondNum == target) {
return new int[]{firstNum, secondNum};
}
}
}
return new int[0];
}
假设我们的输入大小为N(即nums的长度为N),for循环遍历每个数字时,假设每访问一个数字需要消耗的1个单位的时间,那么对于长度为N的数组,一共需要消耗N的时间。在计算机领域,我们使用大O记号来表示这种量化方法,将for循环的消耗记为O(N)。由于解法1中,我们使用了嵌套了两重for循环,这说明我们对于N个数字,每个数字除了消耗1个单位时间用于访问,还消耗了N个时间第二次遍历数组,总体的时间消耗为O(N2).
解法2 使用HashSet
反思解法1的步骤,我们利用了两重for循环。第一层for循环我们有不得不使用的理由:因为我们至少需要遍历每个数字。第二个for循环的目的是找到与firstNum相加等于target的数字,在这里我们又使用了for循环。如果有一种办法能够让我们记住已经见过的数字,并且在O(1)的时间内检查是否有数字与firstNum相加等于taget,那么就可以省下一个O(N)的for循环。
有一个已知的数据结构可以解决这个问题——Set。Set对应数学意义上的集合,每个元素在集合中只出现一次,Set提供了add/remove/contains … 等API,并且非常高效消耗均为O(1)。
在遍历数组的过程中,每遇到一个新的数字num,计算target - num的值并记为potentialMatch。检查set中是否包含potentialMatch,如果包含说明存在这么一组数字对,他们的和等于target;如果不包含,那么将当前的num加入set,然后检查下一个数字。
public int[] towSum(int[] nums, int target) {
Set<Integer> set = new HashSet<>();
for (int num : nums) { // O(N)
int potentialMatch = target - num;
if (set.contains(potentialMatch)) { // O(1)
return new int[]{potentialMatch, num};
} else {
set.add(num); // 空间消耗增加O(1)
}
}
return new int[0];
}
这个方法利用了Set的特性:以O(1)的速度快速查询元素是否存在。从而省去了一个for循环,将时间复杂度降到了O(N)。但是Set消耗了额外的空间,在最差的情况下,Set可能保存了每一个数字但依旧返回了空数组。所以,解法二消耗了O(N)的空间和O(N)的时间。
解法3 使用排序
解法2利用了O(N)的额外空间去记录已经访问过的数组。那么是否存在一种办法可以不消耗额外的空间,同时提供高效地查询。
当然没有这种好事?……
除非我们做一步预处理:将输入的数组排序处理。比如下图的例子:nums = [2, 4, 9, 7, 1], target = 6
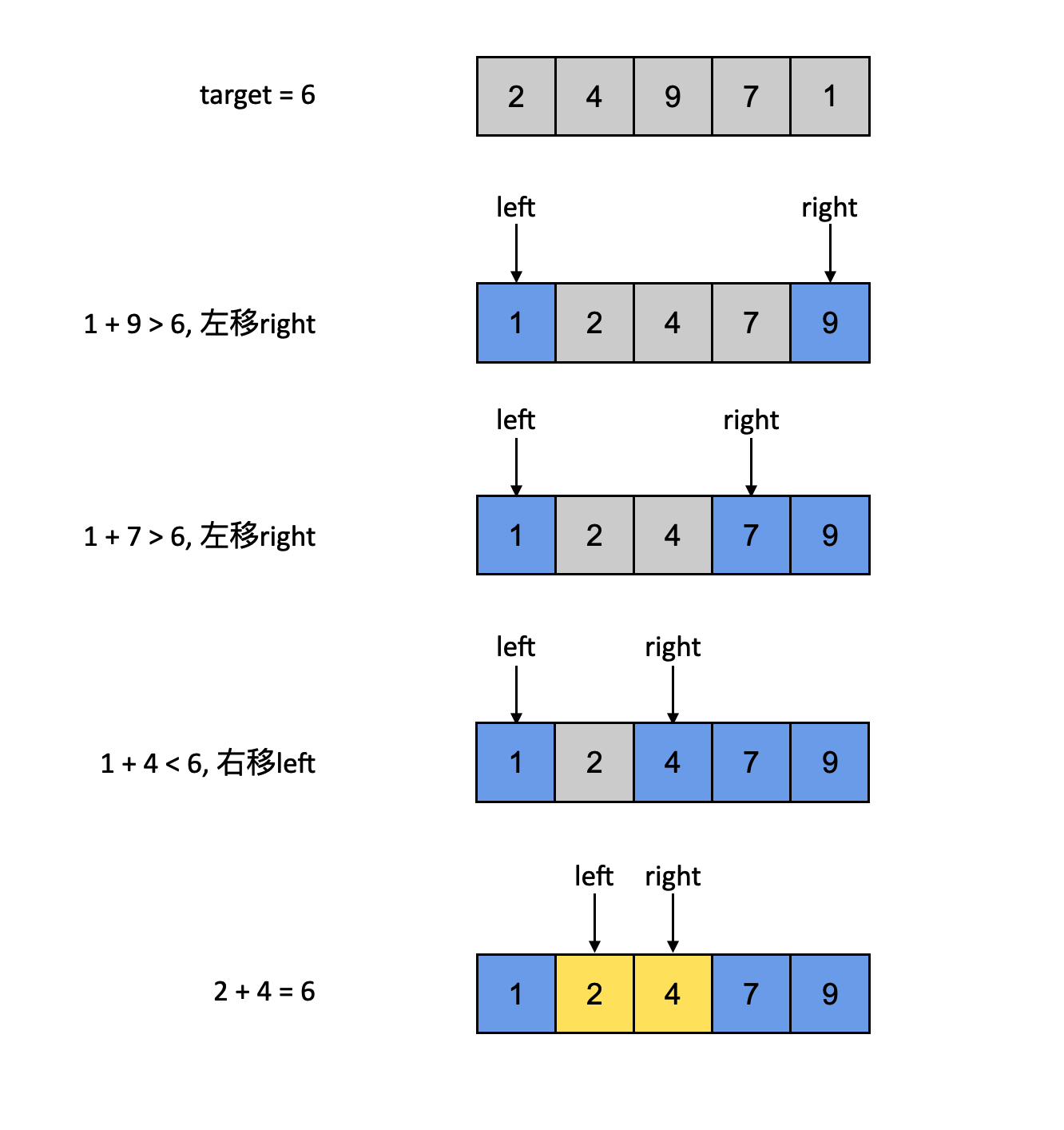
- 先将原数组进行排序(这里可以使用编程语言自带的排序方法)
- 创建left、right两根指针。left指向第一位,right指向最后一位
- 只要left和right不重合,循环比较left、right指向的两个数字的和sum:
- 如果sum等于target,那么left、right所指向的数字就是我们要找的结果
- 如果sum大于target,那么将right向左移动一位,让下一个sum变小
- 如果sum小于target,那么将left向右移动一位,让下一个sum变大
- 当循环结束,依旧没有答案,说明没有正确解
public int[] twoSum(int[] nums, int target) {
Arrays.sort(nums); // O(NlogN)
int left = 0;
int right = nums.length - 1;
while (left < right) { // O(N)
int sum = nums[left] + nums[right];
if (sum == target) {
// 如果sum等于target,那么left、right所指向的数字就是我们要找的结果
return new int[] {nums[left], nums[right]};
} else if (sum < target) {
// 如果sum小于target,那么将left向右移动一位,让下一个sum变大
left++;
} else if (sum > target) {
// 如果sum大于target,那么将right向左移动一位,让下一个sum变小
right--;
}
}
return new int[0];
}
这个算法的优势在于每次只会让较大的值减小、或者较小的值增大,得到的sum是连续的。如果存在正确的解,就一定可以找到对应的left和right。left、right的单调移动,每次会排除一部分错误答案,减小搜索空间,而且保证了数组中每个数字仅被访问一次,消耗是O(N)的。但是在预处理的时候使用了排序,所以会有O(NlogN)的时间消耗。总体上消耗了O(NlogN)的时间和O(1)的空间。缺点是改变了原数组的元素位置。
时间-空间的取舍
让我们来回顾这三种解法:
- 解法1消耗了O(N2)的时间和O(1)的空间
- 解法2消耗了O(N)的时间和O(N)的空间
- 解法3消耗了O(NlogN)的时间和O(1)的空间
与解法1的暴力算法相比,解法2是用了空间换时间,增加了Set的消耗,减短了查询的消耗。解法3则相反,用了时间换空间,通过原地排序,省去了Set。这两类操作统称space-time trade-off 空间-时间权衡。
通过对算法的复杂度分析,我们有了量化算法效率的方法。我们可以明确地指出,解法2比解法1更好,解法3比解法2消耗更少的内存。
| 数据结构 | 关键信息 |
|---|---|
| array | 通过下标访问O(1),查询O(N),插入O(N),删除O(N) |
| string | 在内存中的形式与array等价 |
| linked list | 通过下标访问O(N),查询O(N),插入O(1),删除O(1) |
| stack | last-in first-out,在内存中的形式等价于linked list |
| queue | first-in first-out,在内存中的形式等价于linked list |
| heap | 查询极值O(1),插入O(logN),删除极值O(N) |
| hash table | 插入、删除、查询O(1) |
| binary search tree | 插入、删除、查询、找最大最小值、访问前驱结点、访问后继节点均为O(1) |
大多数情况下,算法的过程是基于对基础数据结构的操作。因此分析算法复杂度也要求我们掌握常见的数据结构。上表给出了常用数据结构和操作的时间复杂度。记住这张表,能帮助我们更快的分析一个新算法的复杂度。
欢迎关注「慕课网」帐号,我们会一直坚持内容原创,提供IT圈优质内容,分享干货知识,大家一起共同成长吧!
本文原创发布于慕课网 ,转载请注明出处,谢谢合作