导读

意义：电子技术的进步使通道更多的时域功能近红外光谱(TD-fNIRS)得到发展。由于高阶时域矩的深度选择性，时域矩量分析已被提出用于提高对大脑的敏感度分析。研究者提出了一种综合时域(TD)矩量数据和辅助生理测量(如短分离通道)的一般线性模型(GLM)，以提高HRF的利用率。

目的：本研究比较了前人研究的多距离TD矩技术与常用的连续波(CW)fNIRS血流动力学响应函数(HRF)恢复技术(即block平均和CW GLM)的性能。此外，还比较了多距离TD矩技术和TD矩GLM技术。

方法：本研究用已知的合成HRFs增强了静息TD-fNIRS矩数据(6名被试)。然后，使用block平均和GLM技术，以及为CW和TD设计的“短分离回归”来恢复HRF。计算了均方根误差(RMSE)以及恢复的HRF与地面真值的相关性。用配对t检验比较了等效CW和TD技术的性能。

结果：研究者发现，相对于CW GLM，TD矩HRF恢复使HbO和HbR的相关性分别提高了98%和48%。与TD矩相比，TD GLM的相关性提高了12%(HbO)和27%(HbR)。相对于CW GLM，TD矩的RMSE分别降低了56%和52%(HbO和HbR)。发现与TD矩相比，TD GLM的RMSE没有统计学上的显著改善。

结论：适当的协方差尺度TD矩技术在HRFs恢复的RMSE和相关性方面都优于CW等效技术。此外，研究者提出的基于矩量的TD GLM优于常规的TD矩分析，同时允许纳入来自头皮的混合生理信号的辅助测量。

引言

功能近红外光谱(fNIRS)是一种测量大脑血流动力学功能变化的技术。连续波fNIRS (CW fNIRS)是fNIRS最常见的模式，其中光连续发射和探测。虽然这种设备易使用，但它的缺点是，难以区分伪影。

多年来，为了提高fNIRS中大脑信号的对比度，人们已经提出并实施了几种解决方案。最简单的方法是让被试在随机间隔内接受多次重复的任务或刺激，然后在刺激前后执行平均时间间隔。另一种更复杂的方法是一般线性模型(GLM)，它涉及到将测量信号用最小二乘拟合到一个线性模型中，该线性模型以辅助信号的形式包含额外信号[例如，用于模拟系统生理的短分离(SS)通道]。然而，CW fNIRS对大脑各层的低敏感性，以及信号的统计特性违反了GLM的假设，仍会使神经信号的解释复杂化。

时域fNIRS(TD fNIRS)是CW fNIRS的替代方案，它提高了对脑血流动力学的敏感性。TD fNIRS利用时间门控来区分到达探测器的光子作为它们传播时间的函数。由于光子传播距离较长，更有可能到达组织的深层，因此当选择传播距离较长的光子时，TD-fNIRS对脑血流动力学的敏感性有所提高。然而，这种相对于连续波fNIRS的优势在实际情况中受到仪器响应函数(IRF)的限制，这导致了传播时间分布(DTOF)的扩大，使时间门的解释复杂化。DTOF的矩量分析(相对不受IRF影响)已被提出作为TD-fNIRS中时间门分析的替代方法。与信号强度变化相比，较高的DTOF统计矩增加了对更深组织层的敏感性，因为矩量计算的内核作为传播时间的函数而增长。然而，文献中报道的TD矩分析仍然依赖于block平均来恢复血流动力学响应函数(HRF)，与GLM不同，它不允许混入HRF形状以外的信号。

本研究比较了矩量TD fNIRS与仅使用等效CW技术从静息时间序列数据中恢复HRF的性能。研究者还提出了一个GLM公式，对矩量数据进行线性回归，从而允许我们通过纳入辅助测量(如SS通道)来更好地区分HRF与头皮中的混杂生理干扰。通过比较得到的均方根误差(RMSE)和恢复的HRF的相关性来评估这些方法的性能。本研究表明，通过对TD矩量数据进行适当的协方差加权，可以获得最优的HRF估计。同时发现，最优方差加权不是传统上描述的泊松噪声相关的矩协方差。

理论

n＞0时，DTOF的n阶矩由：

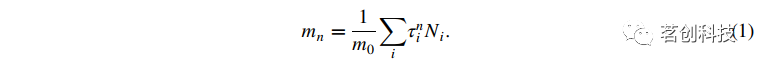
Ni是DTOF的第i个bin的高度(即，该bin中的光子数量)，τi的传播时间和第i个bin有关，m0为DTOF的第零阶，由∑iNi得到。在本研究中，定义M0=-log(m0)，给定时间样本的DTOF曲线下面积的对数，M1=m1，平均传播时间，和M2=m2-m12，DTOF的方差。本研究将M0，M1和M2称为“矩”。

根据Liebert等人的研究，如果j层样本的吸收系数有一个很小的变化，矩的线性变化为：

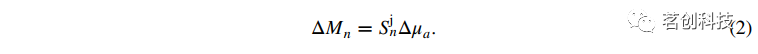
是Mn对j层吸收系数变化的灵敏度，是与测量通道相关的源-探测器分离ρ的函数。这些灵敏度可以通过蒙特卡罗(MC)模拟来估计。

公式(2)可以用来模拟fNIRS通道由于不同层吸收变化而引起的总矩变化。由Liebert等人提出，作为从多距离TD-fNIRS测量中恢复双层组织模型(大脑和头皮)吸收系数的诱发神经变化的一种方法，其表达式如下：

△

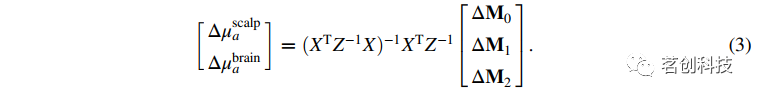
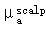
和△分别是表层和脑层吸收系数的变化。△Mn是包含从1到Ns的源-探测器分离矩变化ρi的列向量，其中Ns是具有不同距离的通道数。X是一个包含不同矩、距离和层数的灵敏度的矩阵，大小为3Ns×2(矩数乘以具有不同距离的通道数，再乘以层数)。Z是一个大小为3Ns×3Ns的协方差矩阵，包含与每个距离和矩相关的测量协方差。这些协方差可以从DTOFs中进行估计，假设信号中的方差是由泊松噪声主导，以及其他假设。公式(3)的所有元素都是波长相关的。

材料与方法

数据采集

使用Kernel flow TD-fNIRS系统获得了6名被试5分钟长的静息时间序列。被试在采集过程中看着一个空白的电脑屏幕。Kernel flow是一个TD-fNIRS系统，几乎完全覆盖整个头部。每个模块包含一个源和六个探测器，整个蒙太奇由52个源(双波长690和850nm)和312个探测器组成，共2206个通道，源-探测器分离范围在9.7到60mm之间，以7Hz采样。其中，312个短分离(SS)通道(＜10mm)，197个中分离(MS)通道(21~27mm)，317个长分离(LS)通道(28~34mm)，1380个超长分离(VLS)通道(＞34mm)。然而，由于存在某些实验问题(如头发染色、头发密度以及与头部的耦合不良)，因而并不是所有的通道都可用。平均而言，一个被试只有5.6%的VLS通道是可用的，而SS通道可用比例为73.9%。图1为头部通道位置的2D图(为清晰起见，不包括间隔大于34mm的通道)；根据不同被试在该区域可用的通道数量对这些通道进行颜色编码。

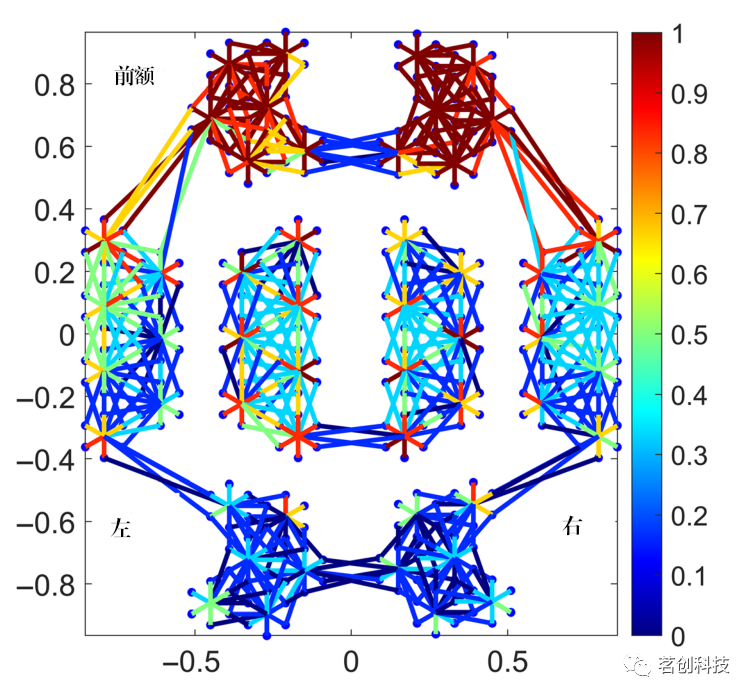
图1.头部通道的相对位置示意图。

利用合成HRF增强数据

研究者用随机间隔的合成HRF增强了静息时间序列的通道矩。这是通过使用Beer-Lambert定律将图2中的HRF转换为吸收系数的变化来完成的，然后使用公式(2)确定适当的源-探测器距离来确定矩的变化，以添加到静息矩时间序列(减去均值)。灵敏度

(ρ)由MC模拟计算，假设表层厚度为13mm。添加的HRF随机间隔，均值为21s，标准差为3s。通过这种方式，每个通道都增加了14次重复HRF。HbO的HRF振幅约为0.6μM，HbR的HRF振幅为−0.2μM。源-探测器间隔＜34 mm的通道被增强。由于较长的通道大多数都没有提供可用的信号，因而本研究排除了对这些通道的分析，这与其他典型fNIRS设备中的信号水平是一致的。

图2.合成HRF用于增强时间序列(标度1)。

此外，研究者还为HRF准备了其他振幅的附加增强数据。只需将图2中的HRF按0.2、0.5和3缩放即可获得备选的HRFs。这样做是为了研究信噪比(SNR)对HRF恢复技术的影响。图3比较了一个被试的通道(850nm)在三个时刻的原始静息时间序列与标度为3(同一通道)的增强时间序列。

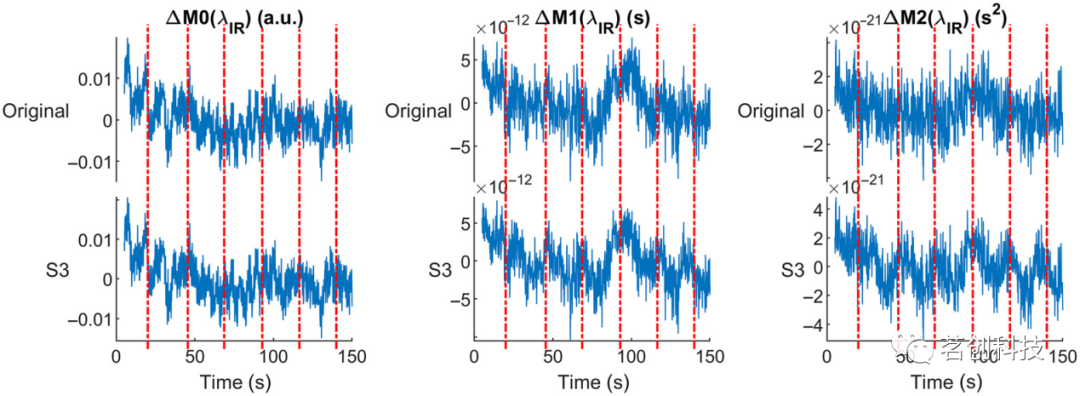
图3.850nm处原始静息时间序列与增强静息时间序列(标度3)的比较。值得注意的是，增加的HRF并不明显，时间序列的变化只有在高阶矩时才变得明显，因为后者对脑层吸收系数的变化更敏感。

蒙特卡罗模拟

研究者对多层介质中从源到探测器的光子进行了MC模拟，以计算公式(2)的灵敏度矩阵以及公式(3)中以泊松噪声为主导的协方差矩阵。这些模拟是用蒙特卡罗极限(Monte Carlo eXtreme)进行的。模拟用于计算头皮层厚度、源-探测器分离，以及基础吸收系数变化的敏感性查阅表。在增强静息数据和恢复HRF期间，可以快速调用这些查阅表。

对于特定的吸收系数和源-探测器分离的20层中的每一层的灵敏度值，可以用线性插值从这个表中最近的值计算出来。表层的灵敏度是通过对第一个Tscalp层的灵敏度求和来计算的，其中Tscalp是表层的厚度，单位为mm；类似地，大脑层的灵敏度是通过将Tscalp+1及以上层的灵敏度相加来计算的。

通过首先计算基础组织的DTOFs，然后计算DTOFs的四阶矩，还从MC模拟中计算了泊松噪声主导的协方差。然后通过线性插值得到特定源-探测器分离和吸收系数的矩，并将其输入公式(12)到(17)计算出方差。并称这个理论上的协方差矩阵为ZT。

用分段平均法从TD矩中恢复HRF

使用Liebert等人描述的多距离矩方法从增强的静息数据中恢复HRF。研究者将这种技术称为TD矩。对于系统中的312个探测器，分别选择1个LS通道和1个SS通道。每个探测器的LS通道被选为可用(高质量信号)通道，源-探测器距离最接近30mm(且＜34 mm)。实际上，所有具有可用的LS通道的探测器也具有可用的SS通道(所有被试中只有1%没有)。只有可用SS通道的探测器被排除在大多数分析之外。仪器对于低质量信号的通道会呈现非数字，所以这些低质量通道不能使用。所有可用的通道都被认为是“优质”的。

使用TD矩技术[公式(3)]仅使用LS通道或LS+SS通道(因为该技术允许多距离)恢复HRFs。研究者将这两种方法分别称为TD LS和TD LS+SS方法。TD矩技术使用公式(3)测量到的矩的变化来估计大脑和头皮层的吸收变化。在估计了大脑的吸收变化后，根据模拟刺激时间对这些吸收变化进行了block平均。然后将block平均值转换为血红蛋白浓度的变化，并与实际情况进行比较。

为了正确求解公式(3)，需要估计协方差矩阵Z。研究者尝试了两种估计协方差的方法。第一个是利用Liebert等人的方程进行MC模拟，计算理论上的泊松噪声主导的协方差ZT。第二种方法是直接从测量的时间序列中计算矩的协方差。首先定义矩量矩阵：

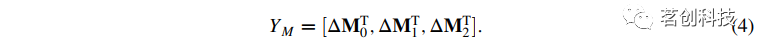
△Mn为Nc×Nt向量(Nc为用于多距离分析的通道数，Nt为采样的时间点数)。YM大小为3Nc×Nt；上标T表示矩阵转置。在使用两个距离的情况下，即同时使用LS和SS通道，ΔMn的两行中有一行是LS通道的测量值，另一行是SS通道的测量值。(注：如果进行单距离分析，则ΔMn为1×Nt)可以计算协方差矩阵的估计值为：

ZE为根据数据估计出的协方差矩阵，大小为3Nc×3Nc。

使用ZT和ZE从公式(3)中计算层分离，以比较每种协方差缩放方法的性能。除非另有说明，本文中所示的TD技术的大多数结果都使用了从数据ZE估计的协方差。

在计算公式(3)时使用缩放，以改善矩阵被反转的条件数，从而防止数值不稳定。为此，估计量X*计算为：

它在代数上等价于公式(3)中X*=(XTZ−1X)-1XTZ-1给出的标准加权最小二乘表达式。这里k是一个对角矩阵，用于对每个矩量施加权重，使其单位具有相似的刻度。

此外，研究者用TD矩技术恢复了HRF，每个探测器只使用一个SS通道。并将其称为TD SS。这样做是为了评估TD SS与TD LS的比较，因为过去的一些研究表明，在TD-fNIRS中，SS通道中可用光子数量比LS通道高得多，可以弥补SS通道中大脑灵敏度的损失。

为了进行比较，使用改进的Beer-Lambert定律将ΔM0(相当于CW光密度测量值)转换为血红蛋白浓度的变化，然后对增强数据进行常规CW block平均(在0.7Hz截止频率低通滤波后)，然后再进行block平均。还将常规CW GLM技术应用于增强数据，使用LS和SS回归比较CW。设计矩阵采用间距和标准差均为1s的高斯基，并按照Gagnon中描述的方法加上SS通道。没有使用多项式漂移项，也没有对SS通道应用延迟。

研究者计算了每个探测器恢复的HRF与真实情况之间的RMSE和Pearson相关性，以比较不同恢复技术的性能。通过减去-2~0s的HRF均值来对恢复的HRF进行基线校正。Pearson相关系数经过 Fisher变换，转化为正态分布。Fisher变换由以下表达式给出：

其中r为Pearson相关系数，z为Fisher变换Pearson相关系数。接下来，所有已知的相关性都会进行Fisher变换。使用配对t检验(α=0.05)比较处理组之间的RMSE和相关性。

TD矩的GLM

除了使用TD矩技术处理增强数据外，研究者还提出、实现并演示了一个GLM来分析TD fNIRS矩，该GLM还同时对头皮中的混杂生理信号进行了建模。TD GLM基于以下假设：在给定通道中观测到的第n阶矩的变化是由大脑血流动力学变化引起的矩变化与生理、其他伪影引起的矩变化的线性叠加，而后者主要在头皮观察到，即：

这里Δ

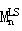
是测量到的LS通道第n个矩的变化，作为波长λ的时间函数。Δ(λ，t)是头皮/表层对矩变化的贡献，Δ(λ，t)是大脑层的贡献。βSS(λ)是一个耦合常数。由公式(2)可知，公式(8)第一项从头皮层开始的矩变化可表示为：

其中，

(λ，ρLS)为LS通道对头皮吸收系数变化的敏感性，Δμscalp(λ，t)为头皮层吸收系数变化。假设有一个SS测量的变化在第零时刻Δ(λ，t)。由于与头皮层相比，第0阶矩对大脑层的敏感度较低，可以使用公式(2)进行近似:

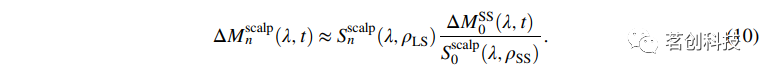
这里的

(λ，ρSS)是对头皮层SS通道第0阶矩的吸收系数变化的敏感性。同理，公式(8)的第二项可以表示为：

其中脑层吸收系数的变化用Beer-Lambert定律表示为血红蛋白浓度的变化。

(λ，ρLS)是对脑层LS通道第n阶矩的吸收系数变化的敏感性。ϵHbX(λ)为血红蛋白种类对应的消光系数，而Δ(t)是它们在大脑层的浓度变化。现在，将血红蛋白浓度的变化表示为Nβ时间基函数gk(t)的线性组合：

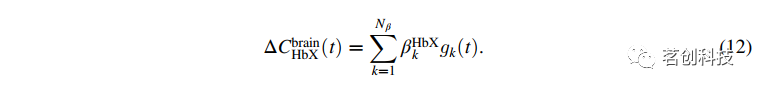
结合公式(8)、(11)和(12)：

公式(13)为LS通道的线性模型，为时域基函数和由公式(10)建模的头皮所引起的矩变化之和。如果有一系列矩变化的时间测量值，可以用矩阵形式表示为：

这里Δ

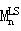
是LS通道观测到的第n阶矩变化的测量值的列向量，其大小为2Nt×1(Nt为时间样本的数量)。β是包含回归系数的列向量，其长度为2Nβ+2。Un为矩n[大小为2Nt×(2Nβ+2)]的设计矩阵。β为：

矩n的设计矩阵为：

Δ

(t)为：

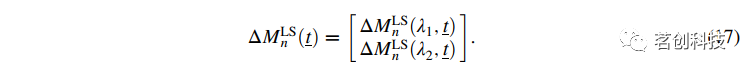
Δ

(λ，t)为波长λ的LS通道中矩n的测量变化量。定义缩放基函数(t，λ)为：

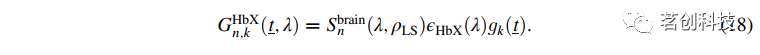
现在，如果测量0到2的矩的变化，可以根据公式(14)将所有测量值合并到一个矩阵中：

接下来，定义：

和

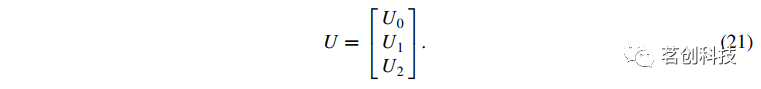
然后可以求解公式(19)中的回归系数β：

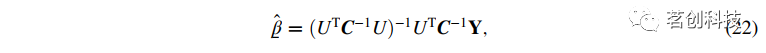
其中C是测量值的协方差矩阵。C的大小为6Nt×6Nt，在泊松噪声主的情况下，可以通过理论计算得到。或者，假设通道中没有序列相关性(白噪声)，可以从测量数据中进行估计：

其中⊗代表Kronecker积，I(Nt)是Nt阶的单位矩阵。cov(YM,YM)为矩阵YM的协方差矩阵。YM定义为：

YM的大小为Nt×6[与公式(4)中的YM类似]。事实上，C矩阵是与适当的单位矩阵进行Kronecker积后的Z矩阵。

结果

图4显示了通过TD(LS+SS)矩分析从大脑层(上)和表层(下)获得的block平均HbO(红色)和HbR(蓝色)的示例。这是一个被试前额叶皮层的一个通道。HbO用红色曲线表示，HbR用蓝色曲线表示。上图还用橙色和紫色(分别为HbO和HbR)显示了HRF的真值。

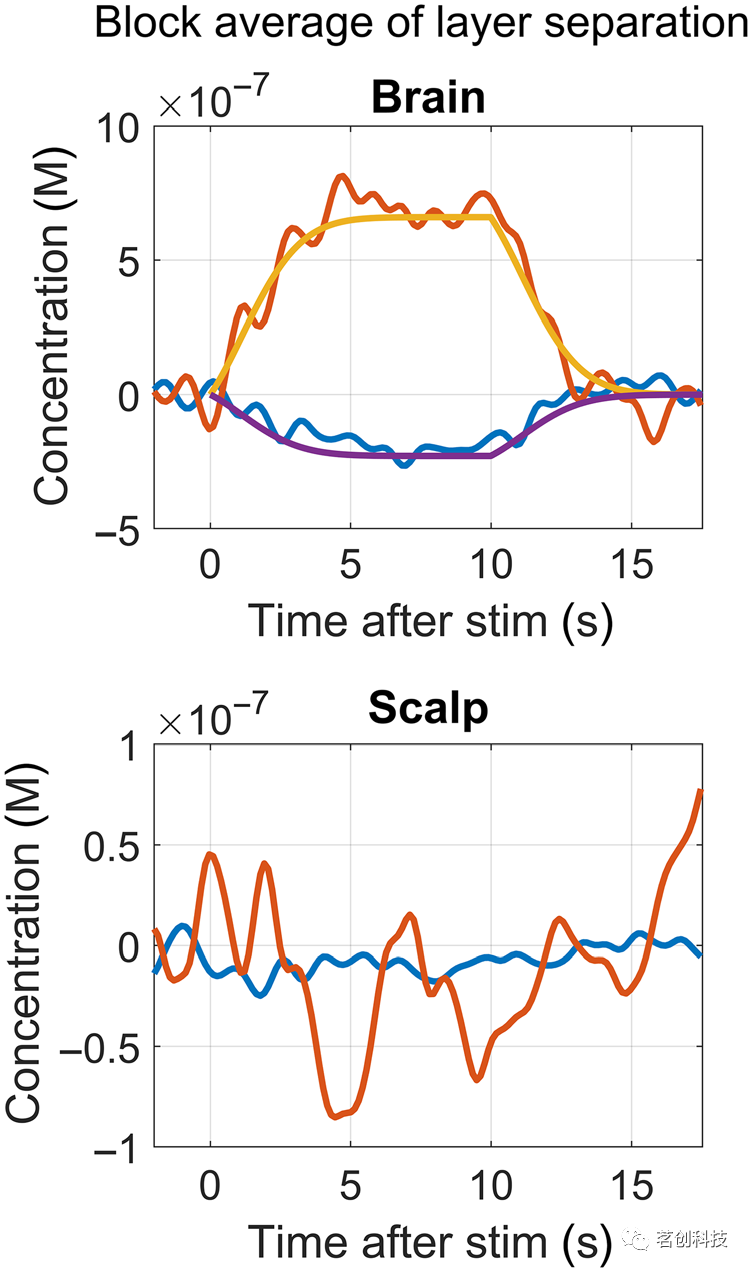
图4.以一个通道的HbO(红色)和HbR(蓝色)block平均为例，应用多距离TD矩分析来分离大脑和头皮。上图还显示了HRF真值(橙色代表HbO，紫色代表HbR)。

图5显示了本研究使用的几种技术恢复HRF的示例；这里GT为真值，TD为TD(LS+SS)矩技术，GLM CW是仅从CW(M0)数据计算出的GLM, GLM TD为时域矩GLM。每种技术显示的HRF是其中一个通道(通道14)的各被试平均值。

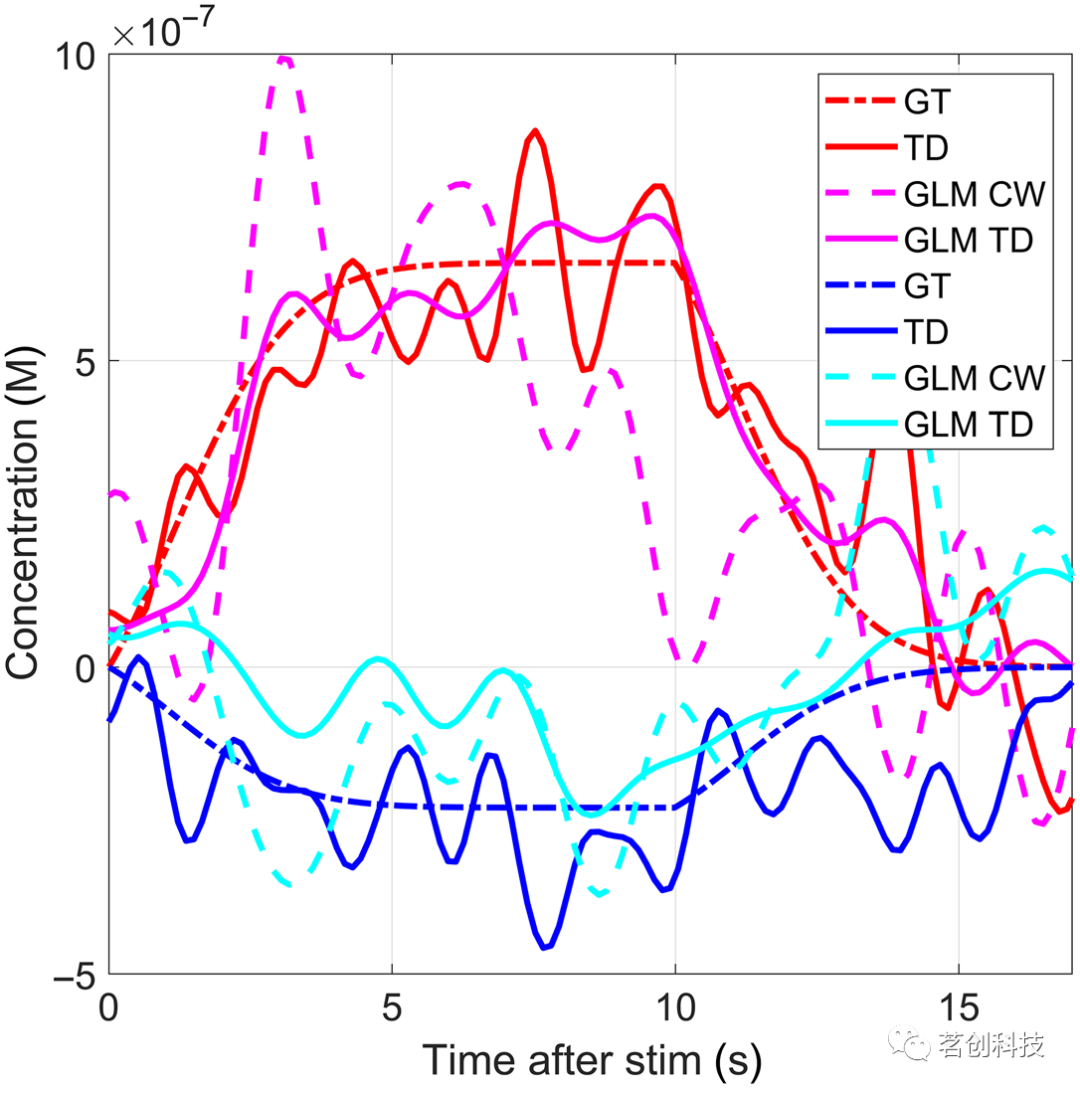
图5.使用不同技术获得的恢复HRFs及其真值。

图6显示了比较所有被试和通道(包括HbO和HbR)从恢复的HRF中获得的RMSE和Fisher转换相关性的箱线图。TD LS+SS是多距离TD矩分析，CW GLM是传统的带SS回归的CW GLM。TD LS是一种只有一个距离(LS)的矩分析技术。还包括TD SS(单距离矩分析技术，SS)和CW SS(SS通道CW波数据的block平均)。TD技术在所有发色团和指标上都优于CW技术(α=0.05)。本研究发现TD LS+SS与TD LS(α=0.05)的HbR相关性和HbO RMSE差异不存在统计学显著性，说明添加SS信息，总体上没有显著提高LS在时域上的性能。

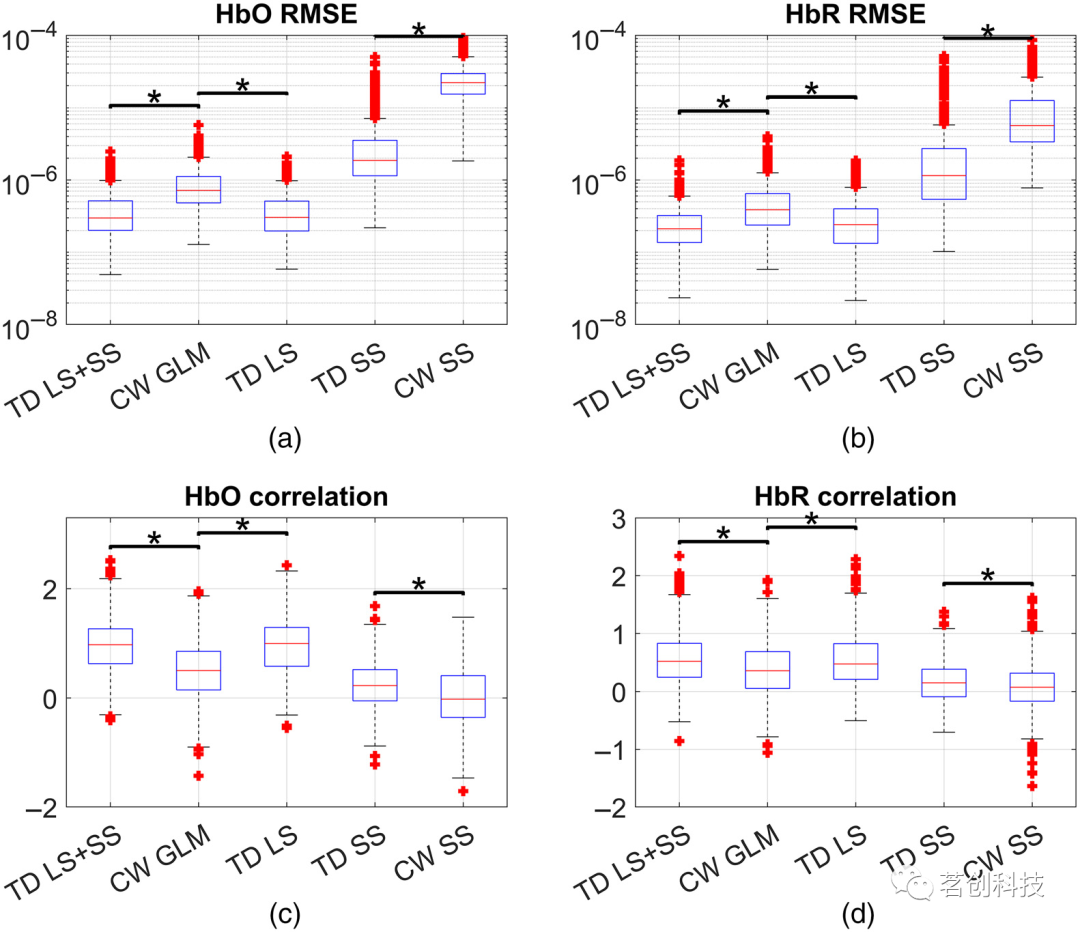
图6.所有被试和通道(包括HbO和HbR)的RMSE和Fisher转换相关性的箱线图。

图7比较了TD GLM与TD矩分析的性能，同时纳入了CW GLM进行比较。所显示的结果包括所有被试和通道。TD GLM在相关性上优于TD矩分析，但在RMSE方面则不是。平均而言，TD矩HRF恢复使HbO和HbR的Fisher转换相关性比CW GLM分别提高98%和48%。TD GLM的Fisher转换相关性比TD矩提高了12%(HbO)和27%(HbR)。相对于CW GLM，TD矩的RMSE分别降低了56%和52% (HbO和HbR)。

图7.对HbO和HbR(在所有被试和通道上)的GLM性能(CW和TD)进行简单的双距离矩分析。

图8用于举例说明协方差缩放选择对所有被试和通道的HbO RMSE的影响。该图左侧的三个框是block平均技术，其中CW LS是LS通道的CW block平均，TD LS ZT是使用理论泊松噪声主导的协方差(ZT)对LS通道进行TD矩分析，TD LS ZE是使用从数据估计的协方差(ZE)进行TD矩分析。同样，右边的三个框是GLM技术，从简单的CW GLM开始，然后用理论的泊松噪声主导的协方差缩放ZT TD GLM，TD GLM ZE是使用从噪声估计的协方差进行缩放的TD GLM。

图8.协方差缩放对所有被试和通道的HbO RMSE的影响。

图9显示了TD技术的HRF振幅如何影响HbO与真值的相关性，并将CW GLM作为对比。它显示了添加HRF的相对振幅如何影响不同技术的性能，通过Fisher转换相关来测量。

图9.比较不同HRF标度下HbO在所有被试和探测器上的平均Fisher转换相关性。

讨论

连续波技术和矩技术

虽然替代的fNIRS采集技术，如TD fNIRS和FD(频域)fNIRS，比传统的CW fNIRS提供了许多理论上的优势，但一些实际情况阻碍了其使用。特别是，TD和FD fNIRS需要更复杂和精确(也可能更昂贵)的仪器，以及更复杂的处理技术，才能充分发挥其潜力。由于这些原因，与CW fNIRS相比，FD和TD的商用设备数量非常有限。同时在市面上，相对于仅提供有限通道数量的FD系统和TD系统，提供CW fNIRS系统的商家更多，而且后者的通道数量也在不断增加，使全头部覆盖和高密度开始成为常规。这导致TD和FD的研究经验相对缺乏，因此很难确定与CW fNIRS相比的优势是否能够完全实现。同样，IRF对TD fNIRS的影响会影响对来自不同组织层的光子的正确辨别。从这个意义上说，矩分析被提出作为TD fNIRS分析的一种替代方法，相对不受IRF的影响。本研究结果支持TD fNIRS时间序列的矩分析在恢复功能血流动力学神经反应方面优于等效的CW fNIRS技术，因为它增加了对更深组织层的敏感性。

TD GLM与多距离TD矩分析

TD GLM优于CW GLM和LS+SS的多距离矩分析。由于多距离分析比TD GLM更简单，计算成本更低，可能在某些情况下更适合使用简单的多距离TD矩分析。然而，由于硬件或实验的限制(即，并非所有通道都具有良好的信噪比)，并不总是可以进行多距离测量。事实上，传统的fNIRS系统只使用一个固定的源-探测器分离(30mm)，而可定制的距离和SS通道近年来才变得越来越流行。

多距离TD矩分析假设分析中使用的所有通道都在观察大脑层中吸收系数的相同变化，如果变化在空间上偏向其中一个通道而远离其他通道，则不一定是现实的(本研究分析假设与探测器相关的所有通道都在观察大脑层的同一区域)。GLM不需要这种假设，事实上，如果SS通道不包含来自HRF的贡献，GLM的效果会更好。这就是本研究的TD GLM模型只对SS使用M0的原因，因为高阶矩对大脑层的贡献更高，因此使用它们来建模表层会产生更差的结果。此外，研究者发现TD GLM在统计相关性上比TD LS+SS有显著的改善，但在RMSE方面没有明显改善。可以认为相关性是一个比RMSE更好的度量标准。RMSE的另一个缺点是高度依赖于从估计HRF中去除基线的方法。

TD GLM优于(多距离)TD矩分析的另一个论点是，TD GLM的性能可能比通过结合相关辅助信号的多模态回归得到的性能更高。选择不同的时域基也可能有利于某些情况，例如，在适当情况下使用标准的gamma函数，可以减少回归问题的自由度。此外，自回归技术可用于求解TD GLM。

与常规的CW GLM公式不同，本研究的TD GLM将两个波长的信息集成在一个模型中，避免了对氧合血红蛋白和脱氧血红蛋白进行单独计算的必要。此外，该模型执行从矩到浓度的转换，所需的预处理步骤更少。最后，对于有多个距离的重叠通道的情况，可能更好的方法是开发一种包含矩分析的图像重建技术，而不是使用多距离技术，因为图像重建技术可以更好地模拟血流动力学扰动的空间分布。

HRF振幅的影响

对多个HRF振幅的分析表明，即使在不同标度上，TD技术也优于CW技术。TD矩LS+SS优于CW GLM和TD GLM优于TD矩LS+SS的模式适用于所有用于HbO和HbR相关性的标度。RMSE也观察到类似的模式。对于较低幅值的HRF，CW GLM的性能相对较差，CW GLM和TD GLM之间的相关性差异随着幅值的增大而减小。

结论

本研究比较了TD-fNIRS矩技术与等效CW fNIRS技术在估计增强静息时间序列的HRF方面的性能。结果发现，只要使用适当的协方差缩放，并采取措施防止数值不稳定，TD矩技术在RMSE和与真值的相关性方面优于CW技术。此外，本研究提出了一种用于TD矩的GLM，通过纳入其他辅助测量的知识(例如来自头皮的混合生理信号的独立测量)，进一步提高了与基于非模型的LS+SS TD矩拟合相比的性能。

原文：How much do time-domain functional near-infrared spectroscopy (fNIRS) moments improve estimation of brain activity over traditional fNIRS？

DOI: 10.1117/1.NPh.10.1.013504