Problem - D - Codeforces

一个由整数p1,p2,...,pn组成的数组，如果它包含1到n中的每一个数字恰好一次，则称为一个排列组合。例如，下面的数组就是排列组合： [3,1,2], [1], [1,2,3,4,5] 和 [4,3,1,2]. 下列数组不是排列组合： [2],[1,1],[2,3,4].

有一个长度为n的隐藏的互换。

对于每个索引i，你会得到si，它等于所有pj的总和，使得j<i和pj<pi。换句话说，si是第i个元素之前小于第i个元素的元素之和。

你的任务是恢复这个排列组合。

输入
第一行包含一个整数n（1≤n≤2⋅105）--排列组合的大小。

第二行包含n个整数s1,s2,...,sn（0≤si≤n（n-1）2）。

保证数组s对应于长度为n的有效排列组合。

输出
打印n个整数p1,p2,...,pn--恢复后的排列组合的元素。我们可以证明，答案总是唯一的。

例子
输入复制
3
0 0 0
outputCopy
3 2 1
输入复制
2
0 1
输出拷贝
1 2
输入复制
5
0 1 1 1 10
输出拷贝
1 4 3 2 5
注意
在第一个例子中，对于每一个i，都没有满足两个条件的索引j，因此si总是0。

在第二个例子中，对于i=2，刚好j=1满足条件，所以s2=p1。

在第三个例子中，对于i=2,3,4只有j=1满足条件，所以s2=s3=s4=1。对于i=5，所有j=1,2,3,4都有可能，所以s5=p1+p2+p3+p4=10。

题解:
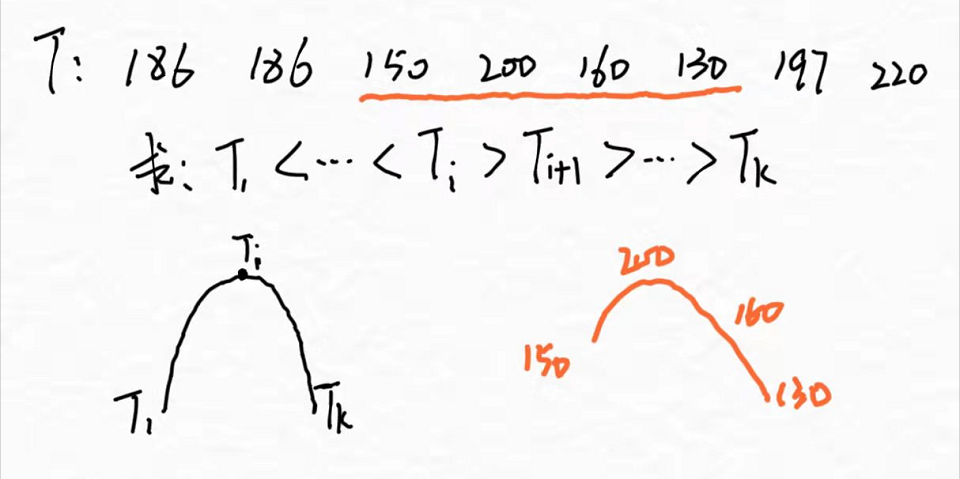
利用数组数组维护前缀和,每个位置记录该点的值,从最后面开始二分(这样后面的不会前面影响,到找前面时也不会被后面影响),如果没有找到,找到后再从删除这个值,继续往下找,

#include <cstdio>
#include <cstring>
#include <algorithm>
#include<iostream>
#include<vector>
#include<set>
#include<map>
#include<cmath>
#include<queue>
using namespace std;
typedef long long ll;
#define int long long
typedef pair<int,int> PII;
int n;
int a[200050];
int tre[200050];
int lowbit(int x)
{
	return x & -x;
}
void add(int s,int w)
{
	for(int i = s;i <= n;i += lowbit(i))
	tre[i] += w;
}
int sum(int s)
{
	int ss = 0;
	for(int i = s;i;i -= lowbit(i))
	{
		ss += tre[i];
	}
	return ss;
}
int ans[200050];
void solve()
{
	cin >> n;
	for(int i = 1;i <= n;i++)
	{
		cin >> a[i];
		add(i,i);
	}
	for(int i = n;i >= 1;i--)
	{
		int l = 1,r = n;
		while(l <= r)
		{
			int mid = (l + r)/2;
			if(sum(mid) <= a[i])
			{
				l = mid + 1;
			}
			else
			{
				r = mid - 1;
			}
		} 
		add(l,-(l));
		ans[i] = l;
	}
	for(int i = 1;i <= n;i++)
	cout << ans[i] <<" ";
}


signed main()
{
//	ios::sync_with_stdio(0);
//	cin.tie(0);cout.tie(0);
	int t = 1;
//	cin >> t;
	while(t--)
	{
		solve(); 
	}
}