来自Manolis Kellis教授的课

教了隐马尔可夫在基因组学中的一些应用

重点介绍了隐含状态序列解码问题

至于序列概率估计和求解参数问题没有细讲

本文浏览需要一定基础，需要的同学可以找b站看唐宇迪老师：隐马尔科夫
由于内容参考多个地方，其中符号表示存在差别，但是意义相同。比如Q、I都表示隐含序列

Modeling biological sequences with HMMS

这些术语涉及基因结构和基因表达：

1. Intergenic: 这指的是染色体上基因之间的DNA区域。
2. CpG Island: CpG岛是DNA区域，其中包含高密度的CpG位点（紧跟着胞嘧啶核苷酸的鸟嘌呤核苷酸区域）。这些区域通常位于基因启动子附近，并可以在基因调控中发挥作用。
3. Promoter: 启动子是位于基因上游的DNA区域，用作RNA聚合酶的结合位点，RNA聚合酶是转录基因的酶。
4. First Exon: 外显子是编码DNA区域，被转录成mRNA，并最终被翻译成蛋白质。基因中的外显子由内含子分隔开。第一个外显子是紧接着基因启动子区域之后的外显子。
5. Other Exon: 任何位于基因中第一个外显子之后的外显子。
6. Intron: 内含子是基因的非编码DNA区域，插入基因的编码序列（外显子）中。

1. 能够发射特定类型的DNA序列： 指一个生物体或样本具有发射某种特定类型的DNA序列的能力。这些DNA序列可能与之前已知的基因不完全相同，但仍保留了该类型的某些特征或性质。
2. 能够识别特定类型的DNA序列状态： 指在DNA序列中能够识别某种特定的状态，如一段序列是起始子、外显子、内含子等。通过机器学习算法，可以确定哪个隐藏的状态最有可能产生观察到的结果，并找到一组状态和转移关系，以生成较长的DNA序列。
3. 能够学习每个状态的特征： 指通过机器学习算法训练生成模型，以学习每个状态所具有的特征，以便在给定DNA序列中识别这些状态。通过在大型DNA序列数据集上训练生成模型，可以学习区分每个状态的特征，并且可以利用这些特征来对未标记的DNA序列进行分类。

Parsing longer sequences.

dependencies between netighoring positions

根据前面学过的生成模型，告诉我们，不仅要考虑隐藏层和观察层，还要考虑隐含状态间的转移关系

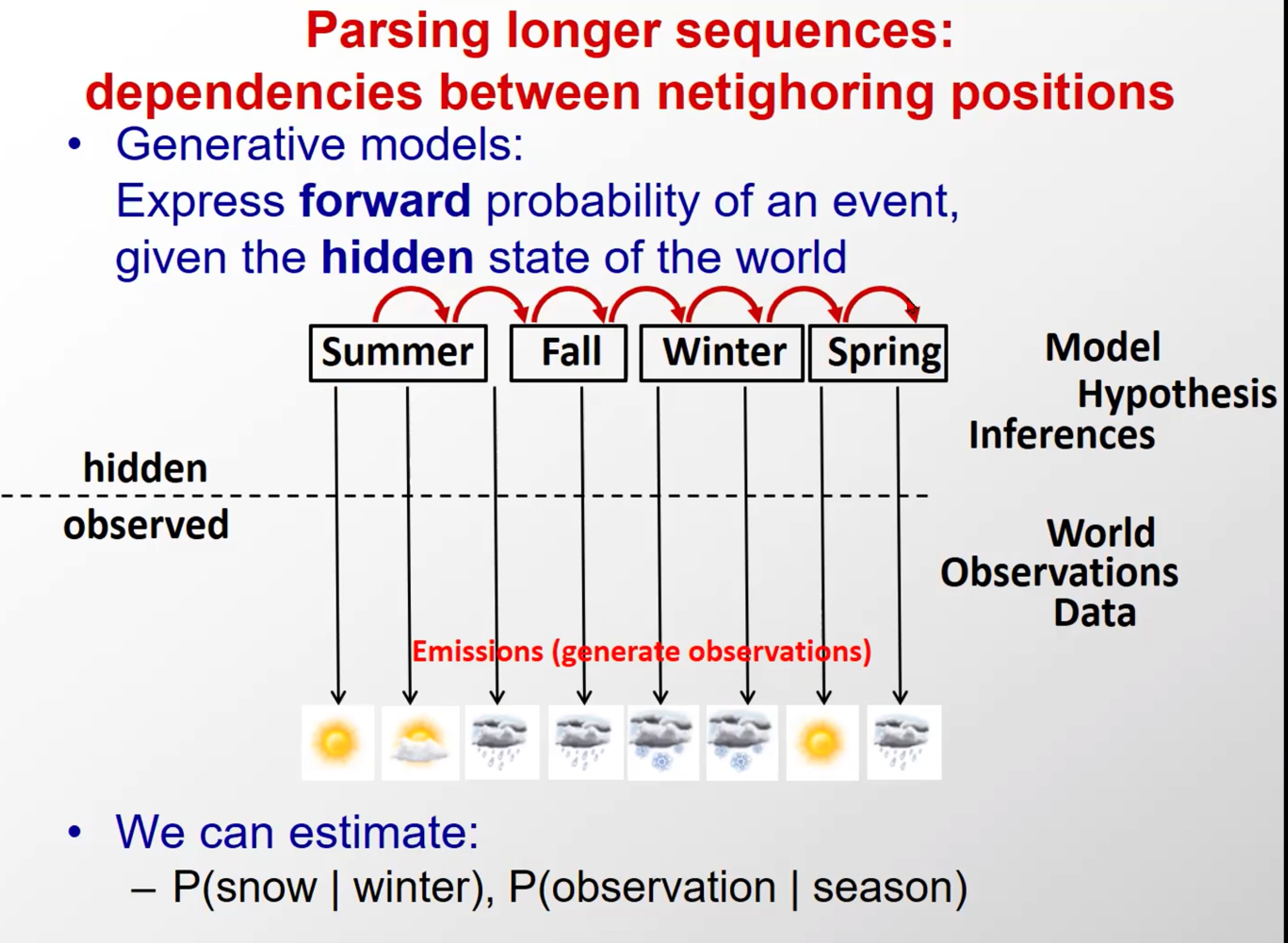
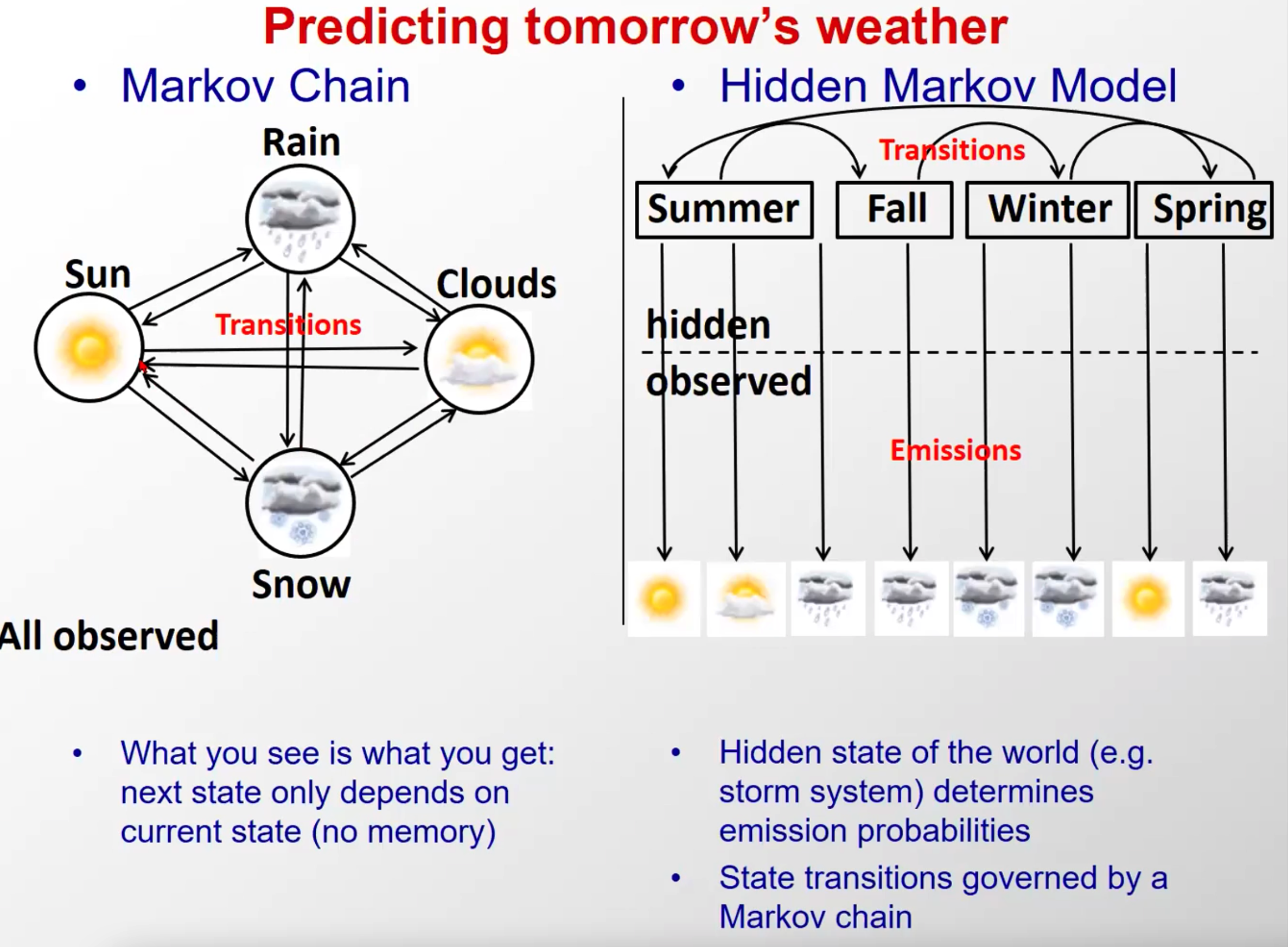
• 马尔科夫链和隐马尔科夫的概念

马尔科夫链其实很简单，网上视频很多

隐马尔科夫好的教程比较少，这是我认为不错的：隐马尔科夫

不懂的多网上搜搜就会了

这个图里，马尔科夫链的隐含态是天气，在隐马尔科夫中天气是观察态，季节是隐含态，注意区分

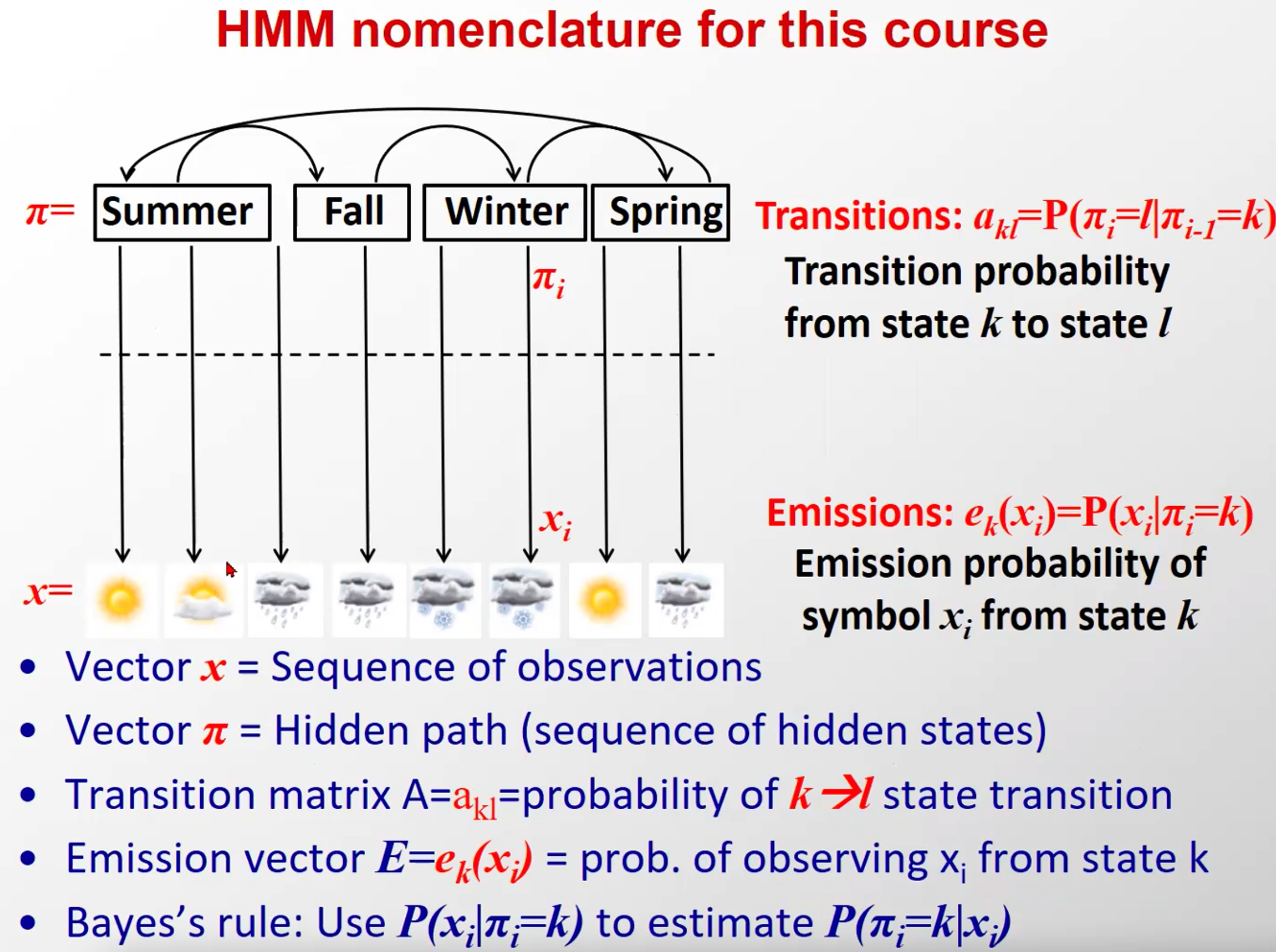
（符号表述有所不同）

三要素：上面这些都是隐马尔科夫模型的外在表征，而推动隐马尔科夫模型$\lambda$ 随着时间不断运行的内核是他的三要素：状态转移矩阵$A$，观测概率矩阵（也叫输出概率矩阵）$B$，以及初始隐含状态概率向量$\pi$，简写成三元组的形式就是：$\lambda =(A,B,\pi )$

主要研究问题：

1. 第一个研究的内容是观测序列概率估计： 当我们知道老千切换三个骰子的转移概率矩阵以及各个骰子输出各个点数的概率的基础上，我们可以计算出任意一个观测序列出现的概率，比如老千连续掷出诡异的8个6，我们可以看看这种情况发生的概率有多大。
   • 用隐马尔科夫模型的形式化语言概况就是：在给定隐马尔科夫模型三要素 $\lambda =(A,B,\pi )$的基础上，针对一个具体的观测序列$O=(o1,o2,...,oT)$，求他出现的概率。
2. 第二个研究的内容是隐含状态序列解码： 当我们知道老千切换三个骰子的转移概率以及各个骰子输出各个点数的概率时，我们可以通过已知的观测序列，也就是骰子的点数序列，来解码出老千所使用的骰子的序列，也就是隐状态序列。换句话说，就是可以推测出每一个掷出的点数背后，老千到底用的是哪一个骰子，可以判断他什么时候出千。
   • 用隐马尔科夫模型的形式化语言概况就是：在给定隐马尔可夫模型三要素$\lambda =(A,B,\pi )$和观测序列$O=(o1,o2,...,oT)$的基础上，求最有可能对应的隐藏状态序列 $I=(i_1,i_2,...i_T)$。

举例子

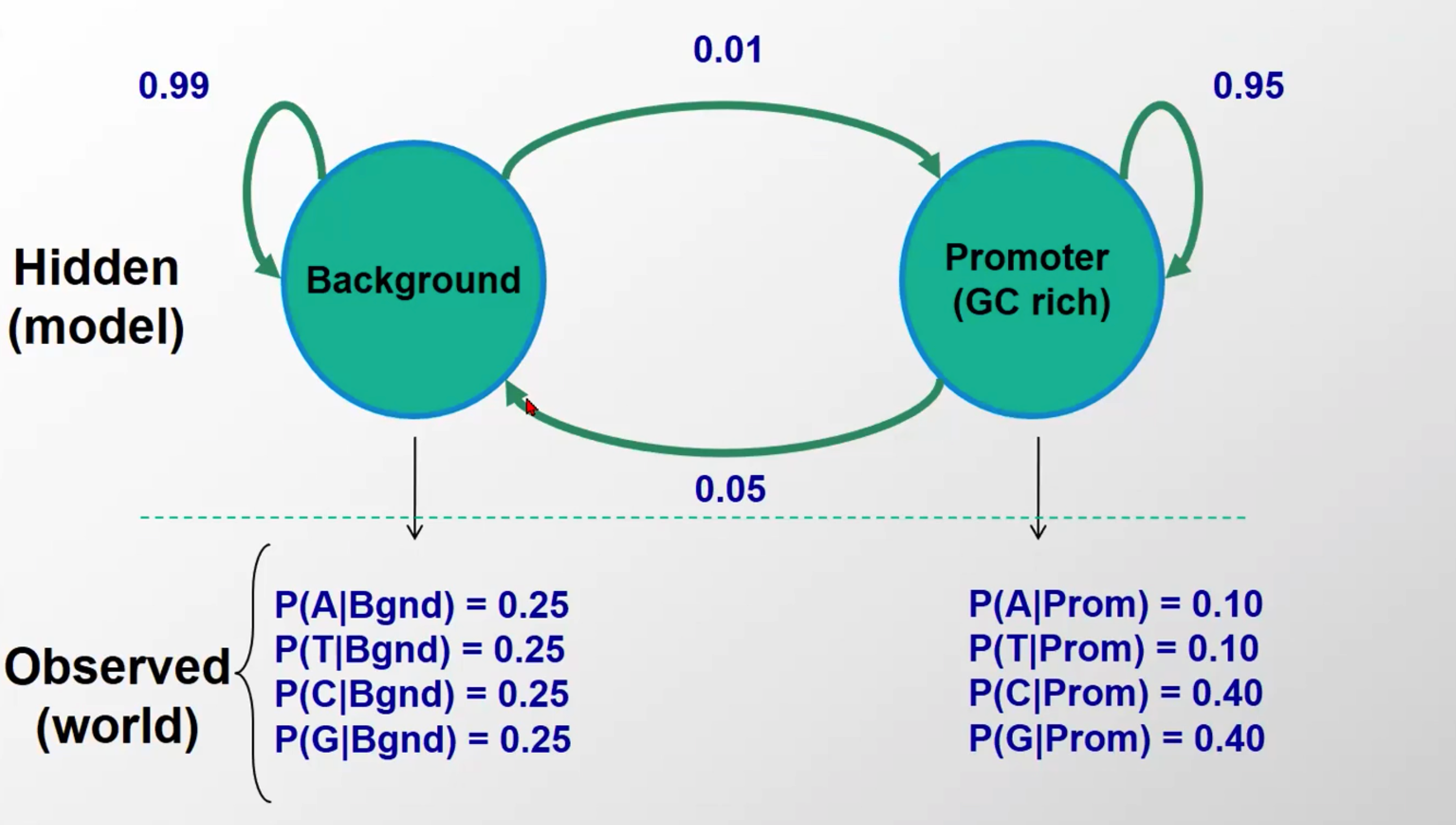
Our frst HMM: Detecting GC-rich regions

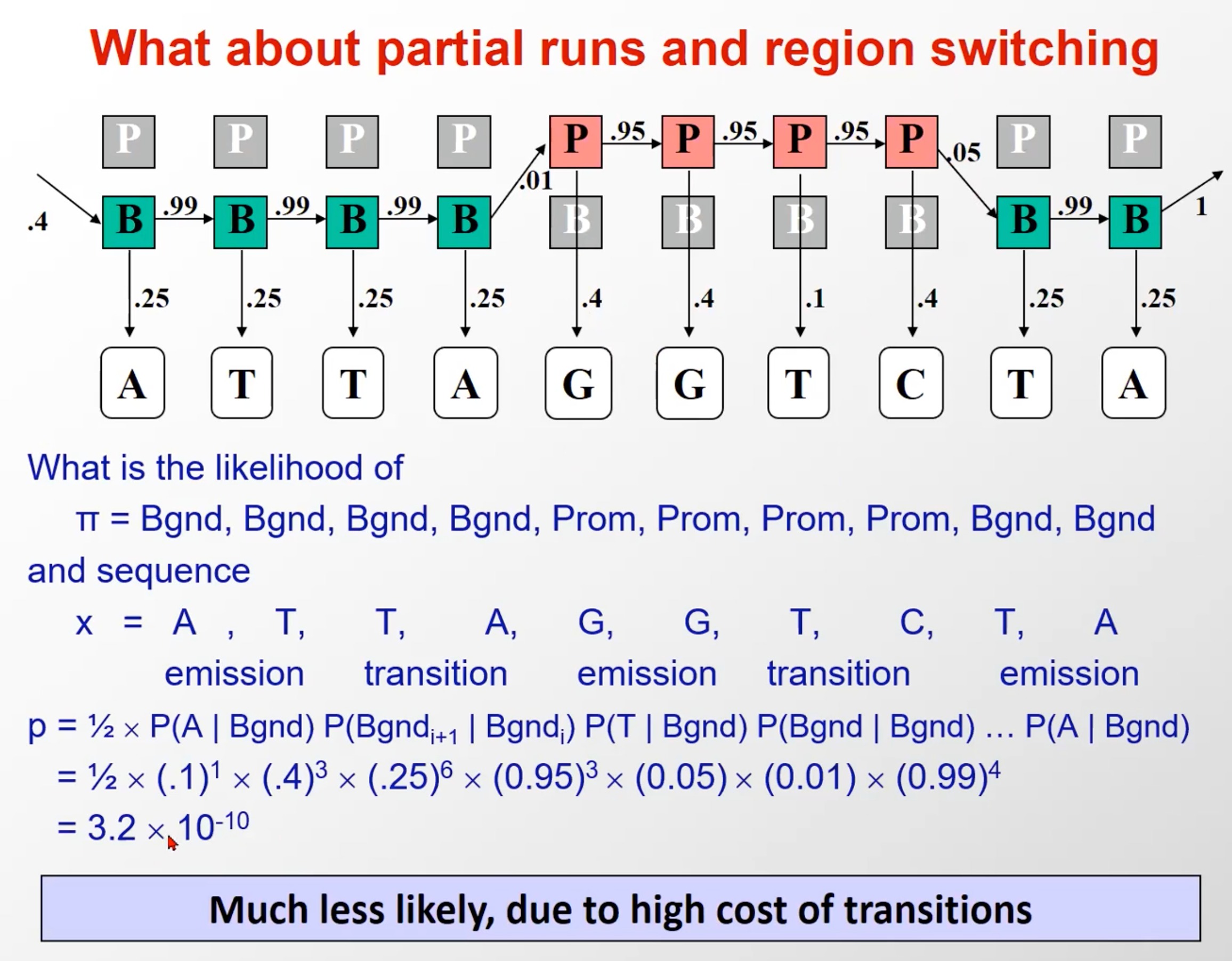
观察态：一般序列（background）里四种碱基出现概率一样，而启动子序列中GC出现的概率高一些

隐含态：前一个碱基是属于background的情况下，下一个碱基99%还是background，1%是启动子。而前一个碱基是属于启动子的情况下，其下一个碱基有95%是启动子，5%是background

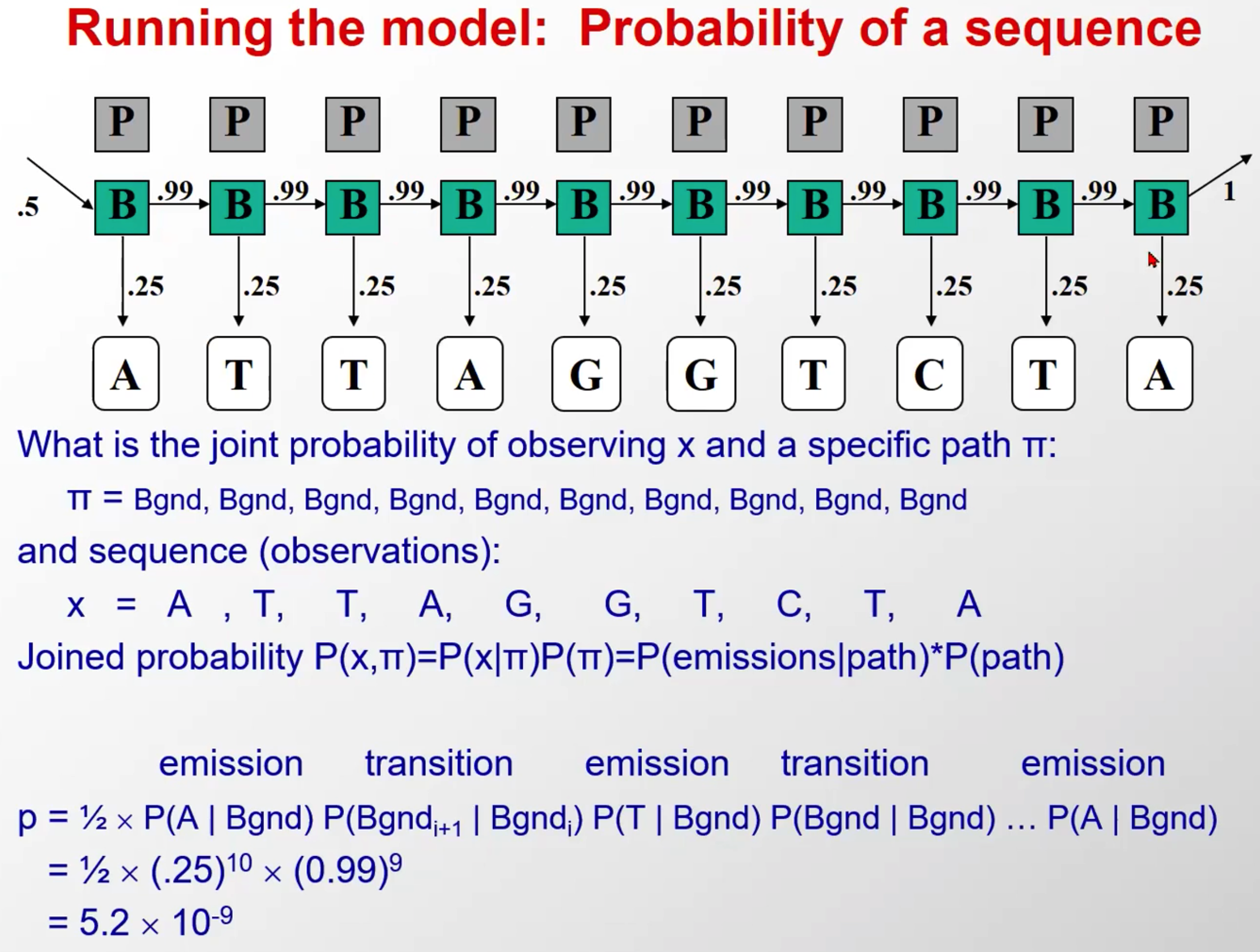
Running the model: Probability of a sequence

其实就是我们前面所说的隐马尔科夫的第一个研究内容，求解观测序列概率估计

在给定隐马尔科夫模型三要素 $\lambda =(A,B,\pi )$的基础上，针对一个具体的观测序列$O=(o1,o2,...,oT)$，求他出现的概率。

这里是举了其中的两种情况，就是另外给出了隐含态序列（实际问题中是不知道的，这是假设），这样我们就可以计算出这个观察态出现的概率，就是初始*每一个转移概率*每一个发射概率

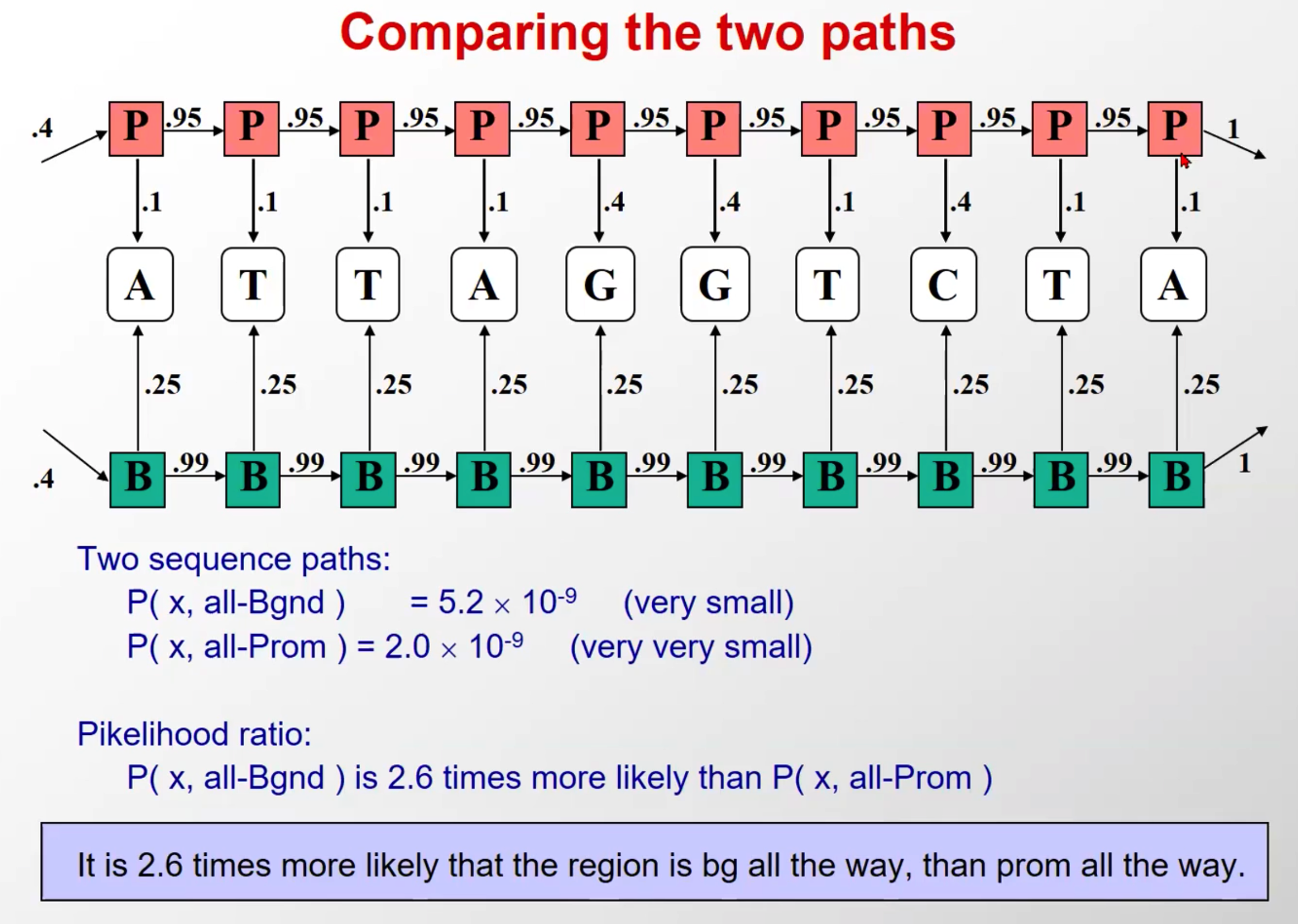
• 进行对比
  • 首先给定该观察序列，然后比较隐含层序列全是background（一种假设）和隐含层序列全是启动子（另一种假设），该观察序列出现的概率前一个是比后一个高的

• 实际上，这种假设是很多的，因为存在转移
  • 这个例子的概率小是因为，多乘上的这俩转移概率比较小（B->P和P->B）

• 我们能够在指定$\lambda =(A,B,\pi )$，针对一个具体的观测序列$O=(o1,o2,...,oT)$和假设的隐含序列$Q=(q1,q2,...,qT)$，求出概率。但是关键的是，要假设的隐含序列太多了，如果暴力枚举的话，开销太大，时间复杂度太高
  • 所以我们要引入动态规划，去找到这个最大联合概率的假设（隐含序列），那样我们就能求出观察序列出现的概率【这段是我的瞎扯，可能理解错了，不需要看，要求第一个研究内容的话应该是用前向算法，第二个内容用动态规划】
• 

维特比算法 Viterbi

这是一种动态规划算法

十分抱歉，由于我的理解错误（my poor English）和被标题误导了，我才发现老师这块教的其实第二个研究内容（所以上一段纯属瞎扯），隐含状态解码，就是给定一个已知的观测序列，求他最有可能对应的状态序列(但是两个内容二者关联性很高，无伤大雅，如果你懂了HMM大概是个啥，就问题不大)

第一个研究内容时求$P(O|\lambda )$最大，第二个研究内容是求$P(I|O,\lambda )$最大

用隐马尔科夫模型的形式化语言概况就是：在给定隐马尔可夫模型三要素$\lambda =(A,B,\pi )$和观测序列$O=(o1,o2,...,oT)$的基础上求使得条件概率$P(I\mid O)$最大（最有可能对应），求的隐藏状态序列 $I=(i_1,i_2,...i_T)$。

一个摸球例子

• 举一段中文的例子，助于理解，注意符号意义不同。理解了递推公式，事情就简单了
  • 隐状态集合$Q=盒子1，盒子2，盒子3$，每个盒子摸出红球和白球概率不同，给出了$\pi 、A、B$

• t1时刻，因为观察序列里是红球$o1$，所以只要初始$\pi$分别乘上对应盒子$o1$的概率

• t2时刻，因为观察序列里是白球$o2$,所以在t2时刻三个盒子的概率可以计算
  • 以t2时刻1号盒子为例子，就是t1时刻的概率（三个盒子）分别乘上对应转移到1号盒子的概率，其中取最大值，然后再乘上1号盒子中抽到白球的概率（发射概率）
  • 为什么说这个方法好呢，因为取了最大值，把另外两种可能性舍弃了，这样就不用考虑这两种的后续

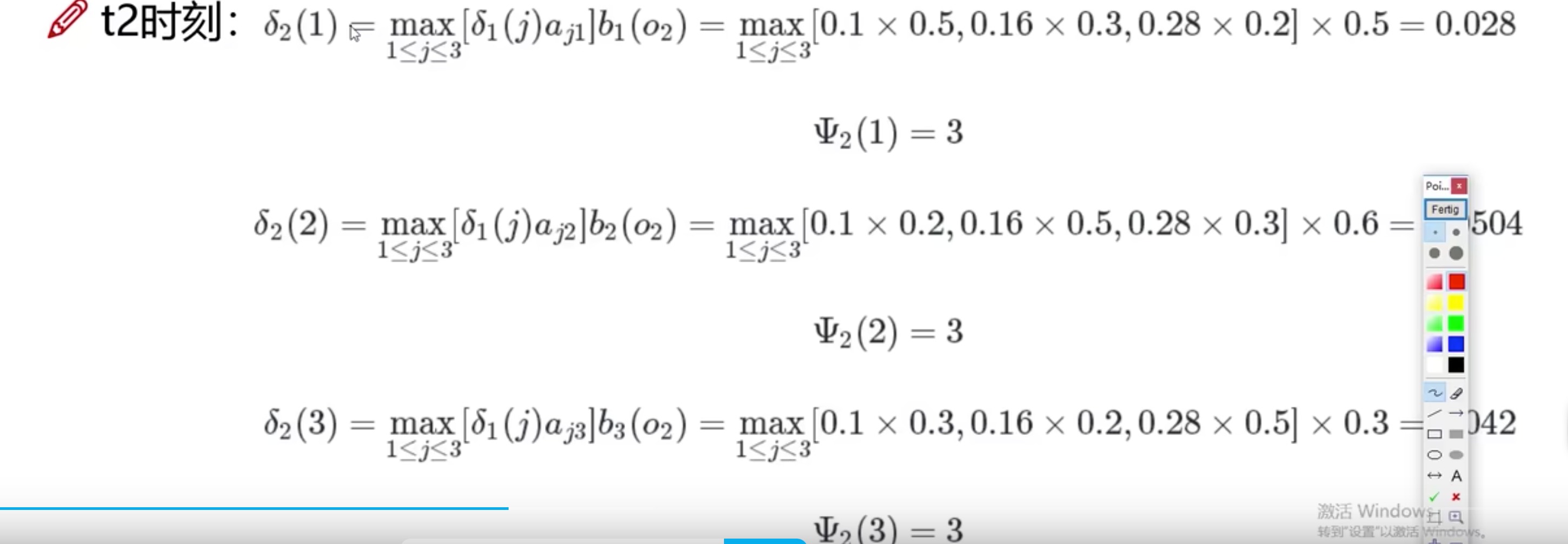
• 解释一下这个是啥，就是存储这三个里最大的状态，最后总结时会用

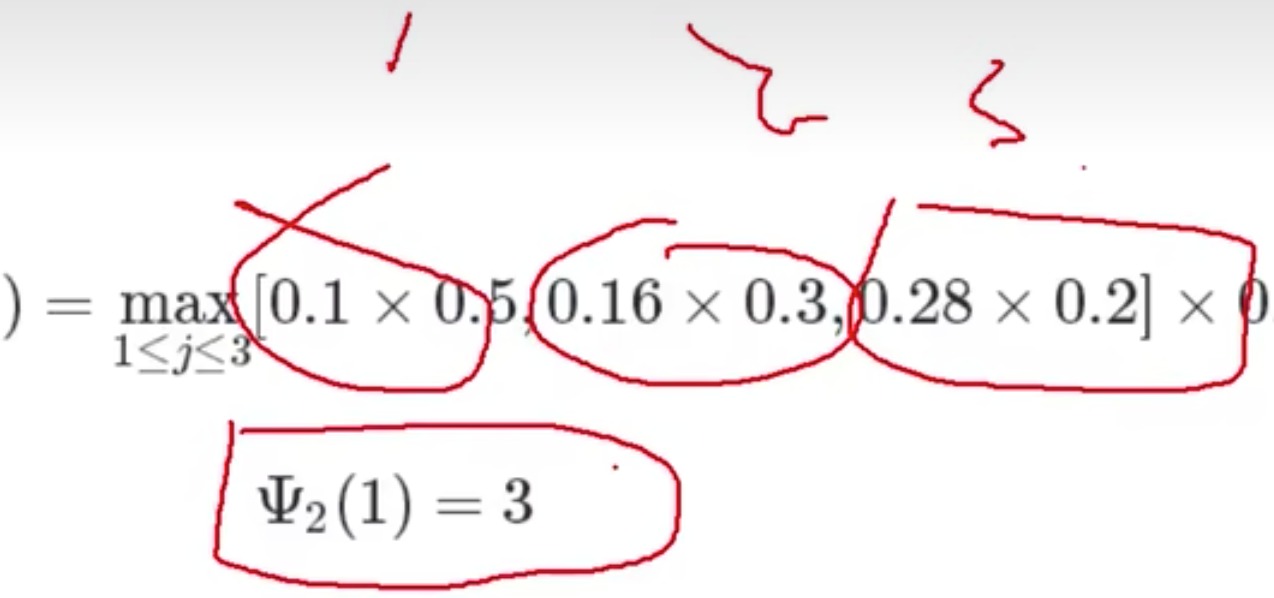
• 然后我们就获得了t3时刻的结果，找最大的可能性

• 我们从前往后先推了一遍，然后找到了最大概率，再倒推找到这条路过来的路径，over

回到课堂

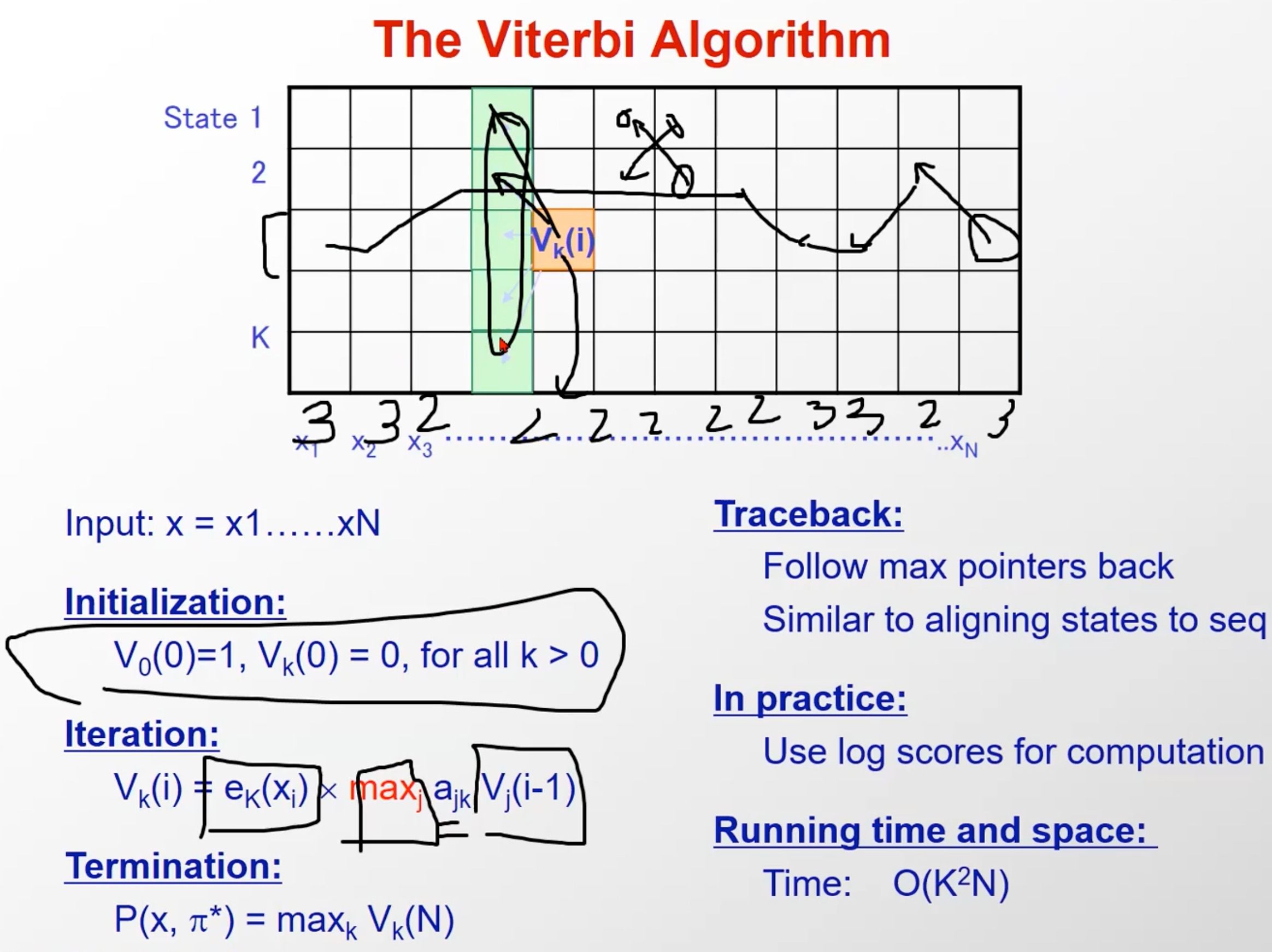
其实就是反应了我们例子中的过程

求解参数

我们发现，以上的问题都给出了$\lambda =(A,B,\pi )$，但是实际问题中这些参数从哪来

• 可以从数据中简单的计算出来

• 事实上，更常见的是啥也不知道，这就是有挑战的地方

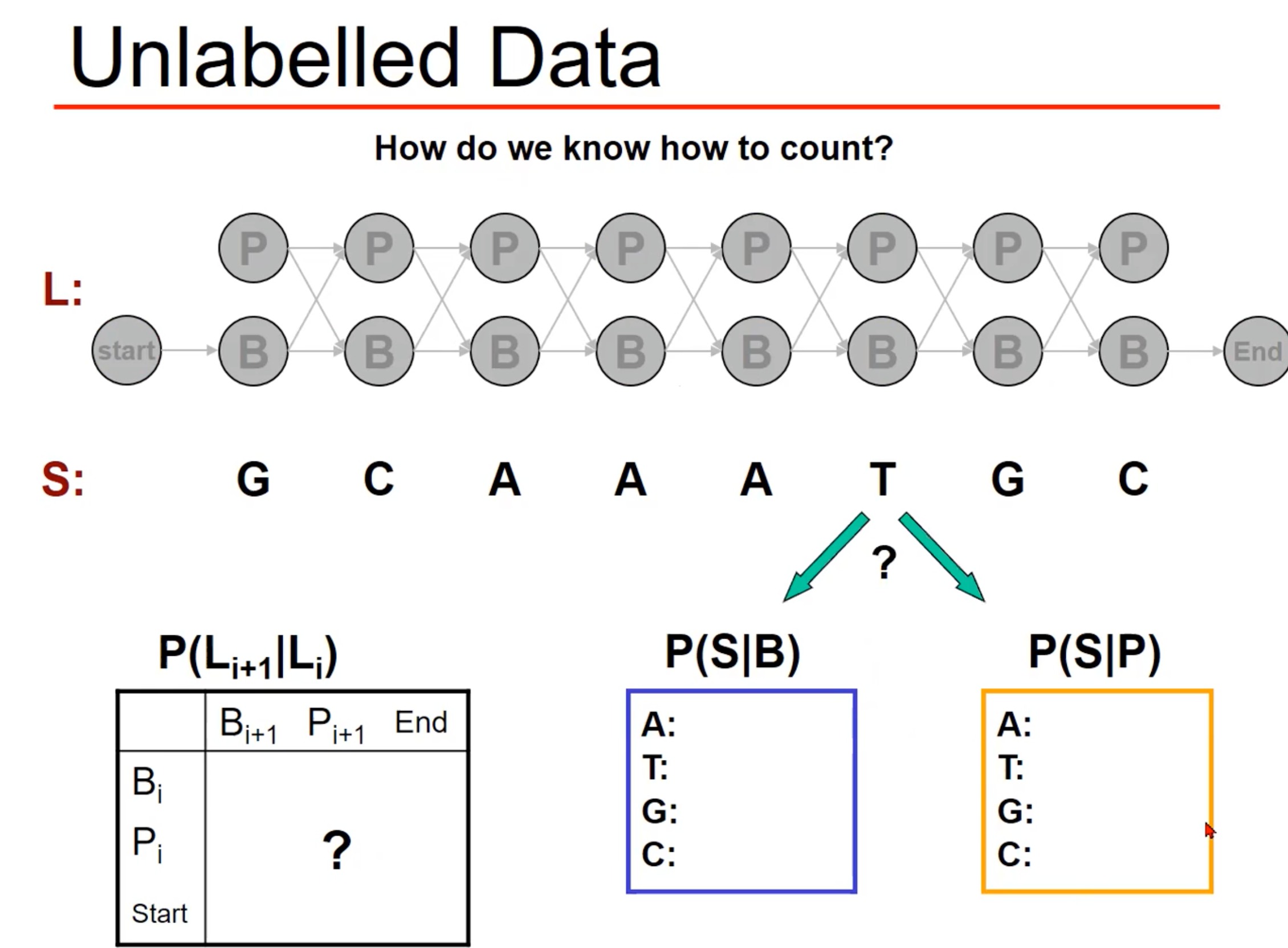
• 其实这是HMM的第三个研究内容，就是求解参数。数学推导比较复杂，其实是采用了EM算法（过程类似于Kmeans），就是不停的迭代，通过极大似然估计找到最佳

• EM

• 

• HMM对于基因组学的意义（by me）

  • 比如根据DNA序列去判断其背后属于哪个state（比如启动子、外显子、内显子等等）

• HMM对于基因组学的意义（by ChatGPT）

  • 基因识别：HMM可以用于基因识别，即从一段基因组序列中找出编码蛋白质的基因序列。在这个过程中，HMM可以使用已知的编码蛋白质的序列信息来训练模型，然后根据这些信息来识别潜在的编码蛋白质基因。
  • DNA序列比对：HMM可以用于比对DNA序列。比对是基因组学中的重要任务之一，它可以帮助研究人员找出不同物种或个体之间的DNA序列差异。HMM可以通过比较两个或多个序列的相似性来实现比对。
  • RNA序列结构预测：HMM可以用于预测RNA序列的结构。RNA序列是基因组学中的重要组成部分，因为它们在基因表达中发挥着重要作用。HMM可以使用RNA序列的已知结构信息来预测新序列的结构。
  • 基因家族分类：HMM可以用于基因家族分类，即将基因根据它们的功能和结构分为不同的家族。这对于理解基因的功能和进化历史至关重要。

• 对应的观察状态和隐含状态（by ChatGPT）

  • 在隐马尔可夫模型中，有两种状态，分别是隐含状态（hidden state）和观察状态（observation state）。
  • 隐含状态表示的是在模型内部的状态，对于观察者来说是不可见的。在基因组学中，隐含状态可以被看作是基因组序列的潜在结构，例如DNA的开放阅读框（open reading frame, ORF）或者RNA的剪接位点。在基因识别和RNA结构预测中，HMM的隐含状态通常表示基因的位置和边界，以及RNA的不同结构状态，例如发夹式结构（hairpin loop）、四联体结构（quadruplex）、外显子和内含子等。
  • 观察状态则表示模型外部可见的状态，也就是我们可以直接观测到的状态。在基因组学中，观察状态通常是基因组序列上的一些特征，例如ATCG碱基序列、RNA序列的二级结构、氨基酸序列等。
  • 因此，在基因组学中，HMM的隐含状态通常表示基因组序列的潜在结构，而观察状态则是基因组序列上的特征。HMM的目标是通过观察状态来推断隐含状态，以便更好地理解基因组序列的功能和结构。