一、三路划分

为何还会有三路划分？

快速排序算法在某个数据大量重复时效率极低，在运行程序时会超出时间限制，为了解决数据大量重复的情况下，三路划分诞生了。三路划分是基于快速排序思想上的，三路划分在于解决数据中有大量重复或者几乎为同一个数据时想出来的，但是对于一般的数据也可以排序。

三路划分思想

三路划分是基于快速排序思想，选出数据中的关键字（随机选数选出关键字），然后对这个关键字(key)进行单趟排序，使小于key的值甩到key的左边，将大于key的值甩到右边，而中间很大一部分区间的值是相同的。中间相等的区间就不用再处理，对这个关键字它的左区间进行相同处理，右区间进行相同处理，对相等值区间不再处理。

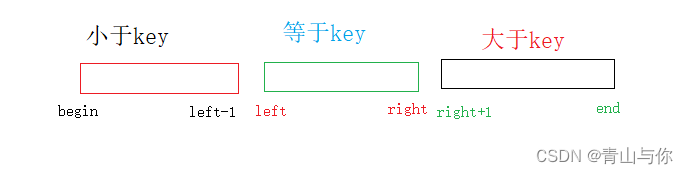
三指针实现，left,cur,right选出关键字如果随机选取之后左边做关键字key=a[left]则从左边走，此时cur = left+1，如果随机选取之后右边做关键字key = a[right]，则cur = right-1,从右边开始走。cur对应得值与关键字key比较，·当a[cur] == key,cur++;当a[cur] < key,就将a[cur]与a[left],此时cur++,left++，当a[cur] > key,将a[right]与a[cur]交换，此时right--,cur不动，由于并不知道交换过来的值是大于还是小于或者等于关键字key，直到cur走到超过right为止。这样一趟排下来会得到区间right - left中的值是相同，区间[begin,left]值小于key,区间[right+1,end]值大于key，这时也就划分为了三个区间（小于、等于、大于）。这样的方法也很类似快排的前后指针法。

一趟排之后划分出三个区间

二、Leetcode912.排序数组

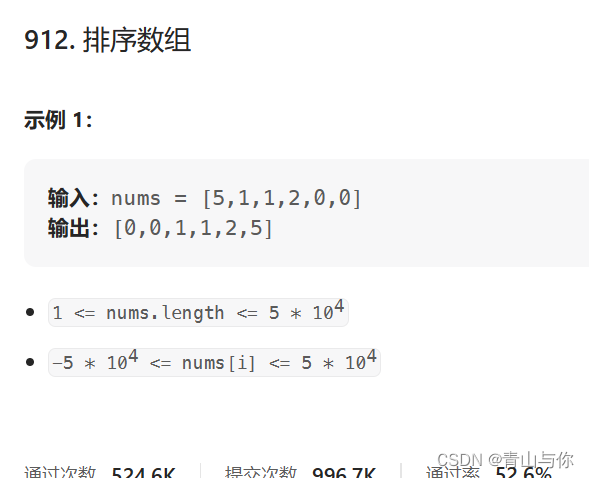
在这里插入图片描述

返回的数组必须是自己malloc出来的

在这里插入图片描述

返回数组首元素地址

在这里插入图片描述

返回的这个数组有多大

用快排三路划分将数组排序

void Swap(int* e1, int* e2)
{
	int tmp = *e1;
	*e1 = *e2;
	*e2 = tmp;
}

void QuickSort(int*a,int left,int right)
{
	//当区间大小为1或者不存在就不需要单趟排序了
    if(left>=right)
    {
        return ;
    }
	//随机选数
    int randi = left + (rand() % (right - left));
	if (randi != left)
	{
		Swap(&a[randi], &a[left]);//以左边做关键值
	}

    int begin = left;
    int key = a[left];//以左边做关键值
    int end = right;
    int cur = left+1;//类似前后指针法

    while(cur<=right)
    {
        if(a[cur] < key)//当前值小于key,交换，两者都向后移动
        {
            Swap(&a[cur], &a[left]);
            cur++;
            left++;
        }

        else if(a[cur]>key)//大于时与最右边的交换，然后right--,
        //由于最开始并不确定a[left]与key关系，所以交换后cur不动
        {
            Swap(&a[cur], &a[right]);
            right--;
        }

        else
        {
            cur++;
        }
    }
    //类似普通快排递归排key值对应区间它的左区间
    QuickSort(a,begin,left-1);
    //递归排key值对应区间它的右区间
    QuickSort(a,right+1,end);
	
	//关键字对应区间不需要处理
}

int* sortArray(int* nums, int numsSize, int* returnSize){
  int*a = (int*)malloc(sizeof(int)*numsSize);
  *returnSize = 0;
   QuickSort(nums,0,numsSize-1);
   //将排好序的数组依次赋值给malloc出来的数组
   for(int i = 0; i<numsSize;i++)
   {
       a[(*returnSize)++] = nums[i];
   }
   
   return a;//返回malloc出来的数组a的首地址
}