单纯、混合进制通吃,真正的黄金万能的进制转换方法。
-
Python 官网:https://www.python.org/
-
Free:大咖免费“圣经”教程《 python 完全自学教程》,不仅仅是基础那么简单……
地址:https://lqpybook.readthedocs.io/
自学并不是什么神秘的东西,一个人一辈子自学的时间总是比在学校学习的时间长,没有老师的时候总是比有老师的时候多。
—— 华罗庚
- My CSDN主页、My HOT博、My Python 学习个人备忘录
- 好文力荐、 老齐教室

-
Python 官网:https://www.python.org/
-
Free:大咖免费“圣经”教程《 python 完全自学教程》,不仅仅是基础那么简单……
地址:https://lqpybook.readthedocs.io/
自学并不是什么神秘的东西,一个人一辈子自学的时间总是比在学校学习的时间长,没有老师的时候总是比有老师的时候多。
—— 华罗庚
- My CSDN主页、My HOT博、My Python 学习个人备忘录
- 好文力荐、 老齐教室

本文质量分:
CSDN质量分查询入口:http://www.csdn.net/qc
- ◆X进制转换十进制黄金万能算法
- 0、“算法”诞生的契机
- 1、X 进制减法
- 1.0 问题描述
- 1.1 解题思路
- 1.2 我入了常规进制的“坑”
- 1.2.1 手动演算
- 1.2.2 自拟代码演算
- 1.2.3 Python内置转整函数 int() 演算
- 1.3 我“醒豁”了
- 1.4 X进制转十进制的“黄金算法”——万能算法
- 1.5 求得正解😎
- 2、“黄金”万能算法解析
- 2.1 进制转换的基本“原理”(常规)
- 2.2 确定数位倍率
- 2.3 数位数值与对应倍率配对
- 3、我的感悟
- 4、我曾经记下的稚嫩进制转换笔记
◆X进制转换十进制黄金万能算法
0、“算法”诞生的契机
我在用 Python 代码“抽丝剥茧”十三届蓝桥杯省赛 C/C++大学 B 组赛题第五题时,对于算法“始终不得要领”,后摸索求着得正解,但所用“算法”原理,连我自己都不能明了。我本着一贯爱钻牛角尖尖的“精神”,对其“日夜相思”,最终不负所“爱”,窃得“黄金万能”的进制转换“算法”。
本着“好东西不敢私藏”的一贯“追求”,留此博文笔记,以资共享。😜😜🤪🤪
如果想对我要讲的“算法”,有更明晰的理解基础,可以接下来先看看 十三届蓝桥杯省赛 C/C++大学 B 组赛题第五题:“ X 进制减法” 的解题过程,沉入我当时“不得要领”的混沌时空,一个不小心就可能开启您的顿悟,比我更快明白“黄金万能”进制转换算法哩。🤗
当然,您也可以点击跳转直接略过。
1、X 进制减法
1.0 问题描述
进制规定了数字在数位上逢几进一。
X 进制是一种很神奇的进制,因为其每一数位的进制并不固定!例如说某种 X 进制数,最低数位为二进制,第二数位为十进制,第三数位为八进制,则 X 进制数 3 2 1 转换为十进制数为 65 。
现在有两个 X 进制表示的整数 A 和 B,但是其具体每一数位的进制还不确定,只知道 A 和 B 是同一进制规则,且每一数位最高为 N 进制, 最低为二进制。请你算出 A−B 的结果最小可能是多少。
请注意:你需要保证 A 和 B 在 X 进制下都是合法的,即每一数位上的数字要小于其进制。
- 输入格式
第一行一个正整数 N,含义如题面所述。
第二行一个正整数 Ma,表示 X 进制数 A 的位数。
第三行 Ma 个用空格分开的整数, 表示 X 进制数 A 按从高位到低位顺序各个数位上的数字在十进制下的表示。
第四行一个正整数 Mb, 表示 X 进制数 B 的位数。
第五行 Mb 个用空格分开的整数,表示 X 进制数 B 按从高位到低位顺序各个数位上的数字在十进制下的表示。
请注意:输入中的所有数字都是十进制的。
- 输出格式
输出一行一个整数,表示 X 进制数 A−B 的结果的最小可能值转换为十进制后再模 1000000007 的结果。
- 样例
输入
11
3
10 4 0
3
1 2 0
输出
94
- 样例说明
当进制为:最低位 2 进制,第二数位 5 进制, 第三数位 11 进制时,减法得到的差最小。此时 A 在十进制下是 108,B 在十进制下是 14,差值是 94。
- 评测用例规模与约定
对于 30% 的数据, N ≤ 10; Ma, Mb ≤ 8;
对于 100% 的数据,2 ≤ N ≤ 1000; 1 ≤ Ma, Mb ≤ 100000; A ≥ B.
- 运行限制
最大运行时间:1s
最大运行内存:256M
1.1 解题思路
据题意,要使X进制整数 a - b 的值最小,则被减数 a 要用合适的“进制序列”令其值最小。依“满则向左边高位进 1 ”(进制规定了数字在数位上逢几进一)的进制规则可知,X进制整数 a ,每个数位都处于进位临界值——比进制小 1 ——时,其值最小。因而 a 的“最适”进制序列即为对应数位上的值 + 1 ,b 的进制依 a ( A 和 B 是同一进制规则),按 a 的进制序列求出 a、b 的十进制值,返回差值。
1.2 我入了常规进制的“坑”
常规进制求值(十进制值)算法,从低位到高位,依次求取“数位值×进制^数位索引”,如:
十进制整数:“2 0 5” = 5×10^0 + 0×10^1 + 2×10^2 = 5 + 0 + 200
二进制整数:“1 1 1” = 1×2^0 + 1×2^1 + 1×2^2 = 1 + 2 + 4
题目中说,“例如说某种 X 进制数,最低数位为二进制,第二数位为十进制,第三数位为八进制,则 X 进制数 321 转换为十进制数为 65 。”
十进制数位值 3 2 1
X 进制序列 8 10 2
其十进制值 1 + 2×2^1 + 3×10^2 = 1 + 4 + 300
X进制整数“3 2 1”怎么不是 65 而是 305 ?照此“逻辑”,“10 4 0”、“1 2 0”也得不出 108 和 14 !!
a 十进制数位值 10 4 0
X 进制序列 11 5 2
其十进制值 0 + 4×2^1 + 10×5^2 = 0 + 8 + 250
b 十进制数位值 1 2 0
其十进制值 0 + 2×2^1 + 1×5^2 = 0 + 4 + 25
求X进制整数十进制值的函数 (按常规进制——“单纯”进制,各数位仅有一种进制的整数算法)
def get_value(name: str, x: str, x_n: int, multiples: list) -> int: # 返回十进制整数。
''' 求X进制数的十进制值(算法入坑,不对) '''
result = 0
print(f"\n{name}进制整数:'{x}'\n{'':~^50}\n")
x = list(map(int, x.split())) # 列表解析将字符串数字转换整型。
x = [x.pop() for i in x[:]] # 列表解析倒置X进制整数序列。
multiples = [1] + [multiples[i-1] for i in range(x_n, 0, -1)] # 切片倒置X进制列表。
#input((x, multiples)) # 调试用语句。
result = 0 # 结果初值。
for index,i in enumerate(zip(x, multiples)):
result += i[0]*i[1]**index
print(f"进制:{i[1] if index else 'None'},倍率:{i[1]**index},数位/值:{index+1}/{i[0]},十进制值:{i[0]*i[1]**index}")
print(f"\n{name}进制整数的十进制值是:{result}\n{'':~^50}")
return result
代码运行效果截屏
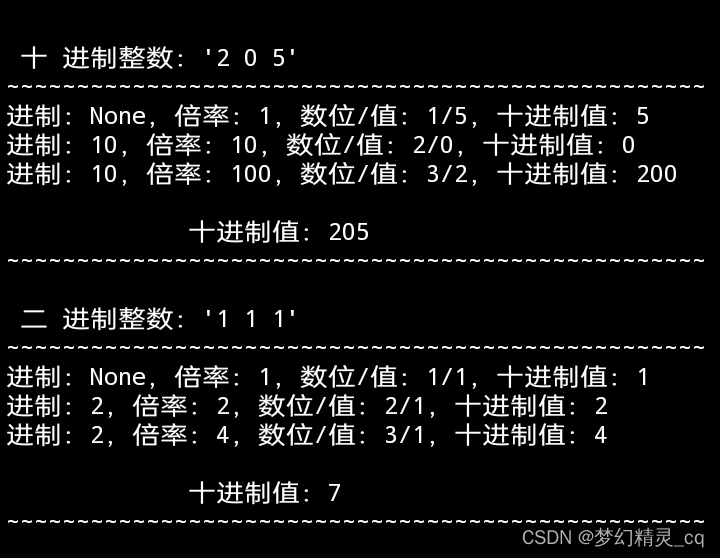

以计算X进制整数“222”,从3进制到11进制的十进制值来进行“算法”验证:
1.2.1 手动演算
十进制数位值 2 2 2
X 进制序列 3 3 3
其十进制值 2×3^0 + 2×3^1 + 2×3^2 = 2 + 6 + 18
…
X 进制序列 11 11 11
其十进制值 2×11^0 + 2×11^1 + 2×11^2 = 2 + 22 + 242
1.2.2 自拟代码演算
- 代码演算一 (调用自码X进制求值——十进制——函数 get_value() )
if __name__ == '__main__':
x_s = '2 2 2'
print(f"\n X 进制整数“{x_s}”,分别是 3~11 进制时的十进制值:\n{'':~^50}\n")
for i in range(3, 12):
get_value(str(i), x_s, 3, [i]*3)
代码演算截屏
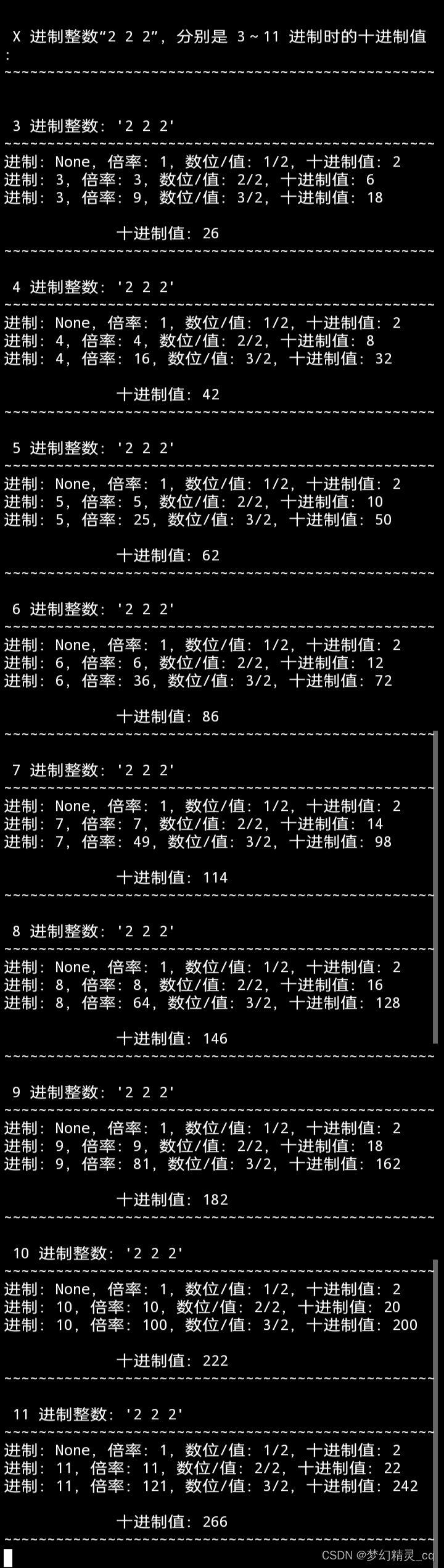
1.2.3 Python内置转整函数 int() 演算
- 代码演算二 (Python的字符型数字转整型函数int())
/sdcard/qpython $ python
Python 3.11.1 (main, Dec 7 2022, 05:56:18) [Clang 14.0.6 (https://android.googlesource.com/toolchain/llvm-project 4c603efb0 on linux
Type "help", "copyright", "credits" or "license" for more information.
>>>
>>> s = '222'
>>> for i in range(3, 12):
... print(f" {i} 进制整数 '{s}' 的十进制值:{int(s, i)}")
...
3 进制整数 '222' 的十进制值:26
4 进制整数 '222' 的十进制值:42
5 进制整数 '222' 的十进制值:62
6 进制整数 '222' 的十进制值:86
7 进制整数 '222' 的十进制值:114
8 进制整数 '222' 的十进制值:146
9 进制整数 '222' 的十进制值:182
10 进制整数 '222' 的十进制值:222
11 进制整数 '222' 的十进制值:266
>>>
经Python转整函数 int() 验证,“我的算法”对于单一进制的正整数,是完全“正确的”。但这常规进制“算法”,对混合进制数位的X进制整数为什么就无效了呢?🤨
1.3 我“醒豁”了
经过细心观察省度,我“窥得门径”,代码可以正确求取X进制整数的十进制值了——
def get_value(name: str, x: str, x_n: int, multiples: list) -> int: # 返回十进制整数。
''' 求X进制数的十进制值(破坑而出还是坑) '''
result = 0
print(f"\n{name}进制整数:'{x}'\n{'':~^50}")
x = list(map(int, x.split())) # 列表解析将字符串数字转换整型。
x = [x.pop() for i in x[:]] # 列表解析倒置X进制整数序列。
multiples = [1] + [multiples[i-1] for i in range(x_n, 0, -1)] # 切片倒置X进制列表。
result = 0 # 结果初值。
for index,i in enumerate(zip(x, multiples)):
if index == 0:
result += i[0]
else:
result += i[0]*(i[1]*index)
print(f"进制:{i[1] if index else 'None'},倍率:{i[1]*index if index else 1},数位/值:{index+1}/{i[0]},十进制值:{i[0]*index}")
print(f"\n{name}进制整数的十进制值是:{result}\n{'':~^50}")
return result
得出了X进制整数解析十进制值的正确结果😁

但算法似乎“没有依仗”,我自己都不能自圆其说。🤣
且这算法仅可解析混合多进制数位的X进制整数,对常规单一进制整数无效。
但我理不清“算法思想”,这醒豁是个伪命题。😂且调用函数处理前面列举的“2 2 2”字符解析分别为3~11进制时,对应的十进制值,是不正确的。

这“算法”不真!!还待考究。
我这是根本就没有拨开迷雾,走出跌入的坑。🧐🧐
1.4 X进制转十进制的“黄金算法”——万能算法
经过对算法反复推敲,仔细示例验证,终究是得出了适用常规和刁钻的进制组合整数能吃的“黄金万能”算法。😎😎
先丢出转换函数代码,然后再 逐一剖析“注释”代码。
转换函数代码
def get_value(name: str, x: str, x_n: int, multiples: list) -> int: # 返回十进制整数。
''' 求 X 进制整数的十进制值(“真算法”) '''
result = 0
print(f"\n {name} 进制整数:'{x}'\n{'':~^50}")
x = list(map(int, x.split())) # 列表解析将字符串数字转换整型。
x = [x.pop() for i in x[:]] # 列表解析倒置X进制整数序列。
multiples = ['None'] + [multiples[i-1] for i in range(x_n, 0, -1)] # 切片倒置X进制列表,并前补一项 1 。
result = 0 # 结果初值。
for index,i in enumerate(zip(x, multiples)):
if index == 0:
result += i[0]
multiple = 1
else:
multiple *= i[1]
result += i[0]*multiple
print(f"进制:{i[1] if index else 'None'},倍率:{multiple},数位/值:{index+1}/{i[0]},十进制值:{i[0]*multiple}")
print(f"\n{'十进制值:':>18}{result}\n{'':~^50}")
return result
重算前面的例子:

本题目中的三个X进制整数:“3 2 1”、“10 4 0”、“1 2 0”

由截屏图片可鉴,不管是学“常规进制”还是刁钻的 X 进制整数,调用“万能黄金算法”函数,都可以得到正确的十进制值。😎😎
嚯!!还真没白瞎我对此题目的“日思夜想”😜😜(欲了解算法详情,请点按蓝色文字跳转翻阅)。
1.5 求得正解😎
调用函数求解代码
if __name__ == '__main__':
print(f"\nV、X进制减法\n{'':~^50}")
s = '''
11
3
10 4 0
3
1 2 0
'''
print(f"\n输入:{s}")
input_s =[int(i) if i.isdigit() else i for i in s.split('\n')[1:-1]]
print(f"\n\n输出:\n{x_subtraction(input_s)}")
运行效果截图(我已打印出运算过程,对算法就不再作讲解,欲了解算法解析,请点按蓝色文字跳转翻阅)

2、“黄金”万能算法解析
2.1 进制转换的基本“原理”(常规)
进制转换的基本“原理”:
- 依次求取每个数位的数值,取其总和,即是所要求取的最终结果。
- 为方便代码操作,一般从低位到高位遍历轮询。
- 为方便遍历轮询操作,一般先将高低数位倒置。
可以用负数步长切片或者 list.pop() 模拟栈弹出来实现整数数位“倒置”。
如对 X 进制整数 “3 2 1” 倒置:
负数步长切片
>>>
>>> s = '3 2 1'.split()
>>> n = len(s)
>>> s1 = [s[i] for i in range(-1, -n-1, -1)]
>>> s1
['1', '2', '3']
>>>
list.pop()
>>> s = '3 2 1'.split()
>>> s2 = [s.pop() for i in s[:]]
>>> s2
['1', '2', '3']
>>>
“倒置”原理:负数步长遍历轮询,即是从后往前取序列元素;list.pop() 默认返回删除的最后一个列表元素(给定下标参数则返回删除的指定下标元素)。
2.2 确定数位倍率
要求得各数位上十进制对应数值,只要求得数位倍率,与数位上的数字相乘之积,即为当前数位的对应的十进制值。
“纯”进制整数:

“ X ”进制整数:


- 最低位的倍率都是“ 1 ”。
如前面列举的单纯进制整数示例,最低位倍率为进制的0次幂,即 1 ( 0 以外的任何数的 0 次幂都是 1 )。最低位十进制值就等于数位数字。算法代码如下:
for index,i in enumerate(zip(x, multiples)):
if index == 0:
result += i[0]
- 次低位的进制倍率为最低位进制。
for index,i in enumerate(zip(x, multiples)):
if index == 0:
result += i[0]
multiple = i[1]
- 其余数位进制倍率为比其低的数位不含本数位进制)所有进制之积。
如紧邻次低位的第三数位,其倍率为 最低位进制 × 次低位进制,如代码:
else:
multiple *= i[1]
result += i[0]*multiple
2.3 数位数值与对应倍率配对
不难发现,我们要计算的数位数值与数位进制错开一个数位,这给代码实现造成了障碍。数位数值(数位数字)与对应的数位倍率配对,才可以方便计算。
这难不倒有准备的人,用 list.insert() 方法或者 + 运算符(列表连接运算符),可以达成目的。

经“命令行模式”试炼, list.insert() 方法与“ + ” list 列表连接运算符效果相同,但后者语法更为简洁明了。
/sdcard/qpython $ python
Python 3.11.1 (main, Dec 7 2022, 05:56:18) [Clang 14.0.6 (https://android.googlesource.com/toolchain/llvm-project 4c603efb0 on linux
Type "help", "copyright", "credits" or "license" for more information.
>>>
>>> s = '3 2 1'
>>> s = list(map(int, s.split()))
>>> s = [s.pop() for i in s[:]] # 数位倒置。
>>> multiples1 = ['None'] + [2, 10, 8] # 进制序列 已倒置。
>>>
>>> multiples2 = [2, 10, 8]
>>> multiples2.insert(0, 'None')
>>>
>>> multiples1, multiples2
(['None', 2, 10, 8], ['None', 2, 10, 8])
>>>
zip() 函数实施数位数值与计算“适用”进制配对
>>>
>>> temp = list(zip(s, multiples1))
>>> temp2 = list(zip(s, multiples2))
>>> temp, temp2
([(1, 'None'), (2, 2), (3, 10)], [(1, 'None'), (2, 2), (3, 10)])
>>>
3、我的感悟
“代码是程序的身躯,算法是程序的灵魂”,选择最适算法,才会让程序更具灵性。
比如本笔记前面的示例:纯进制整数,可以进制幂次方也可以选择乘积,但混合 X 进制整,却不可以选择那种“不可名状”的算法,虽然也可以结果正确。
4、我曾经记下的稚嫩进制转换笔记
- 十六进制字符串转Python代码(utf-8字符串转十六进制字符串)
( 1810 阅读)
地址:https://blog.csdn.net/m0_57158496/article/details/126336904
点赞:4 踩 :0 收藏:8 打赏:0 评论:5
本篇博文笔记于 2022-08-14 22:12:32 首发,最晚于 2022-08-24 09:16:59 修改。 - 练习:自撸整数进制转换器(二、八、十六进制转十进制)
( 647 阅读)
地址:https://blog.csdn.net/m0_57158496/article/details/123079272
点赞:1 踩 :0 收藏:1 打赏:0 评论:1
本篇博文笔记于 2022-02-22 22:52:14 首发,最晚于 2022-02-23 11:55:52 修改。
上一篇: x in ‘Yy’ == x in list(‘Yy’)?(空字符串 ‘’ 是任何字符串的子串)
下一篇:
我的HOT博:
本次共计收集 196 篇博文笔记信息,总阅读量 30.94w,平均阅读量 1578。已生成 18 篇阅读量不小于 3000 的博文笔记索引链接。数据采集于 2023-04-15 07:53:23 完成,用时 4 分 19.18 秒。
- 让QQ群昵称色变的神奇代码
( 52785 阅读)
博文地址:https://blog.csdn.net/m0_57158496/article/details/122566500
点赞:22 踩 :0 收藏:74 打赏:0 评论:16
本篇博文笔记于 2022-01-18 19:15:08 首发,最晚于 2022-01-20 07:56:47 修改。 - ChatGPT国内镜像站初体验:聊天、Python代码生成等
( 43956 阅读)
博文地址:https://blog.csdn.net/m0_57158496/article/details/129035387
点赞:121 踩 :0 收藏:781 打赏:0 评论:73
本篇博文笔记于 2023-02-14 23:46:33 首发,最晚于 2023-03-22 00:03:44 修改。 - pandas 数据类型之 DataFrame
( 7771 阅读)
博文地址:https://blog.csdn.net/m0_57158496/article/details/124525814
点赞:6 踩 :0 收藏:23 打赏:0 评论:0
本篇博文笔记于 2022-05-01 13:20:17 首发,最晚于 2022-05-08 08:46:13 修改。 - 罗马数字转换器|罗马数字生成器
( 6263 阅读)
博文地址:https://blog.csdn.net/m0_57158496/article/details/122592047
点赞:0 踩 :0 收藏:1 打赏:0 评论:0
本篇博文笔记于 2022-01-19 23:26:42 首发,最晚于 2022-01-21 18:37:46 修改。 - Python字符串居中显示
( 5897 阅读)
博文地址:https://blog.csdn.net/m0_57158496/article/details/122163023
点赞:1 踩 :0 收藏:5 打赏:0 评论:1
本篇博文笔记于 2021-12-26 23:35:29 发布。 - 斐波那契数列的递归实现和for实现
( 5251 阅读)
博文地址:https://blog.csdn.net/m0_57158496/article/details/122355295
点赞:4 踩 :0 收藏:2 打赏:0 评论:8
本篇博文笔记于 2022-01-06 23:27:40 发布。 - 练习:字符串统计(坑:f‘string‘报错)
( 4830 阅读)
博文地址:https://blog.csdn.net/m0_57158496/article/details/121723096
点赞:0 踩 :0 收藏:1 打赏:0 评论:0
本篇博文笔记于 2021-12-04 22:54:29 发布。 - 练习:尼姆游戏(聪明版/傻瓜式•人机对战)
( 4538 阅读)
博文地址:https://blog.csdn.net/m0_57158496/article/details/121645399
点赞:14 踩 :0 收藏:42 打赏:0 评论:0
本篇博文笔记于 2021-11-30 23:43:17 发布。 - 回车符、换行符和回车换行符
( 4257 阅读)
博文地址:https://blog.csdn.net/m0_57158496/article/details/123109488
点赞:0 踩 :0 收藏:2 打赏:0 评论:0
本篇博文笔记于 2022-02-24 13:10:02 首发,最晚于 2022-02-25 20:07:40 修改。 - python清屏
( 4110 阅读)
博文地址:https://blog.csdn.net/m0_57158496/article/details/120762101
点赞:0 踩 :0 收藏:5 打赏:0 评论:0
本篇博文笔记于 2021-10-14 13:47:21 发布。 - 个人信息提取(字符串)
( 4038 阅读)
博文地址:https://blog.csdn.net/m0_57158496/article/details/124244618
点赞:1 踩 :0 收藏:8 打赏:0 评论:0
本篇博文笔记于 2022-04-18 11:07:12 首发,最晚于 2022-04-20 13:17:54 修改。 - 密码强度检测器
( 3809 阅读)
博文地址:https://blog.csdn.net/m0_57158496/article/details/121739694
点赞:1 踩 :0 收藏:4 打赏:0 评论:0
本篇博文笔记于 2021-12-06 09:08:25 首发,最晚于 2022-11-27 09:39:39 修改。 - 罗马数字转换器(用罗马数字构造元素的值取模实现)
( 3757 阅读)
博文地址:https://blog.csdn.net/m0_57158496/article/details/122608526
点赞:0 踩 :0 收藏:0 打赏:0 评论:0
本篇博文笔记于 2022-01-20 19:38:12 首发,最晚于 2022-01-21 18:32:02 修改。 - 练习:班里有人和我同生日难吗?(概率probability、蒙特卡洛随机模拟法)
( 3484 阅读)
博文地址:https://blog.csdn.net/m0_57158496/article/details/124424935
点赞:1 踩 :0 收藏:2 打赏:0 评论:0
本篇博文笔记于 2022-04-26 12:46:25 首发,最晚于 2022-04-27 21:22:07 修改。 - 练习:生成100个随机正整数
( 3369 阅读)
博文地址:https://blog.csdn.net/m0_57158496/article/details/122558220
点赞:1 踩 :0 收藏:3 打赏:0 评论:0
本篇博文笔记于 2022-01-18 13:31:36 首发,最晚于 2022-01-20 07:58:12 修改。 - 我的 Python.color() (Python 色彩打印控制)
( 3246 阅读)
博文地址:https://blog.csdn.net/m0_57158496/article/details/123194259
点赞:2 踩 :0 收藏:7 打赏:0 评论:0
本篇博文笔记于 2022-02-28 22:46:21 首发,最晚于 2022-03-03 10:30:03 修改。 - 练习:仿真模拟福彩双色球——中500w巨奖到底有多难?跑跑代码就晓得了。
( 3131 阅读)
博文地址:https://blog.csdn.net/m0_57158496/article/details/125415626
点赞:3 踩 :0 收藏:4 打赏:0 评论:3
本篇博文笔记于 2022-06-22 19:54:20 首发,最晚于 2022-06-23 22:41:33 修改。 - 聊天消息敏感词屏蔽系统(字符串替换 str.replace(str1, *) )
( 3006 阅读)
博文地址:https://blog.csdn.net/m0_57158496/article/details/124539589
点赞:3 踩 :0 收藏:3 打赏:0 评论:3
本篇博文笔记于 2022-05-02 13:02:39 首发,最晚于 2022-05-21 06:10:42 修改。

精品文章:
- 好文力荐:齐伟书稿 《python 完全自学教程》 Free连载(已完稿并集结成书,还有PDF版本百度网盘永久分享,点击跳转免费🆓下载。)
- OPP三大特性:封装中的property
- 通过内置对象理解python'
- 正则表达式
- python中“*”的作用
- Python 完全自学手册
- 海象运算符
- Python中的 `!=`与`is not`不同
- 学习编程的正确方法
来源:老齐教室
◆ Python 入门指南【Python 3.6.3】
好文力荐:
-
全栈领域优质创作者——寒佬(还是国内某高校学生)博文“非技术文—关于英语和如何正确的提问”,“英语”和“会提问”是学习的两大利器。
-
【8大编程语言的适用领域】先别着急选语言学编程,先看它们能干嘛
-
靠谱程序员的好习惯
CSDN实用技巧博文:
- 8个好用到爆的Python实用技巧
- python忽略警告
- Python代码编写规范
- Python的docstring规范(说明文档的规范写法)
![[Netty源码] 服务端启动过程 (二)](https://img-blog.csdnimg.cn/09ce0283fb784650a30d1b442018e098.png)