( gallery problem or museum problem )
Art gallery problem - Wikipedia
一、说明
画廊问题是一个基本的计算几何问题,最现实的反映是,到底对一个场景监视会用到几个摄像头。更深刻的层次是,如何对场景生成地图,或机器人对地理环境的理解。本文将叙述一个简单经典问题的提出和解决,用于增强理论修养。
二、博物馆问题简述
艺术画廊问题或博物馆问题是计算几何中一个经过充分研究的可见性问题。它源于以下现实世界的问题:
“在一个艺术馆里,最少有多少守卫可以一起观察整个画廊?”在问题的几何版本中,美术馆的布局由一个简单的多边形表示,每个守卫由多边形中的一个点表示。一套如果对于每个点,则称点 S 保护多边形p 在多边形中,有一些∈q\in S 使得线段之间和q 不离开多边形。
当人工智能 (AI) 需要根据周围环境执行动作时,美术馆问题可以应用于多个领域,例如机器人技术。应用此问题的其他领域包括图像编辑、舞台照明问题或用于自然灾害预警的基础设施安装。
原始问题有许多变体,也称为美术馆问题。在某些版本中,守卫被限制在周边,甚至是多边形的顶点。一些版本只需要保护周边或周边的子集。
解决必须在顶点上放置守卫且只需要守卫顶点的版本,相当于解决多边形可见图上的支配集问题。
三、关于三角剖分
3.1 三角剖分:triangulation argigoth
顾名思义,三角剖分(triangulation)就是对给定的平面点集,生成三角形集合的过程。考虑平面点集P={ p1...pk },我们希望得到三角形集合T=在{ t1...ts },满足:
- a)所有三角形的端点恰好构成集合P。
- b)任意两个三角形的边不相交(要么重合,要么没有交点)。
- c)所有三角形的合集构成P的凸包(convex hull)。
3.2 三角剖分不唯一
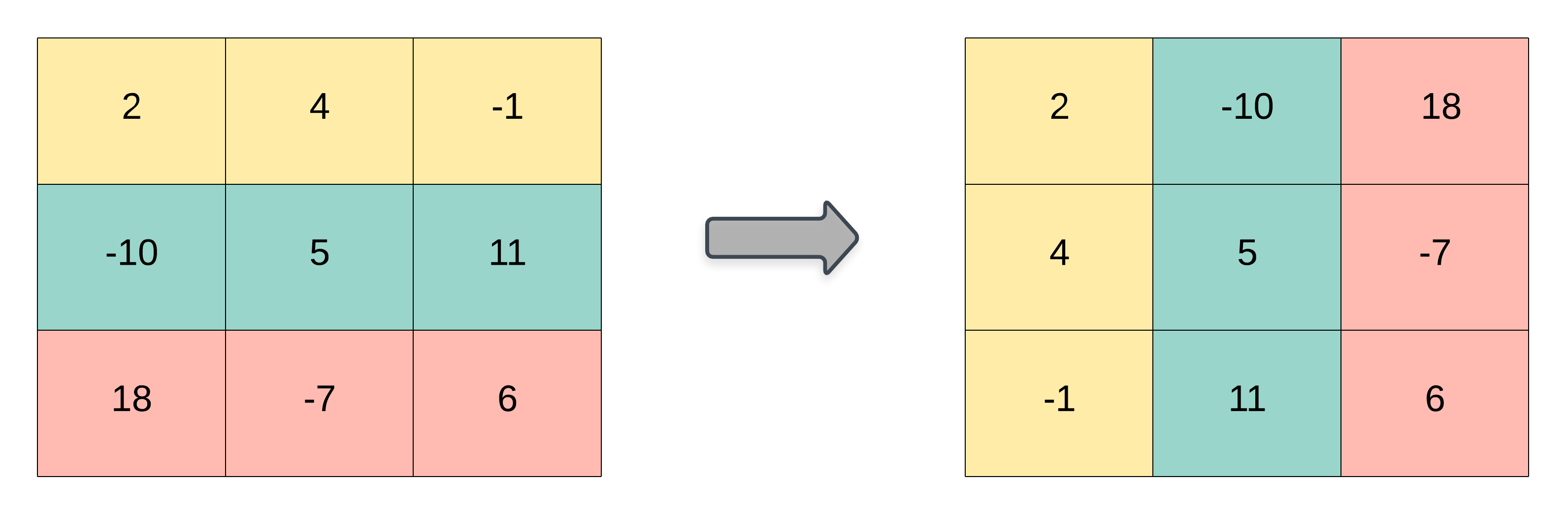
一般来说给定一个点集,往往存在不止一个三角剖分。以下图为例,我们只要把第一个三角剖分中的两个相邻三角形的公共边做一次翻转,就可以得到一个新的三角剖分。
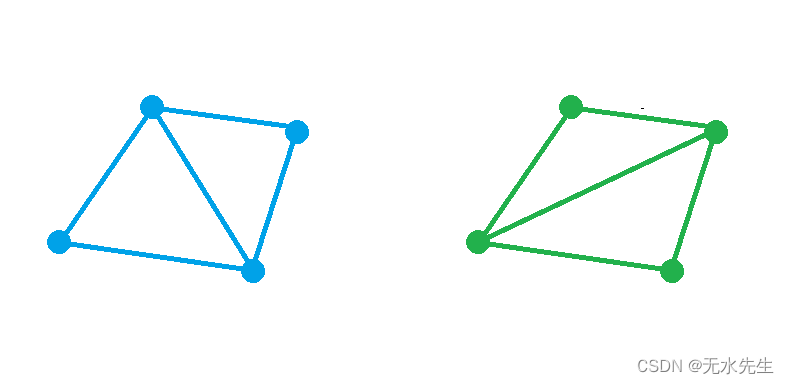
三角刨分不唯一。
四、回到博物馆问题
4.1 博物馆问题
左边博物馆的守卫可以从他的位置看到所有的点。毫无疑问,若博物馆地图有N个顶点,部署N个守卫肯定能监视博物馆全部地界。然而,能否用最少的守卫监视整个博物馆?因此,引出一个多边形的三角抛分问题。
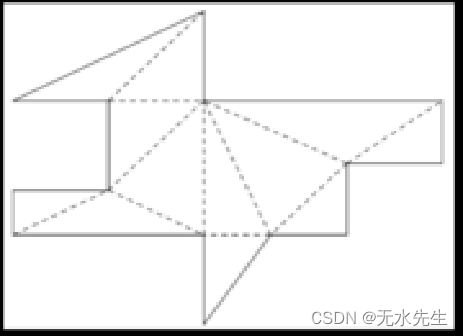
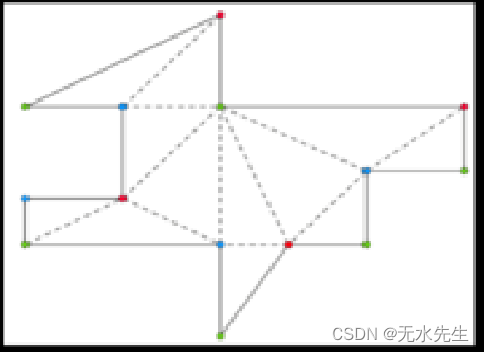
经过三角抛分后,每个三角形取出一个顶点就可以监视全部博物馆,因此,守卫人数可以少于N/3个完成监视任务。
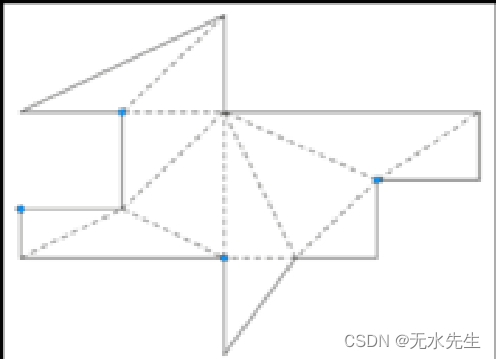
4.2 涂色问题
下图是一个三角抛分后的涂色问题
4.3 证明问题
1975 年,Chvatal 发表的论文 [1] 表明画廊问题可以通过 n⌊ 3 个哨兵来完整监视,且有时 ⌊ n 3 ⌋ 个哨兵是必要的。但是其证明非常冗长,且难以实现。
三年后, Fisk 发表的论文 [2] 提供了一种极大简化了的证明,通过简单多边形的三角剖分 及三染色优美地解决了这个问题。 Fisk 的证明虽然优美,但是依赖于简单多边形 三角剖分的存在性及简单多边形无洞的事实。
如何将一个简单多边形进行三角剖 分?Chazelle [3] 在 1990 年证明,简单多边形可以在线性时间内得到三角剖分,但 是这个算法太过复杂,几乎没有人去实现。更常见的做法 [4] 是采用两步:(1) 将 简单多边形分解为若干个单调多边形;(2) 对每个单调多边形进行三角剖分。本次 project,我们将采用 [4] 中的两步方法,也即课上教的方法,对简单多边形进行三 角剖分,具体包括
- 简单多边形分解成单调多边形;
- 单调多边形的三角剖分;
- 利用 Fisk 方法进行染色,生成 n3 ⌋ 个哨兵的监视方案;
- 三角剖分测例生成与正确性验证;
- 简单直观易用的图形界面(手动创建多边形、算法流程可视化)。
4.4 Steve Fisk 的证明
Steve Fisk 的证明是如此简短和优雅,以至于它被选为包含在 THE BOOK 的证明中。 [4]证明如下:
首先,对多边形进行三角剖分(不添加额外的顶点),这是可能的,因为在某些经过验证的条件下证明了三角剖分的存在。生成的三角剖分图的顶点可能是三色的。[a] 显然,在三色下,每个三角形都必须具有所有三种颜色。具有任何一种颜色的顶点构成一个有效的保护集,因为多边形的每个三角形都由具有该颜色的顶点保护。由于这三种颜色划分了多边形的 n 个顶点,因此具有最少顶点的颜色定义了一个有效的守卫集,最多n/3警卫。