腾讯音乐笔试0414

news2025/11/1 7:38:36

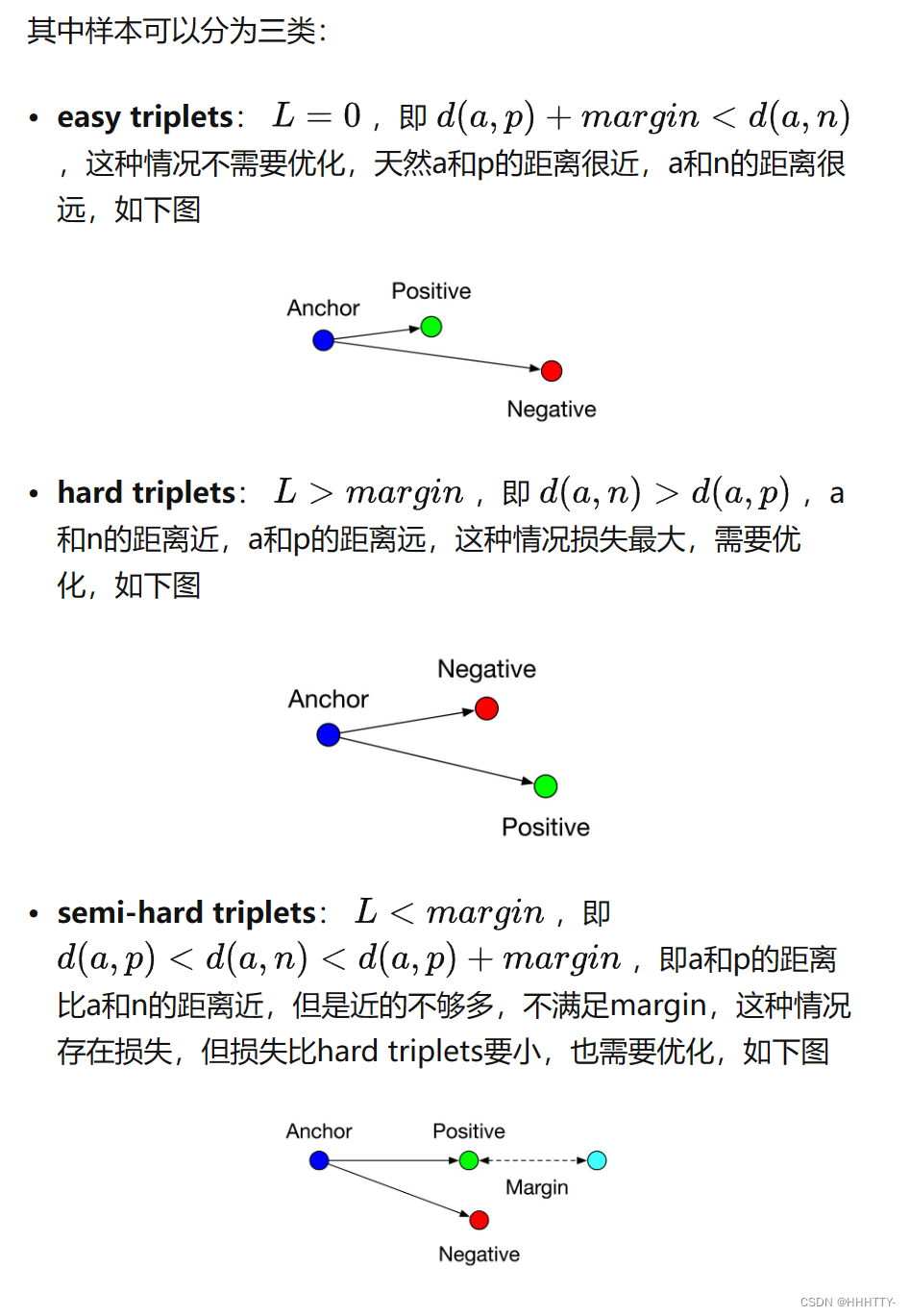
介绍一 Triplet Loss的原理，其中的样本分为哪几类?可以用于哪些场景?

Triplet Loss是一种用于训练神经网络的损失函数，主要用于学习映射函数，将样本映射到低维空间中，使得同一类别的样本距离尽可能近，不同类别的样本距离尽可能远。

在Triplet Loss中，每个样本被分为三类：Anchor，Positive和Negative。其中Anchor表示一个锚点样本，Positive表示和Anchor属于同一类别的样本，Negative表示和Anchor不属于同一类别的样本。

Triplet Loss的原理是，对于一个Anchor样本，选择与其属于同一类别的Positive样本和不属于同一类别的Negative样本，计算Anchor到Positive的距离和Anchor到Negative的距离，使得这两个距离之间的差距大于一定的阈值，从而让模型学习到对同一类别的样本更为相似，对不同类别的样本更为不同的特征表示。

Triplet Loss可以用于许多场景，例如人脸识别、图像检索、推荐系统等。在这些场景中，Triplet Loss可以帮助模型学习到区分不同类别样本的特征，从而提高模型的准确性和鲁棒性。

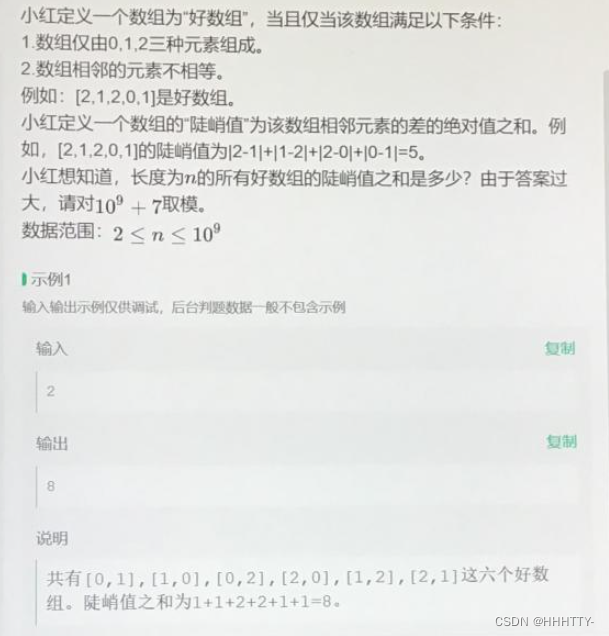
在这里插入图片描述

T1 好数组

在这里插入图片描述

开始认为是一个dp问题，最后变成了求通项公式。。

通项公式为:
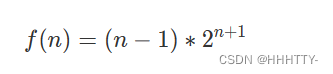
在这里插入图片描述

T1:数学递推递推后的式子为fn=(n-1)*2^(n+1) 用快速幂计算即可

通过快速幂求解即可，注意类型为long long:

#define MOD 1000000007
typedef long long ll;

class Solution {
public:
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     *
     * @param n int整型
     * @return int整型
     */
    ll fastpow(ll n, ll val){
        if(n == 1) return val;
        if(n == 0) return 1;

        ll x = fastpow(n/2, val);
        return n % 2 ? ((x*x) % MOD*val) % MOD : (x*x) % MOD;
    }

    int fun(int n) {
        return (ll)((n-1)*fastpow(n+1, 2)) % MOD;
    }
};

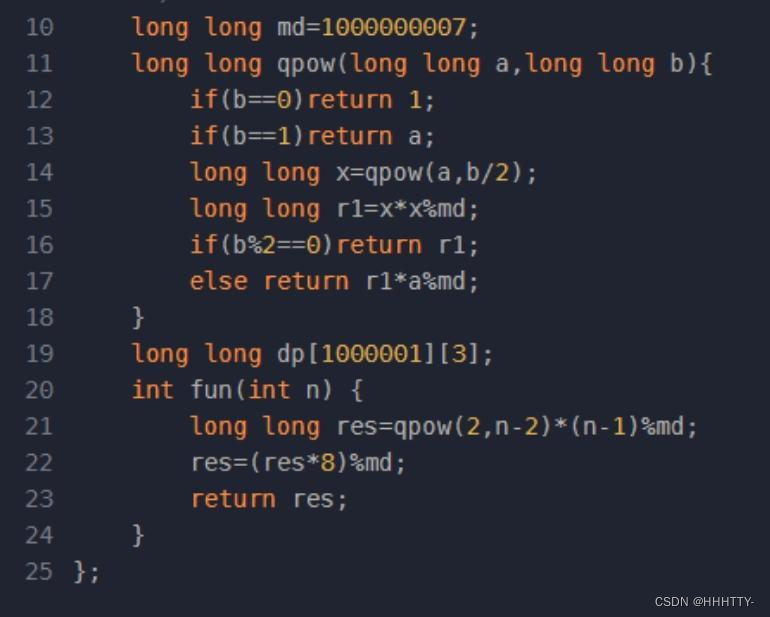
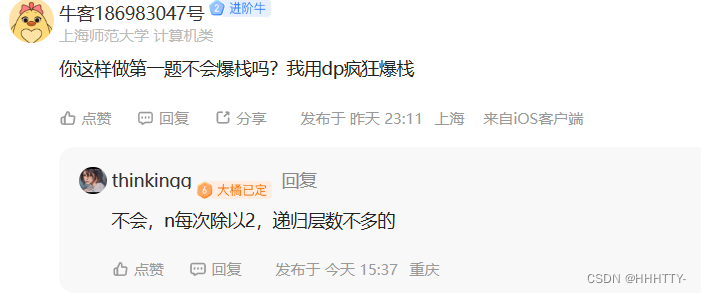
在这里插入图片描述

为啥我第一题用了快速幂也不可以呀？
应该是long long的问题 int定义的话不行，第一题测试样例很恶心

第一题怎么退出来的公式啊
手玩，等比数列求和，感觉像是高中数学题

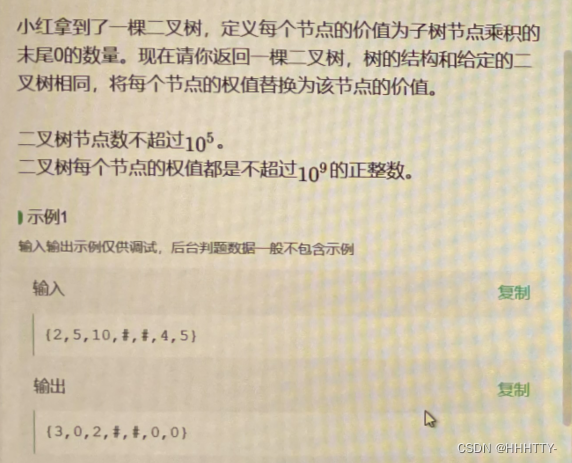
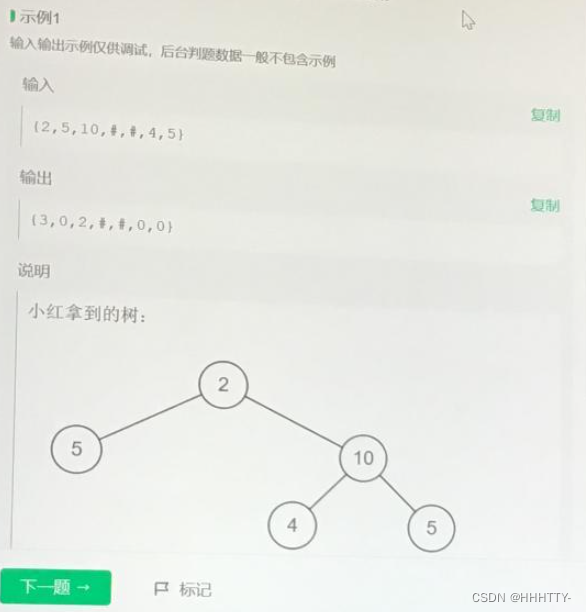
在这里插入图片描述

T2 二叉树

在这里插入图片描述

小红拿到了一棵叉树，定义每个节点的价值为子树节点乘积的末尾0的数量。

现在请你返回一棵叉树，树的结构和给定的二叉树相同，将每个节点的权值替换为该节点的价值。

二叉树节点数不超过 $10^5$
二叉树每个节点的权值都是不超过 $10^9$ 的正整数。

在这里插入图片描述

T2:
简单DFS

题目的意思是

求每个节点的子树所有元素乘积中0的个数(10->1 100->2 500->2)
自定向下DFS统计每个元素%2的数量a和%5的数量b即可
求一个和乘积中0的个数转换为min(a,b)

在这里插入图片描述

class Solution {
public:
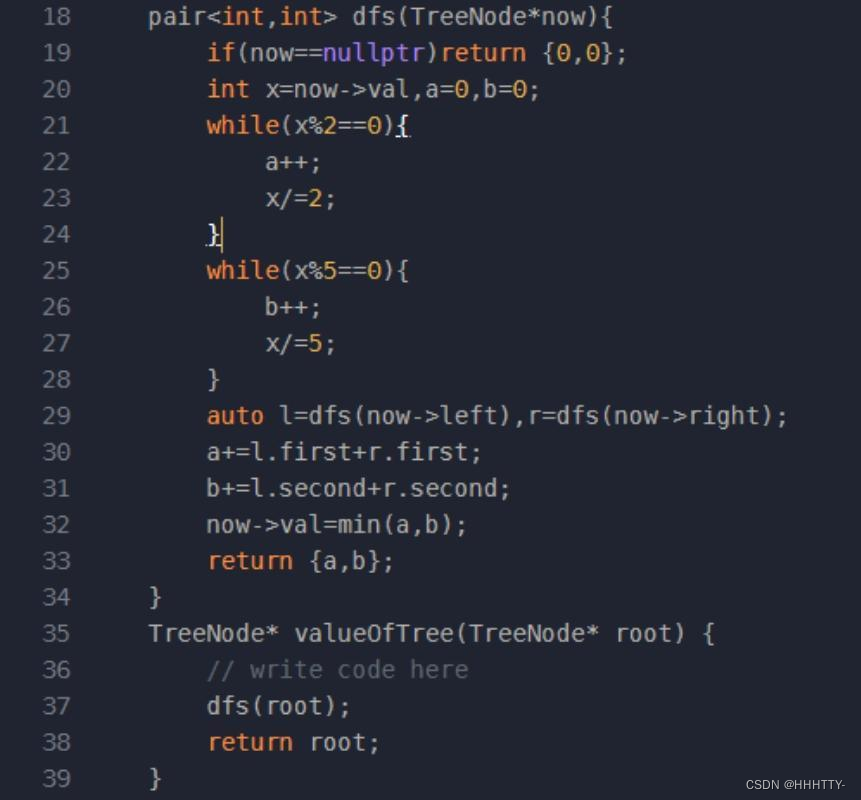
   TreeNode* valueOfTree(TreeNode* root) {
       // write code here
       dfs(root);
       return root;
   }

   pair<int,int> dfs(TreeNode* node){
       if(node == nullptr){
           return {0, 0};
       }
       auto l = dfs(node->left);
       auto r = dfs(node->right);
       auto cur = cal(node->val);
       auto n2 = cur.first + l.first + r.first;
       auto n5 = cur.second + l.second + r.second;
       node->val = min(n2, n5);
       return {n2, n5};
   }

   //末尾0的数量与因子2和5的数量有关系
   pair<int,int> cal(int num){
       int n2 = 0, n5 = 0;
       while(num%2 == 0){
           num /= 2;
           n2 += 1;
       }
       while(num%5 == 0){
           num /= 5;
           n5 += 1;
       }
       return {n2,n5};
   }
};

在这里插入图片描述

T3 构造一个大小是 n*(n+ 1)/2的数组

给定正整数n,小红希望你构造一个大小是 n*(n+ 1)/2的数组，
有1个1, 2个2, …n个n,且任意两个相邻元素都不相等。你能帮帮她吗?

答案不唯一，
有多解时输出任意合法解均可通过。
数据范围: 1 < n< 500

示例1

输入
3
输出
[3,2,3,2,3,1]

在这里插入图片描述

T3:贪心

优先存放剩余最多的数(用一个大根堆记录每个数字剩余的次数如果堆顶元素和当前元素不相同

则直接push堆顶元素堆顶元素的数量-1

如果相同 pop一下在push堆顶元素

再push一下之前pop的元素即可)

第三题很简单，就321 32，4321 432 43，。。。不用贪心，两行代码解决了

就两个for循环

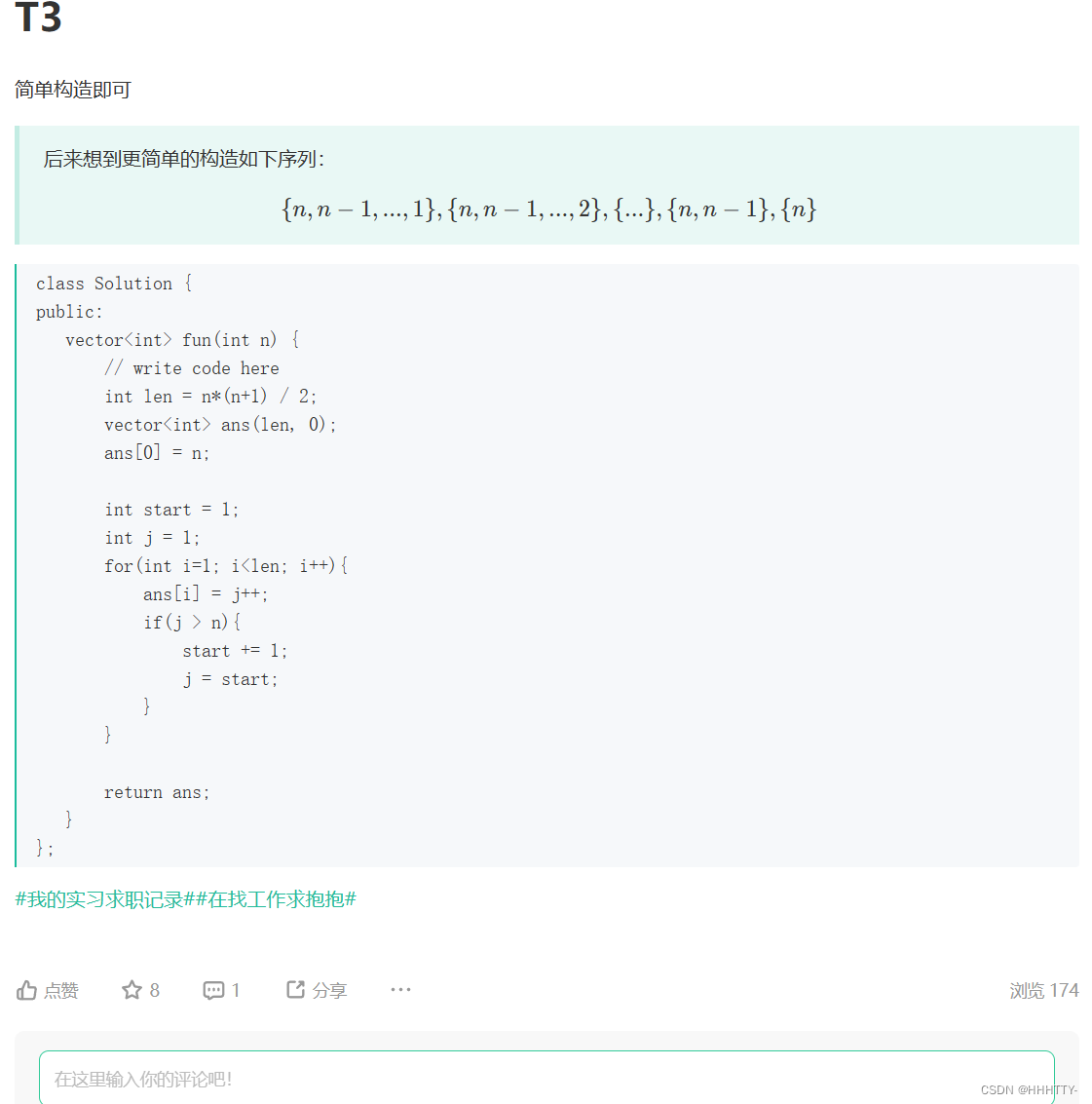
在这里插入图片描述

class Solution {
public:
   vector<int> fun(int n) {
       // write code here
       int len = n*(n+1) / 2;
       vector<int> ans(len, 0);
       ans[0] = n;

       int start = 1;
       int j = 1;
       for(int i=1; i<len; i++){
           ans[i] = j++;
           if(j > n){
               start += 1;
               j = start;
           }
       }

       return ans;
   }
};

def construct_array(n):
    arr = [0] * (n * (n + 1) // 2)
    index = 0
    for i in range(1, n+1):
        count = i
        while count > 0:
            arr[index] = i
            index += 2*i if count == i else 1
            count -= 1
    return arr

函数construct_array(n)会返回一个符合要求的长度为n*(n+1)/2的数组。该算法的思路是对于每个数字i，将它重复i次放入数组中，但是每隔i个位置跳过一个位置，这样可以保证相邻元素不相等。

例如，当n=3时，构造的数组应该是[1,2,1,3,2,3]。在该算法中，我们首先初始化一个长度为n*(n+1)/2的数组，然后从1到n枚举每个数字i。对于每个数字i，我们将其重复i次，然后按照上述规则放入数组中。具体地，我们需要维护一个指针index，它表示当前应该将数字i插入的位置。然后我们从i开始，将i插入到数组的第index个位置。接着，如果我们还有剩余的i需要插入，就将index跳过2*i个位置，因为这样才能保证相邻元素不相等。如果我们只剩下1个i需要插入，就将index跳过1个位置。

最后，返回构造好的数组即可。

在这里插入图片描述