一、哈希表

哈希表，又被称之为散列表（Hash Table），它是一种数据结构。在Java中：JDK1.7版本之前，哈希表的底层实现是数组+链表，即数据结构中所说的拉链法；而在JDK1.8版本之后，哈希表的底层实现则是数组+链表+红黑树。而无论是JDK1.8之前还是JDK1.8之后，哈希表数组的初始值均为16，默认加载因子为0.75。

那什么是加载因子呢？例如数组的长度为16，存入数组的数据元素个数为4个，那么此数组的加载因子为4/16=0.25，而哈希表中规定的加载因子是为扩容作准备的。当哈希表的数组中存入数据达到16*0.75=12个时，数组会自动扩容，扩容至原来数组长度的两倍，即16*2=32，之后同样的若哈希表的数组中存入数据达到32*0.75=24个时，数组会自动扩容至原来数组长度的两倍，即32*2=64，之后以此类推。

那么哈希表具体是怎么实现的呢？接下来我们将结合例图来详细讲解。

1.1 JDK1.7版本之前哈希表（数组+链表，头插法）

当我们创建了一个HashSet或者HashMap对象时，系统会自动为我们创建一个初始值为16，加载因子为0.75的哈希表，如下图所示：

---

当我们向集合中添加一个数据时，系统会根据特定的散列函数来计算此数据元素将要存储在数组的哪一位置。例如若我们要添加一个"aa"，经过系统散列函数计算后，得到散列值为4，即系统将会把"aa"存入到数组下标为4的位置，而此时数组为空，可以直接存入数据，如下图所示：

---

之后我们再次添加一个元素"aaa"，若此时它的散列值也为4，系统判断出数组下标为4的位置已经存在元素，则系统将会采用头插法（旧元素插在新元素之后）将"aaa"插入数组，如下图所示：

---

之后我们再次添加一个元素"bbb"，若此时它的散列值也为4，系统判断出数组下标为4的位置已经存在元素，则系统将会采用头插法（旧元素插在新元素之后）将"bbb"插入数组，如下图所示：

---

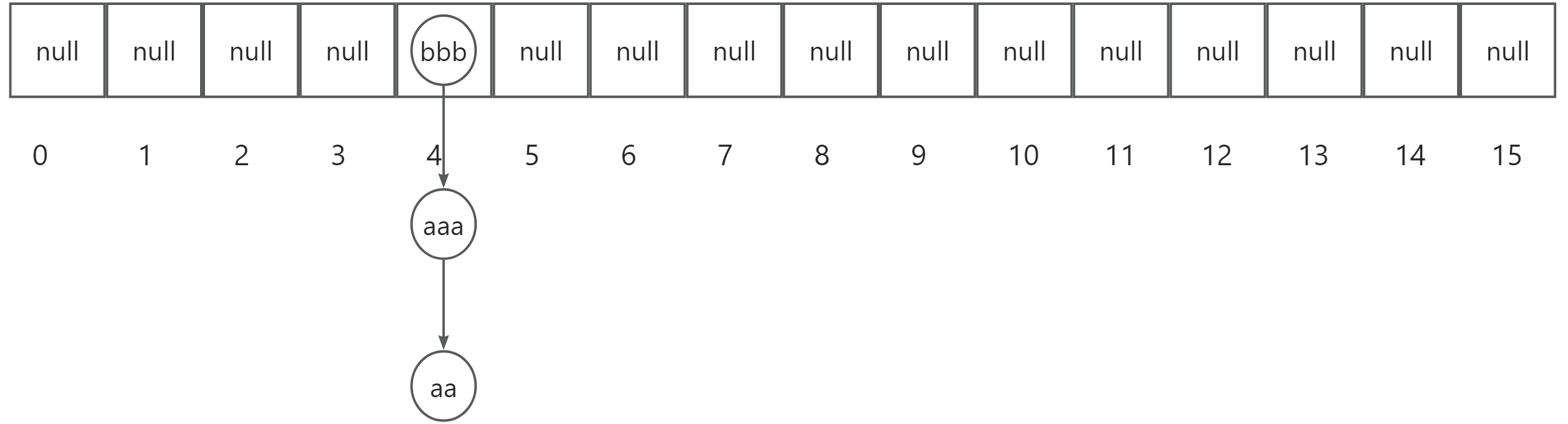
之后我们再次添加一个元素"b"，若此时它的散列值为6，系统判断出数组下标为6的位置为空，则系统将会直接存入数据，如下图所示：

---

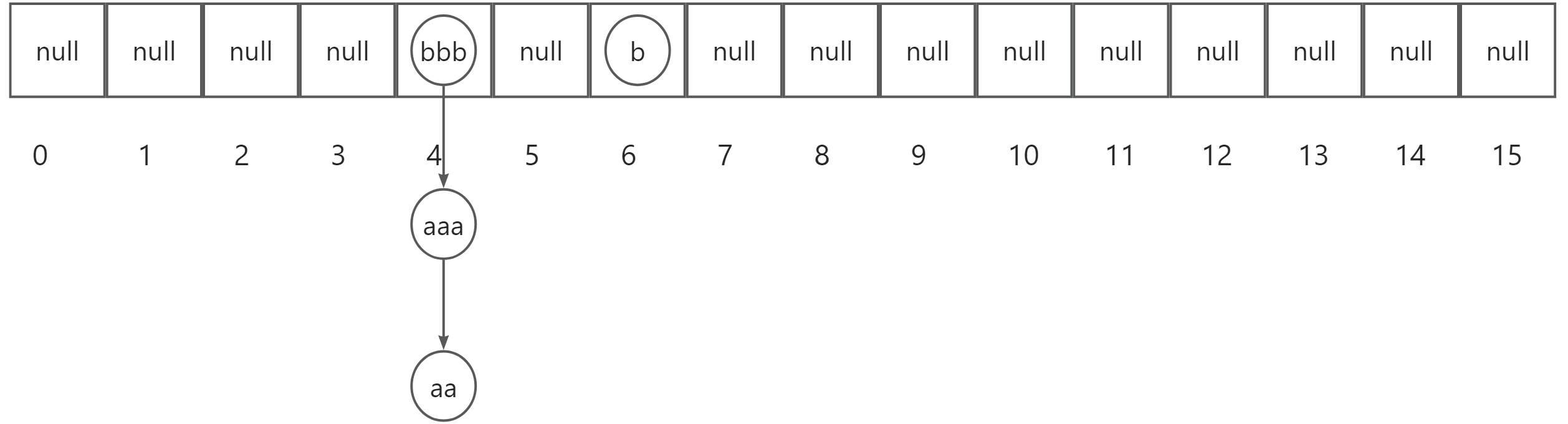
之后我们依次添加元素，直到数组的加载因子为0.75，即16*0.75=12，（注意：加载因子的计算我们只看数组上的元素，而不考虑链接的元素）如下图所示：

---

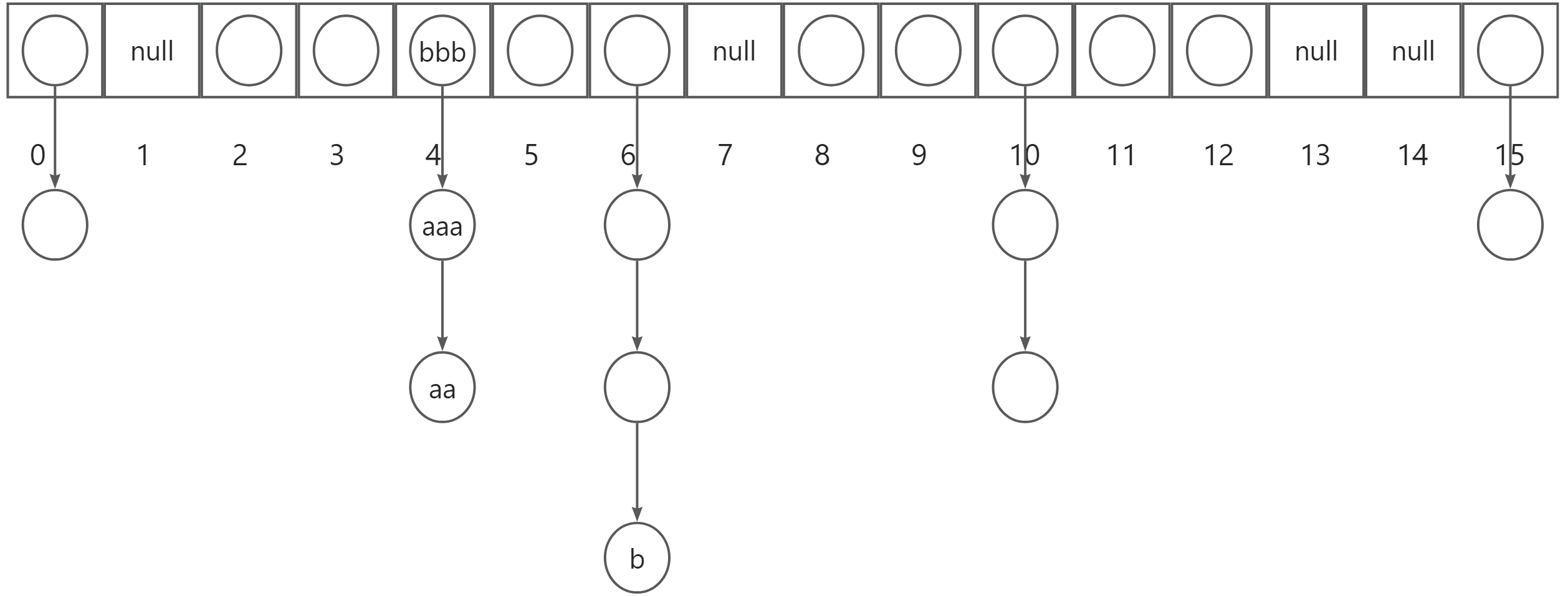
那么数组将会自动扩容至原来容量的2倍，之后以此类推。如下图所示：

---

1.2 JDK1.8版本之后哈希表（数组+链表+红黑树，尾插法）

当我们创建了一个HashSet或者HashMap对象时，系统会自动为我们创建一个初始值为16，加载因子为0.75的哈希表，如下图所示：

---

当我们向集合中添加一个数据时，系统会根据特定的散列函数来计算此数据元素将要存储在数组的哪一位置。例如若我们要添加一个"aa"，经过系统散列函数计算后，得到散列值为4，即系统将会把"aa"存入到数组下标为4的位置，而此时数组为空，可以直接存入数据，如下图所示：

---

之后我们再次添加一个元素"aaa"，若此时它的散列值也为4，系统判断出数组下标为4的位置已经存在元素，则系统将会采用尾插法（新元素插在旧元素之后）将"aaa"插入数组，如下图所示：

---

之后我们再次添加一个元素"bbb"，若此时它的散列值也为4，系统判断出数组下标为4的位置已经存在元素，则系统将会采用尾插法（新元素插在旧元素之后）将"bbb"插入数组，如下图所示：

---

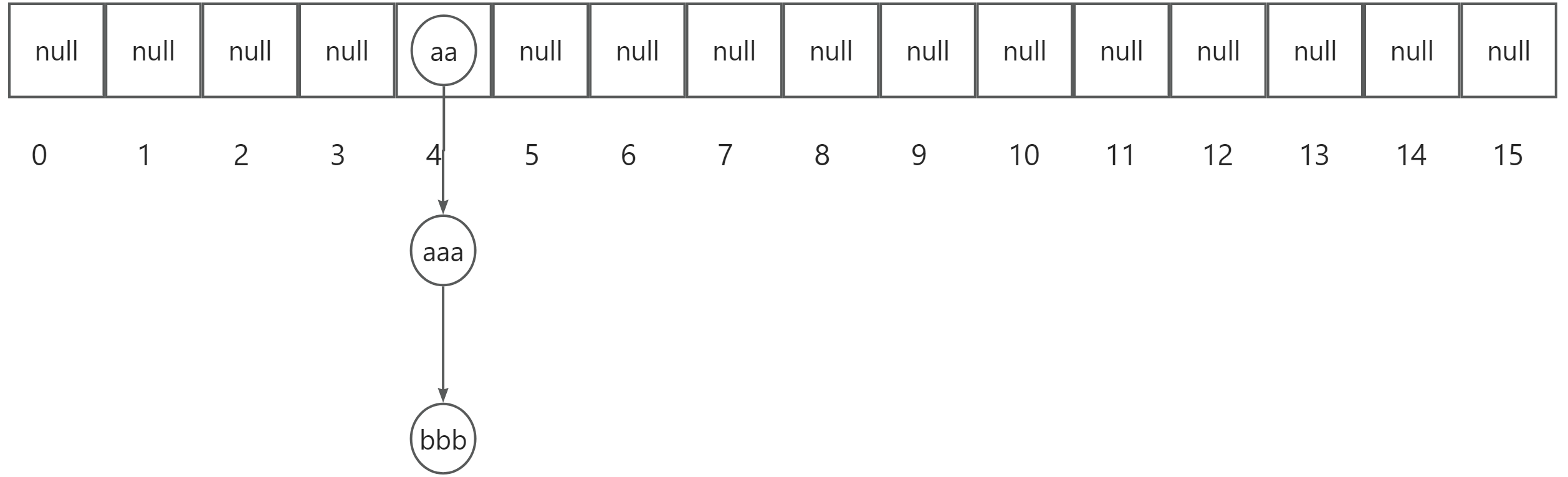
之后我们再次添加一个元素"b"，若此时它的散列值为6，系统判断出数组下标为6的位置为空，则系统将会直接存入数据，如下图所示：

---

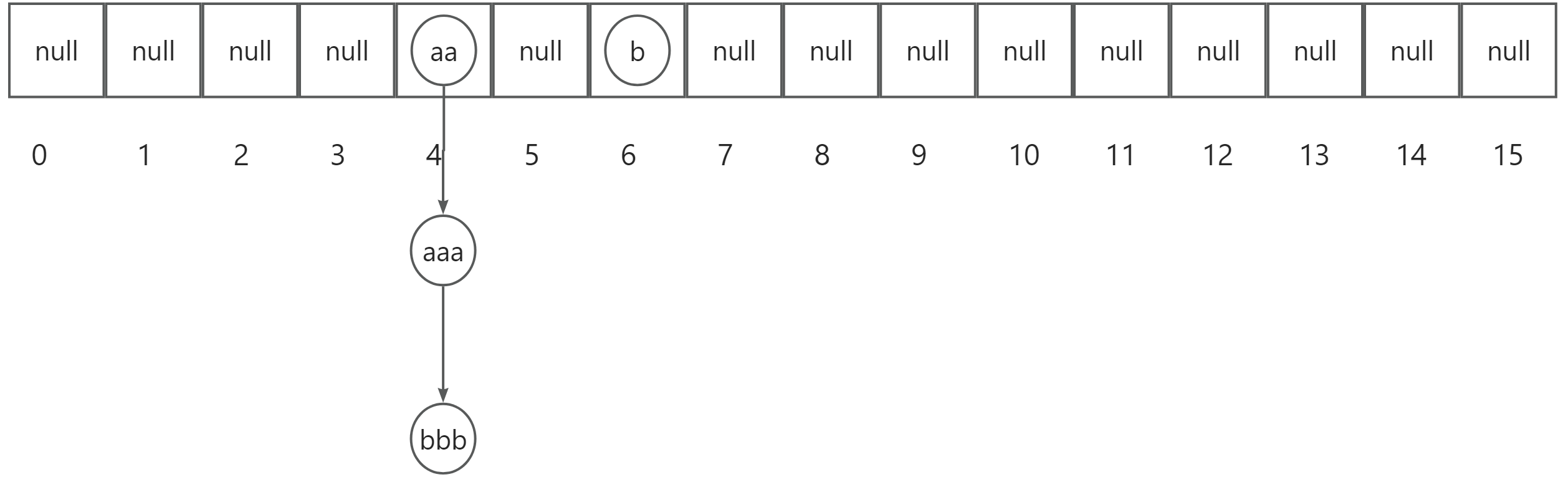
之后我们依次添加元素，直到数组的加载因子为0.75，即16*0.75=12，（注意：加载因子的计算我们只看数组上的元素，而不考虑链接的元素）如下图所示：

---

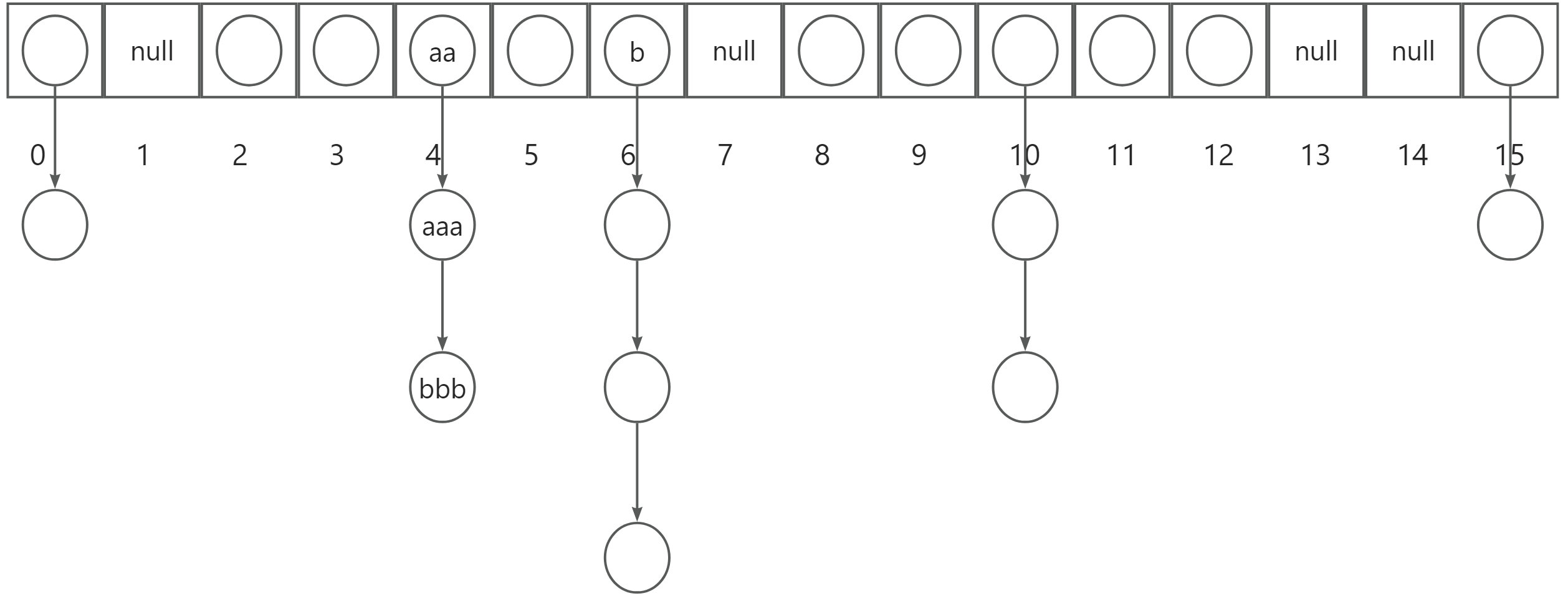
那么数组将会自动扩容至原来容量的2倍，之后以此类推。如下图所示：

---

二、红黑树

那么红黑树又是什么呢？

红黑树是一种自平衡（根据红黑规则定义的平衡，它和平衡二叉树定义的平衡不一样）的二叉查找树，它是一种数据结构，我们可以将它看作是一种特殊的二叉查找树，它的每一个节点都有存储位来表示结点的颜色，每个节点要么是黑色，要么是红色。

红黑规则：
1、每一个节点或是红色的，或是黑色的。
2、根节点必须是黑色的。
3、所有的叶子节点（叶子节点为空，我们可以理解为它们不是真实的节点）均是黑色的。
4、如果一个节点是红色的，那么它的父节点和孩子节点均不能为红色（即红色节点不能直接相连）
5、对于每一个节点，它到后代任意叶子节点的简单路径上，均包含相同数量的黑色节点。

那么红黑树具体是怎么实现的呢？接下来我们将结合例图来详细讲解。

假设我们当前有三个节点，分别为2，13，1并且节点颜色均为红色（注意，在创建红黑树时，节点颜色均为红色或黑色），如下图所示：

---

我们拿取节点2作为根节点，由于根节点必须为黑色，因此节点2需要变为黑色，之后为它添加两个叶子节点（叶子节点必须是黑色的），如下图所示：

---

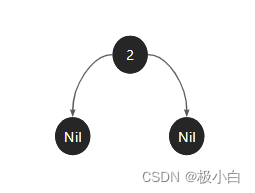
之后我们向红黑树插入节点13，由于13>2，因此需要将节点13插入节点2的右子树，之后为它们配齐叶子节点，我们发现它满足红黑规则，如下图所示：

首先来看节点2，它作为根节点为黑色，并且它到后代任意叶子节点的简单路径上均只包含1个黑色节点。

之后我们来看节点13，它为红色节点，未与其他红色节点直接相连，并且它到后代任意叶子节点的简单路径上均只包含1个黑色节点。因此它满足红黑规则。

---

之后我们向红黑树插入节点1，由于1<2，因此需要将节点1插入节点2的左子树，之后为它们配齐叶子节点，同样我们发现它满足红黑规则，如下图所示：

首先来看节点2，它作为根节点为黑色，并且它到后代任意叶子节点的简单路径上均只包含1个黑色节点。

之后我们来看节点13，它为红色节点，未与其他红色节点直接相连，并且它到后代任意叶子节点的简单路径上均只包含1个黑色节点。

最后我们来看节点1，它为红色节点，未与其他红色节点直接相连，并且它到后代任意叶子节点的简单路径上均只包含1个黑色节点。

---

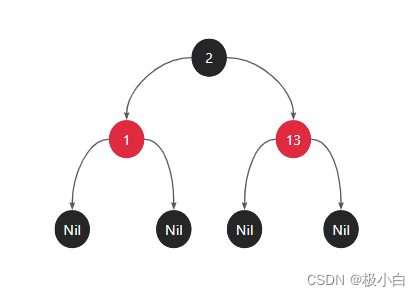
那如果我们再插入一个节点0，会发生什么呢？由于0<2，因此需要将节点0插入到节点2的左子树，由于0<1，因此需要将节点0插入到节点1的左子树。我们根据图解查看它会发生什么！！！

---

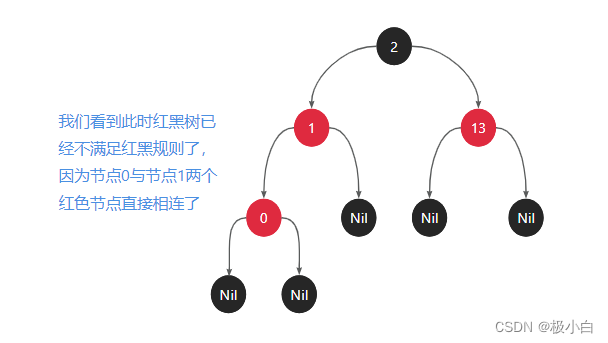
2.1 使红黑树再次满足红黑规则

它共有两种方式：

2.1.1 使红黑树满足红黑规则方法一

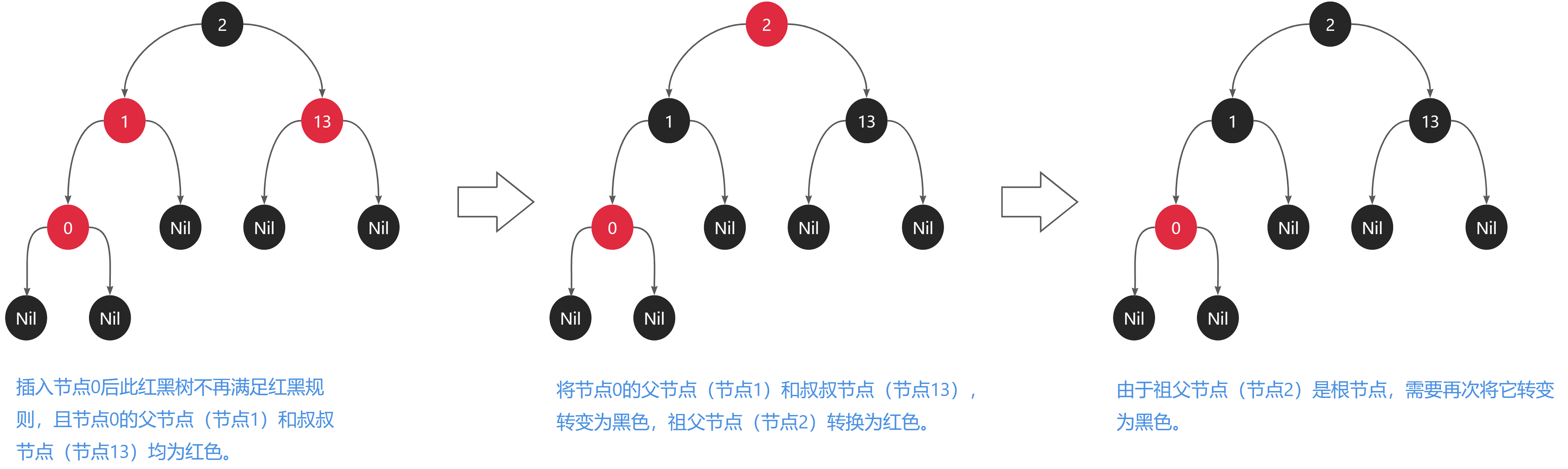
添加节点时，若节点的父亲节点和叔叔节点均为红色，则需要将父亲节点和叔叔节点均转变为黑色，并将祖父节点转换为红色，若祖父节点为根节点则需要再将其转变为黑色。

我们所写的例子即为此种情况，那么我们就需要将节点0的父节点（节点1）和叔叔节点（节点13）均转变为黑色，并将祖父节点（节点2）转变为红色，因为节点2为根节点，因此我们需要再次将其转变为黑色。如下图所示：

---

2.1.2 使红黑树满足红黑规则方法二

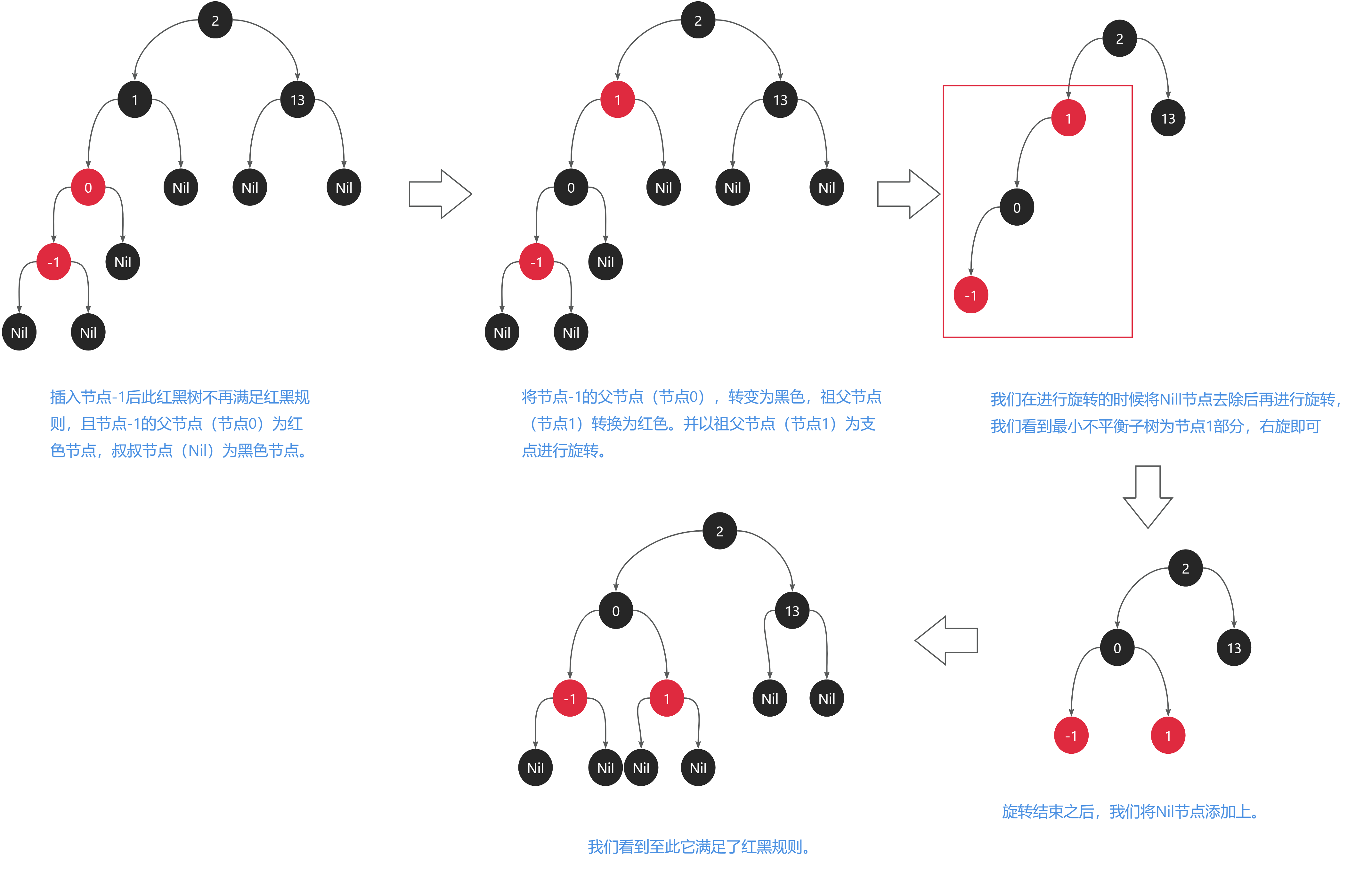
添加节点时，若节点的父亲节点为红色，叔叔节点为黑色，则需要将父亲节点转变为黑色，将祖父节点转换为红色，并以祖父节点为支点进行旋转。

之后我们再次添加一个节点-1，由于-1<2，因此需要将节点-1插入到节点2的左子树，由于-1<1，因此需要将节点-1插入到节点1的左子树，由于-1<0，需要将节点-1插入到节点0的左子树。如下图所示：

---

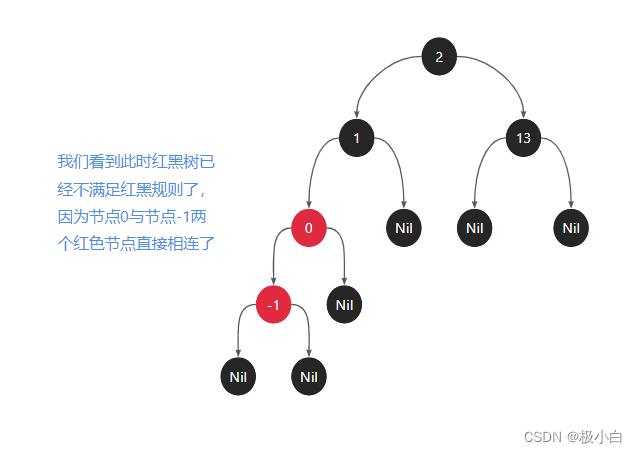
我们看到节点-1的父节点（节点0）为红色节点，叔叔节点（Nil）为黑色节点，此时需要将其父节点（节点0）转换为黑色，祖父节点（节点1）转换为红色，并以祖父节点（节点1）为支点进行旋转。如下图所示：

---

三、JDK1.7与JDK1.8哈希表结构不同原因

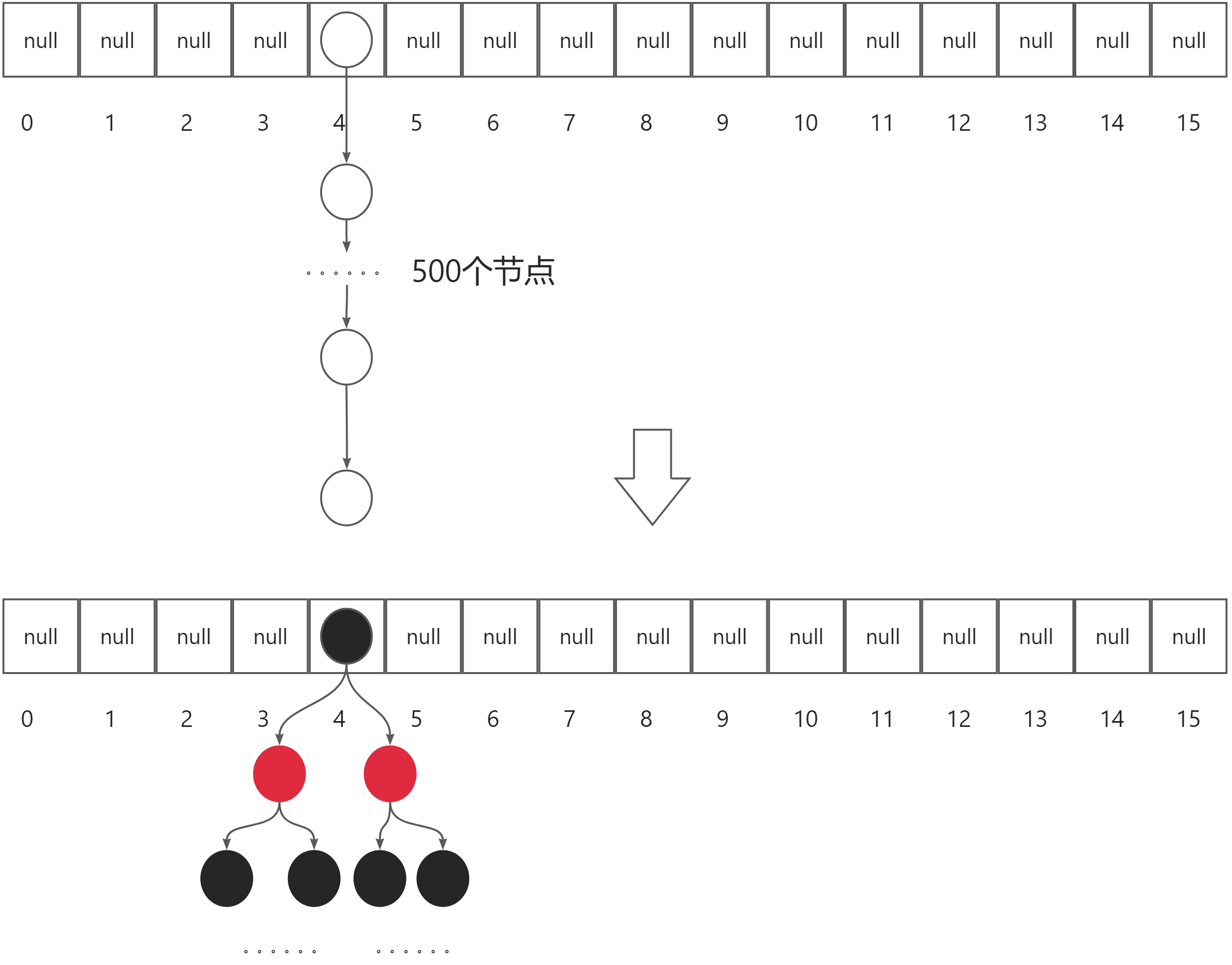
那为什么JDK1.8之后我们要再添加红黑树结构呢？我们一起来看一个例子：若此时数组的某一个链表长度为500个节点（极端例子，现实中不会出现），那么我们在查询某一个元素时，有时甚至需要查询500次才能查到我们想要查询的数据，但若是我们将链表转化为红黑树后，查询效率将会大大提高！！！因此我们就规定当数组元素达到64，链表长度达到8时，链表会自动转换为红黑树结构。

---

OK！！！至此哈希表我们就介绍完毕！！！