文章目录
- #搜索二叉树
- 1. 搜索二叉树特点
- 2. 操作分析
- 2.0 结点结构
- 2.1 插入
- 2.2 升序查看
- 2.3 查找
- 2.4 删除
- 2.5 前序拷贝构造
- 3. 完整代码
- 4. 时间复杂度分析
- 5. 简单应用
- 5.1 字典搜索
- 5.2 统计次数
#搜索二叉树
1. 搜索二叉树特点
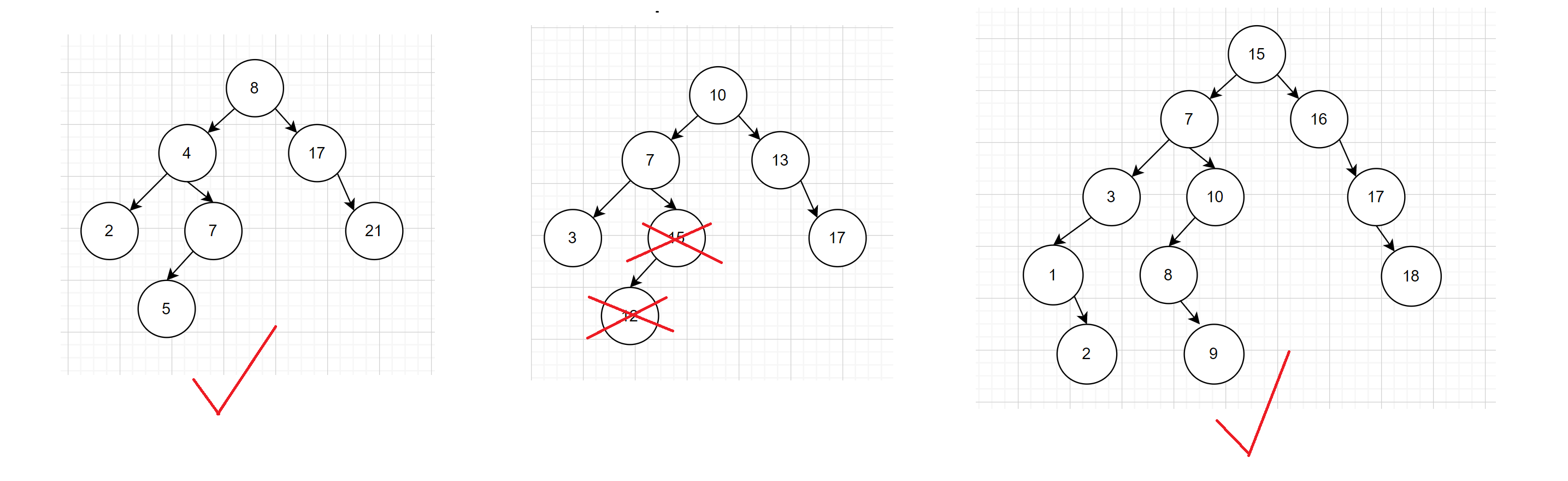
- 若它的左子树不为空,则左子树上所有节点的值都小于根节点的值
- 若它的右子树不为空,则右子树上所有节点的值都大于根节点的值
- 每个结点的左右子树也分别为二叉搜索树
见一见:
2. 操作分析
2.0 结点结构
template <class KEY>
struct node
{
node<KEY>* _left;
node<KEY>* _right;
KEY _key;
node(const KEY& key)
:_left(nullptr)
, _right(nullptr)
, _key(key)
{}
};
//声明:
//typedef struct node<KEY> node;
//typedef node* node_pointer;
2.1 插入
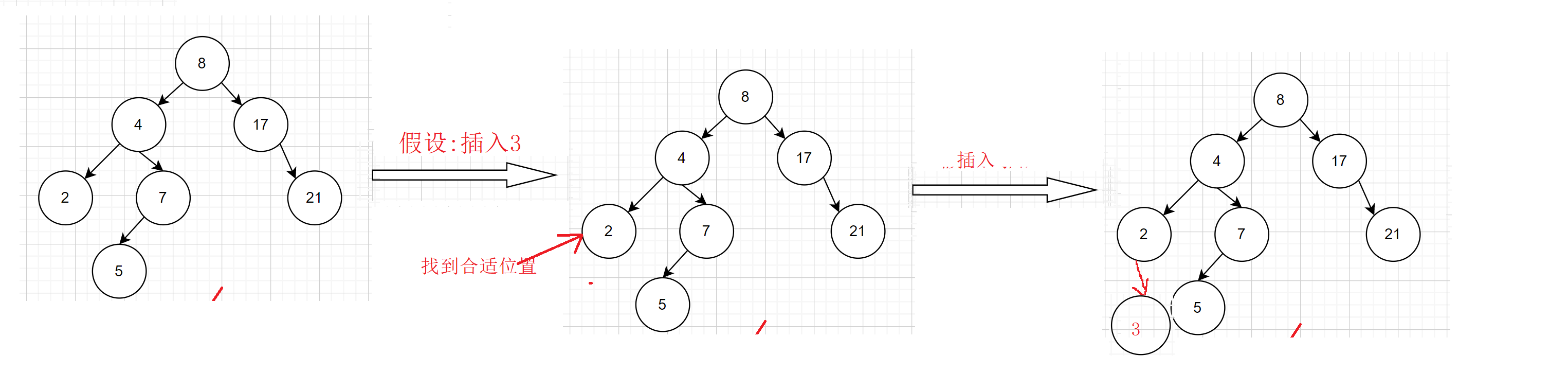
- 非递归插入
bool insert_nonRecurse(const KEY& key)
{
//a. 树为空
if (_root == nullptr)
{
_root = new node(key);
return true;
}
//b. 树不为空,按性质插入
node_pointer cur = _root;
node_pointer parent = nullptr;
//b.1 找合适位置
while (cur != nullptr)
{
if (key > cur->_key) //b.1.1 key > cur->_key --> 右遍历
{
parent = cur;
cur = cur->_right;
}
else if (key < cur->_key) //b.1.2 key < cur->_key --> 左遍历
{
parent = cur;
cur = cur->_left;
}
else //b.1.3 相等 --> false
{
return false;
}
}
//b.2 连接
cur = new node(key);
if (key > cur->_key)
{
parent->right = cur;
}
else
{
parent->_left = cur;
}
return true;
}
- 递归插入
bool insert_recurse(node_pointer& root, const KEY& key)
{
//a. 树为空
if (root == nullptr)
{
root = new node(key);
return true;
}
//b. 树不为空
if (key > root->_key) //右遍历
{
return insert_recurse(root->_right, key);
}
else if (key < root->_key) //左遍历
{
return insert_recurse(root->_left, key);
}
else //相等 --> false
{
return false;
}
}
- node_pointer& 理解

2.2 升序查看
void inOrder(node_pointer root)
{
if (root == nullptr)
return;
_inOrder(root->_left);
cout << root->_key << " ";
_inOrder(root->_right);
}
2.3 查找
bool find(const KEY& key)
{
node_pointer cur = _root;
while (cur != nullptr)
{
if (key > cur->_key) //右遍历
{
cur = cur->_right;
}
else if (key < cur->_key) //左遍历
{
cur = cur->_left;
}
else
{
return true;
}
}
return false;
}
2.4 删除
- 非递归删除
- 删除左右子树都为空的节点(叶子节点)
- 找到节点
- 判断是否为头节点(直接删除,头节点置空)
- 删除节点
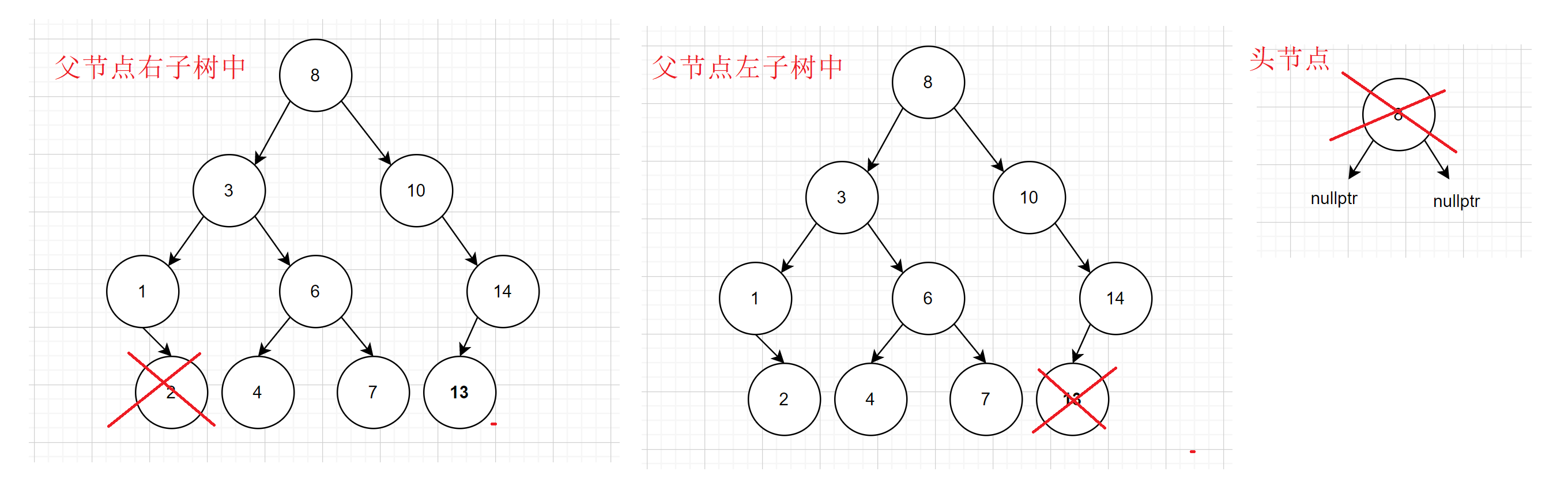
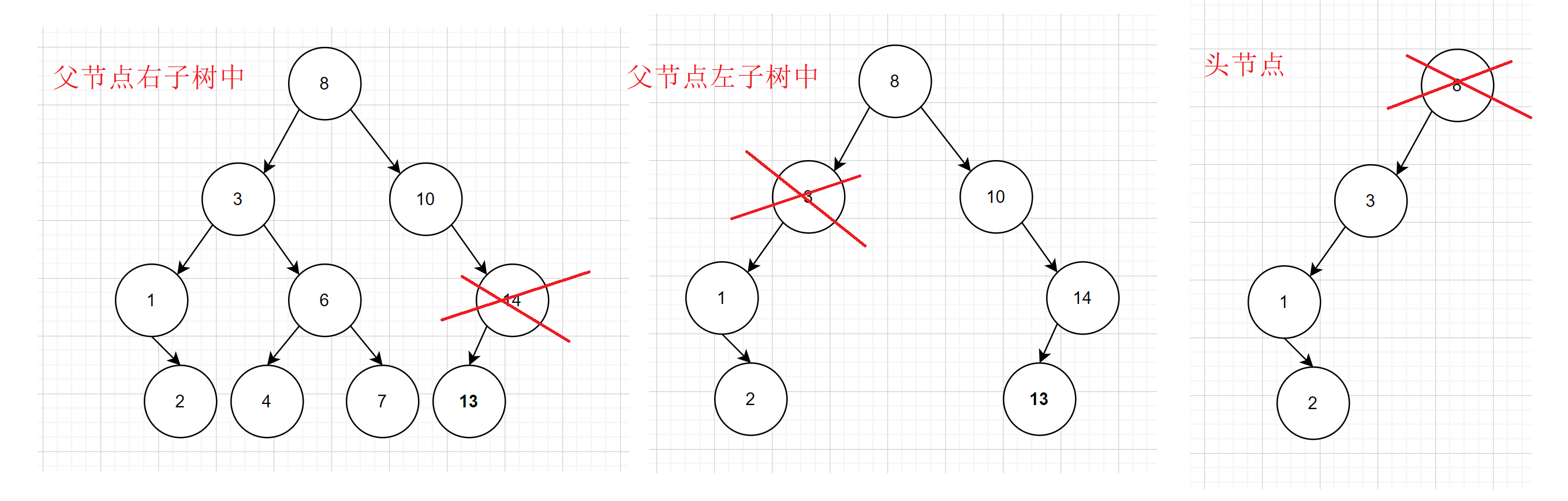
- 删除左子树为空,右子树不为空
- 找到节点
- 判断被删除节点是否为头节点(单独处理,头节点指向头节点右子树)
- 判断被删除节点在其父节点左子树还是右子树中(连接问题要分支考虑)
- 被删除节点在父节点左子树中(父节点左子树指向被删除节点右子树)
- 被删除节点在父节点右子树中(父节点右子树指向被删除节点右子树)
- 删除节点
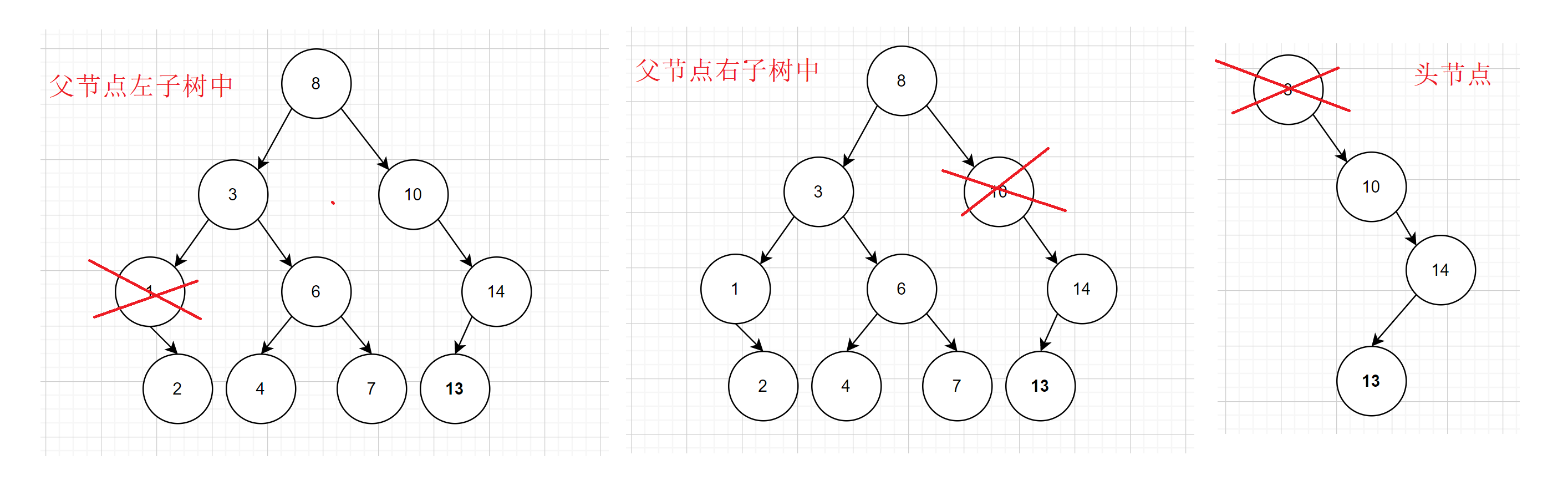
- 删除左子树不为空,右子树为空
- 找到节点
- 判断被删除节点是否为头节点(单独处理,头节点指向头节点左子树)
- 判断被删除节点在其父节点左子树还是右子树中(连接问题要分支考虑)
- 被删除节点在父节点左子树中(父节点左子树指向被删除节点左子树)
- 被删除节点在父节点右子树中(父节点右子树指向被删除节点左子树)
- 删除节点
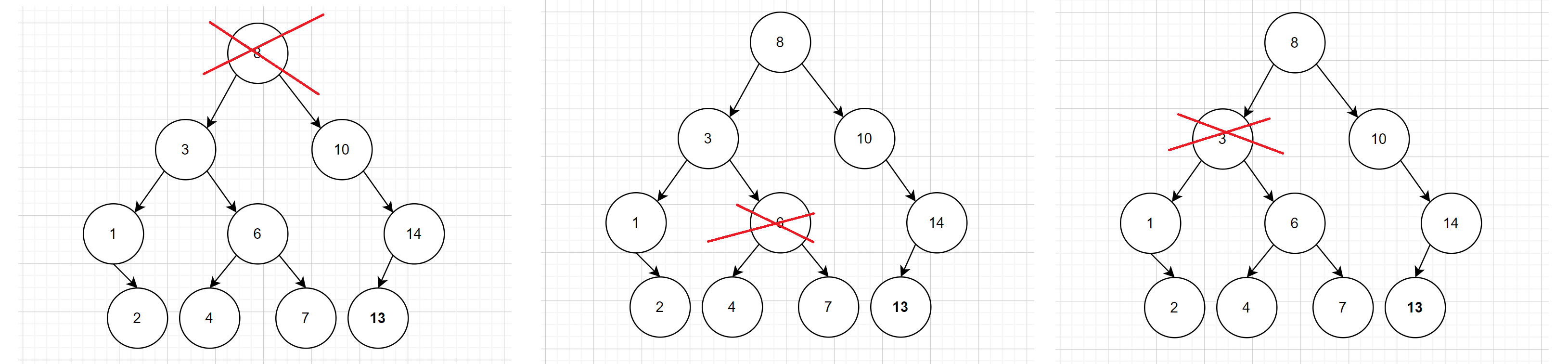
- 删除左右子树都不为空(右子树最小值交换策略)
- 找到节点
- 取被删除节点右子树最小值节点并得到其最小值节点的父节点
- 被删除节点右子树最小值节点和被删除节点值交换(被删除节点变为原来右子树最小值节点位置)
- 其改变后的被删除节点在其父节点左子树还是右子树中(连接问题要分支考虑)
- 改变后的被删除节点在父节点左子树中(父节点左子树指向被删除节点右子树)
- 改变后的被删除节点在父节点右子树中(父节点右子树指向被删除节点右子树)
- 删除改变后的被删除节点
bool erase_nonRecurse(const KEY& key)
{
node_pointer parent = nullptr;
node_pointer cur = _root;
while (cur != nullptr)
{
if (key > cur->_key) //右遍历
{
parent = cur;
cur = cur->_right;
}
else if (key < cur->_key) //左遍历
{
parent = cur;
cur = cur->_left;
}
else //相等 --> 删除
{
/*被删除节点要区分是在其父节点的左子树还是右子树中*/
if (cur->_left == nullptr) //被删节点左子树为空 && 被删节点左右子树都为空
{
if (cur == _root) //头节点处理
{
_root = cur->_right;
}
else
{
if (parent->_left == cur) //被删除节点在父节点左子树
{
parent->_left = cur->_right;
}
else //被删除节点在父节点右子树
{
parent->_right = cur->_right;
}
}
delete cur;
}
else if (cur->_right == nullptr) //被删节点右子树为空 && 被删节点左右子树都为空
{
if (cur == _root) //头节点处理
{
_root = cur->_left;
}
else
{
if (parent->_left == cur) //被删除节点在父节点左子树
{
parent->_left = cur->_left;
}
else //被删除节点在父节点右子树
{
parent->_right = cur->_left;
}
}
delete cur;
}
else //左右子树都不为空 (策略:右子树最小值交换)
{
node_pointer min_right = cur->_right;
node_pointer parent_min_right = cur;
while (min_right->_left) //取右子树最小值节点
{
parent_min_right = min_right;
min_right = min_right->_left;
}
swap(min_right->_key, cur->_key);
//被删除节点父节点和其节点右子树连接(支持原因:右子树最小值只可能拥有右子树不可能拥有左子树)
if (parent_min_right->_left == min_right) //右子树最小值节点(被删除节点)在其父节点左子树
{
parent_min_right->_left = min_right->_right;
}
else //右子树最小值节点在其父节点右子树
{
parent_min_right->_right = min_right->_right;
}
delete min_right;
}
return true;
}
}
return false;
}
- 递归删除
bool _erase_Recurse(node_pointer& root, const KEY& key)
{
if (root == nullptr)
{
return false;
}
if (key > root->_key) //右遍历
{
_erase_Recurse(root->_right, key);
}
else if (key < root->_key) //左遍历
{
_erase_Recurse(root->_left, key);
}
else //相等 --> 删除
{
node_pointer deleted_node = root;
if (root->_left == nullptr) //被删节点左子树为空 && 被删节点左右子树都为空
{
root = root->_right;
}
else if (root->_right == nullptr) //被删节点右子树为空 && 被删节点左右子树都为空
{
root = root->_left;
}
else //左右子树都不为空(策略:右子树最小值和被删节点交换)
{
node_pointer min_right = root->_right;
while (min_right->_left) //取被删节点右子树最小值
{
min_right = min_right->_left;
}
//交换数值
swap(min_right->_key, root->_key);
return _erase_Recurse(root->_right, key); //交换后删除值为min_right节点(右子树遍历)
}
delete deleted_node;
return true;
}
}
- 删除小结
首先考虑被删节点的左右子树都不为空&&被删节点的左子树为空右子树不为空&&被删节点的右子树为空左子树不为空&&被删节点左右子树都不为空四种情况(其中,被删节点的左子树为空右子树不为空&&被删节点的右子树为空左子树不为空包含被删节点的左右子树都不为空的情况)
2.5 前序拷贝构造
binary_search_tree(const binary_search_tree<KEY>& tree)
{
_root = _copy(tree._root);
}
node_pointer _copy(node_pointer root)
{
if (root == nullptr)
{
return nullptr;
}
node_pointer new_node = new node(root->_key);
new_node->_left = _copy(root->_left);
new_node->_right = _copy(root->_right);
return new_node;
}
3. 完整代码
#pragma once
#include <iostream>
#include <algorithm>
#include <utility>
using namespace std;
//模拟实现二叉搜索树
namespace my_tree
{
template <class KEY>
struct node
{
node<KEY>* _left;
node<KEY>* _right;
KEY _key;
node(const KEY& key)
:_left(nullptr)
,_right(nullptr)
,_key(key)
{}
};
template <class KEY>
class binary_search_tree
{
private:
typedef node<KEY> node;
typedef node* node_pointer;
public:
binary_search_tree()
:_root(nullptr)
{}
binary_search_tree(const binary_search_tree<KEY>& tree)
{
_root = _copy(tree._root);
}
binary_search_tree<KEY>& operator=(binary_search_tree<KEY>& tree)
{
_swap(_root, tree._root);
return *this;
}
~binary_search_tree()
{
_destory(_root);
}
void _destory(node_pointer root)
{
if (root == nullptr)
{
return;
}
_destory(root->_left);
_destory(root->_right);
delete root;
root = nullptr;
}
bool insert_nonRecurse(const KEY& key)
{
//a. 树为空
if (_root == nullptr)
{
_root = new node(key);
return true;
}
//b. 树不为空,按性质插入
node_pointer cur = _root;
node_pointer parent = nullptr;
//b.1 找合适位置
while (cur != nullptr)
{
if (key > cur->_key) //b.1.1 key > cur->_key --> 右遍历
{
parent = cur;
cur = cur->_right;
}
else if (key < cur->_key) //b.1.2 key < cur->_key --> 左遍历
{
parent = cur;
cur = cur->_left;
}
else //b.1.3 相等 --> false
{
return false;
}
}
//b.2 连接
cur = new node(key);
if (key > parent->_key) //b.2.1 key > parent_key --> 右连接
{
parent->_right = cur;
}
else //b.2.2 key < parent_key --> 左连接
{
parent->_left = cur;
}
return true;
}
bool insert_recurse(const KEY& key)
{
return _insert_recurse(_root, key);
}
bool find(const KEY& key)
{
node_pointer cur = _root;
while (cur != nullptr)
{
if (key > cur->_key)
{
cur = cur->_right;
}
else if (key < cur->_key)
{
cur = cur->_left;
}
else
{
return true;
}
}
return false;
}
bool erase_nonRecurse(const KEY& key)
{
node_pointer parent = nullptr;
node_pointer cur = _root;
while (cur != nullptr)
{
if (key > cur->_key) //右遍历
{
parent = cur;
cur = cur->_right;
}
else if (key < cur->_key) //左遍历
{
parent = cur;
cur = cur->_left;
}
else //相等 --> 删除
{
/*被删除节点要区分是在其父节点的左子树还是右子树中*/
if (cur->_left == nullptr) //左子树为空 && 左右子树都为空
{
if (cur == _root) //头节点处理
{
_root = cur->_right;
}
else
{
if (parent->_left == cur) //被删除节点在父节点左子树
{
parent->_left = cur->_right;
}
else //被删除节点在父节点右子树
{
parent->_right = cur->_right;
}
}
delete cur;
}
else if (cur->_right == nullptr) //右子树为空 && 左右子树都为空
{
if (cur == _root) //头节点处理
{
_root = cur->_left;
}
else
{
if (parent->_left == cur) //被删除节点在父节点左子树
{
parent->_left = cur->_left;
}
else //被删除节点在父节点右子树
{
parent->_right = cur->_left;
}
}
delete cur;
}
else //左右子树都不为空 (策略:右子树最小值交换)
{
node_pointer min_right = cur->_right;
node_pointer parent_min_right = cur;
while (min_right->_left) //取右子树最小值节点
{
parent_min_right = min_right;
min_right = min_right->_left;
}
swap(min_right->_key, cur->_key);
//被删除节点父节点和其节点右子树连接(支持原因:右子树最小值只可能拥有右子树不可能拥有左子树)
if (parent_min_right->_left == min_right) //右子树最小值节点(被删除节点)在其父节点左子树
{
parent_min_right->_left = min_right->_right;
}
else //右子树最小值节点在其父节点右子树
{
parent_min_right->_right = min_right->_right;
}
delete min_right;
}
return true;
}
}
return false;
}
bool erase_Recurse(const KEY& key)
{
return _erase_Recurse(_root, key);
}
void inOrder()
{
_inOrder(_root);
cout << endl;
}
private:
void _inOrder(node_pointer root)
{
if (root == nullptr)
return;
_inOrder(root->_left);
cout << root->_key << " ";
_inOrder(root->_right);
}
bool _insert_recurse(node_pointer& root, const KEY& key)
{
//a. 树为空
if (root == nullptr)
{
root = new node(key);
return true;
}
//b. 树不为空
if (key > root->_key) //右遍历
{
return _insert_recurse(root->_right, key);
}
else if (key < root->_key) //左遍历
{
return _insert_recurse(root->_left, key);
}
else //相等 --> false
{
return false;
}
}
bool _erase_Recurse(node_pointer& root, const KEY& key)
{
if (root == nullptr)
{
return false;
}
if (key > root->_key) //右遍历
{
_erase_Recurse(root->_right, key);
}
else if (key < root->_key) //左遍历
{
_erase_Recurse(root->_left, key);
}
else //相等 --> 删除
{
node_pointer deleted_node = root;
if (root->_left == nullptr) //被删节点左子树为空 && 被删节点左右子树都为空
{
root = root->_right;
}
else if (root->_right == nullptr) //被删节点右子树为空 && 被删节点左右子树都为空
{
root = root->_left;
}
else //左右子树都不为空
{
node_pointer min_right = root->_right;
while (min_right->_left) //取被删节点右子树最小值
{
min_right = min_right->_left;
}
//交换数值
swap(min_right->_key, root->_key);
return _erase_Recurse(root->_right, key);
}
delete deleted_node;
return true;
}
}
node_pointer _copy(node_pointer root)
{
if (root == nullptr)
{
return nullptr;
}
node_pointer new_node = new node(root->_key);
new_node->_left = _copy(root->_left);
new_node->_right = _copy(root->_right);
return new_node;
}
void _swap(node_pointer& self, node_pointer& other)
{
node_pointer tmp = self;
self = other;
other = tmp;
}
private:
node_pointer _root;
};
}
4. 时间复杂度分析
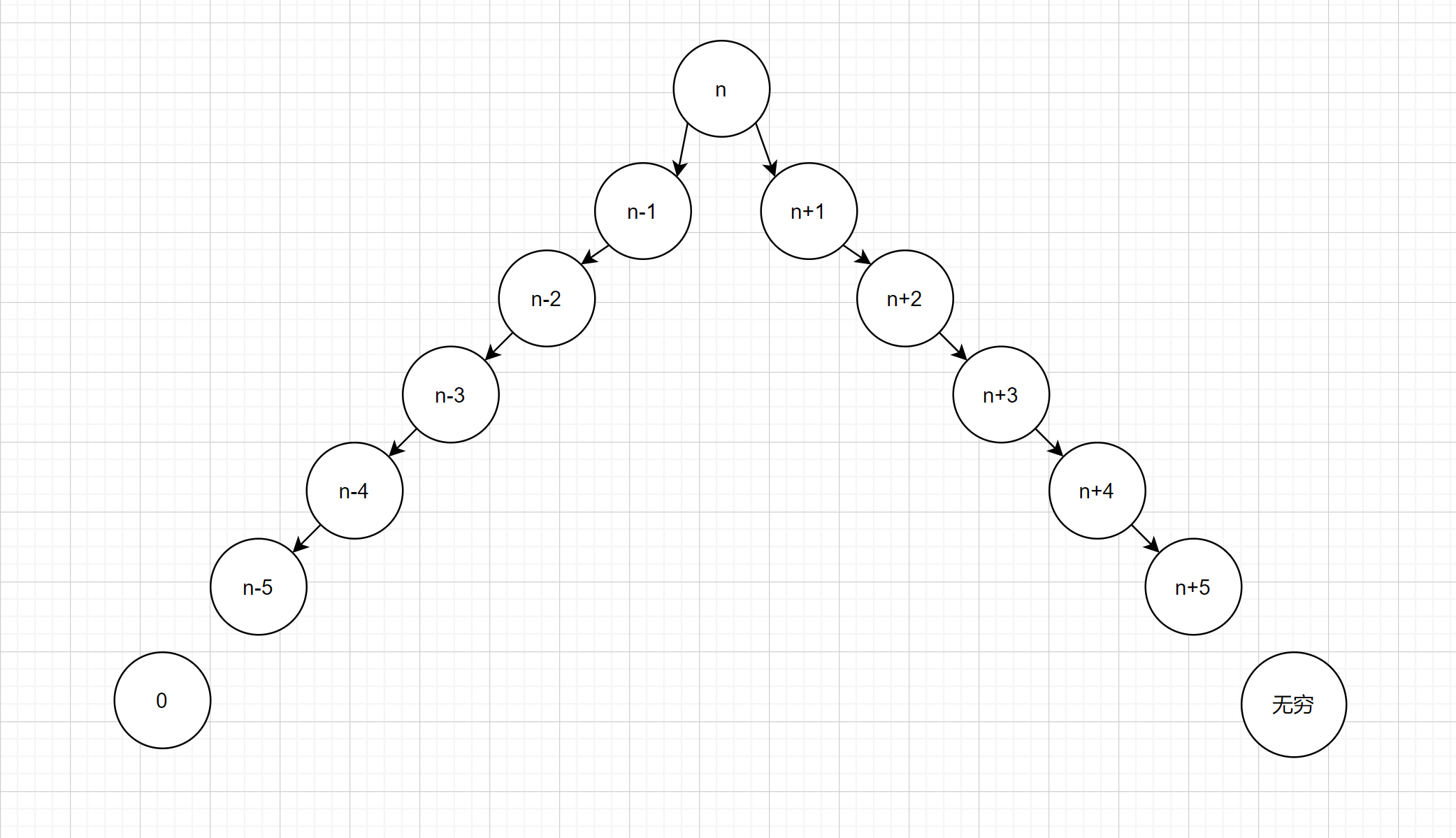
增删查改时间复杂度:O(N)
5. 简单应用
5.1 字典搜索
namespace key_value
{
template <class KEY, class VALUE>
struct node
{
struct node<KEY, VALUE>* _left;
struct node<KEY, VALUE>* _right;
KEY _key;
VALUE _value;
node(const KEY& key, const VALUE& value)
:_left(nullptr)
, _right(nullptr)
, _key(key)
, _value(value)
{}
};
template <class KEY, class VALUE>
class binary_search_tree
{
private:
typedef struct node<KEY, VALUE> node;
typedef node* node_pointer;
public:
binary_search_tree()
:_root(nullptr)
{}
~binary_search_tree()
{
_destory(_root);
}
void _destory(node_pointer root)
{
if (root == nullptr)
{
return;
}
_destory(root->_left);
_destory(root->_right);
delete root;
root = nullptr;
}
bool insert_nonRecurse(const KEY& key, const VALUE& value)
{
//a. 树为空
if (_root == nullptr)
{
_root = new node(key, value);
return true;
}
//b. 树不为空,按性质插入
node_pointer cur = _root;
node_pointer parent = nullptr;
//b.1 找合适位置
while (cur != nullptr)
{
if (key > cur->_key) //b.1.1 key > cur->_key --> 右遍历
{
parent = cur;
cur = cur->_right;
}
else if (key < cur->_key) //b.1.2 key < cur->_key --> 左遍历
{
parent = cur;
cur = cur->_left;
}
else //b.1.3 相等 --> false
{
return false;
}
}
//b.2 连接
cur = new node(key, value);
if (key > parent->_key) //b.2.1 key > parent_key --> 右连接
{
parent->_right = cur;
}
else //b.2.2 key < parent_key --> 左连接
{
parent->_left = cur;
}
return true;
}
node_pointer find(const KEY& key)
{
node_pointer cur = _root;
while (cur != nullptr)
{
if (key > cur->_key)
{
cur = cur->_right;
}
else if (key < cur->_key)
{
cur = cur->_left;
}
else
{
return cur;
}
}
return nullptr;
}
bool erase_nonRecurse(const KEY& key)
{
node_pointer parent = nullptr;
node_pointer cur = _root;
while (cur != nullptr)
{
if (key > cur->_key) //右遍历
{
parent = cur;
cur = cur->_right;
}
else if (key < cur->_key) //左遍历
{
parent = cur;
cur = cur->_left;
}
else //相等 --> 删除
{
/*被删除节点要区分是在其父节点的左子树还是右子树中*/
if (cur->_left == nullptr) //左子树为空 && 左右子树都为空
{
if (cur == _root) //头节点处理
{
_root = cur->_right;
}
else
{
if (parent->_left == cur) //被删除节点在父节点左子树
{
parent->_left = cur->_right;
}
else //被删除节点在父节点右子树
{
parent->_right = cur->_right;
}
}
delete cur;
}
else if (cur->_right == nullptr) //右子树为空 && 左右子树都为空
{
if (cur == _root) //头节点处理
{
_root = cur->_left;
}
else
{
if (parent->_left == cur) //被删除节点在父节点左子树
{
parent->_left = cur->_left;
}
else //被删除节点在父节点右子树
{
parent->_right = cur->_left;
}
}
delete cur;
}
else //左右子树都不为空 (策略:右子树最小值交换)
{
node_pointer min_right = cur->_right;
node_pointer parent_min_right = cur;
while (min_right->_left) //取右子树最小值节点
{
parent_min_right = min_right;
min_right = min_right->_left;
}
swap(min_right->_key, cur->_key);
//被删除节点父节点和其节点右子树连接(支持原因:右子树最小值只可能拥有右子树不可能拥有左子树)
if (parent_min_right->_left == min_right) //右子树最小值节点(被删除节点)在其父节点左子树
{
parent_min_right->_left = min_right->_right;
}
else //右子树最小值节点在其父节点右子树
{
parent_min_right->_right = min_right->_right;
}
delete min_right;
}
return true;
}
}
return false;
}
void inOrder()
{
_inOrder(_root);
cout << endl;
}
private:
void _inOrder(node_pointer root)
{
if (root == nullptr)
return;
_inOrder(root->_left);
cout << root->_key << " " << root->_value << endl;
_inOrder(root->_right);
}
private:
node_pointer _root;
};
void test()
{
binary_search_tree<string, string> dict;
dict.insert_nonRecurse("apple", "苹果");
dict.insert_nonRecurse("banana", "香蕉");
dict.insert_nonRecurse("pear", "梨子");
dict.insert_nonRecurse("orange", "橙子");
dict.insert_nonRecurse("strawberry", "草莓");
dict.insert_nonRecurse("pitaya", "火龙果");
dict.insert_nonRecurse("tangerine", "橘子");
string str;
while (cin >> str)
{
node<string, string>* ret = dict.find(str);
if (ret != nullptr)
cout << ret->_key << "->" << ret->_value << endl;
else
cout << "找不到" << endl;
}
}
}
5.2 统计次数
namespace key_value
{
template <class KEY, class VALUE>
struct node
{
struct node<KEY, VALUE>* _left;
struct node<KEY, VALUE>* _right;
KEY _key;
VALUE _value;
node(const KEY& key, const VALUE& value)
:_left(nullptr)
, _right(nullptr)
, _key(key)
, _value(value)
{}
};
template <class KEY, class VALUE>
class binary_search_tree
{
private:
typedef struct node<KEY, VALUE> node;
typedef node* node_pointer;
public:
binary_search_tree()
:_root(nullptr)
{}
~binary_search_tree()
{
_destory(_root);
}
void _destory(node_pointer root)
{
if (root == nullptr)
{
return;
}
_destory(root->_left);
_destory(root->_right);
delete root;
root = nullptr;
}
bool insert_nonRecurse(const KEY& key, const VALUE& value)
{
//a. 树为空
if (_root == nullptr)
{
_root = new node(key, value);
return true;
}
//b. 树不为空,按性质插入
node_pointer cur = _root;
node_pointer parent = nullptr;
//b.1 找合适位置
while (cur != nullptr)
{
if (key > cur->_key) //b.1.1 key > cur->_key --> 右遍历
{
parent = cur;
cur = cur->_right;
}
else if (key < cur->_key) //b.1.2 key < cur->_key --> 左遍历
{
parent = cur;
cur = cur->_left;
}
else //b.1.3 相等 --> false
{
return false;
}
}
//b.2 连接
cur = new node(key, value);
if (key > parent->_key) //b.2.1 key > parent_key --> 右连接
{
parent->_right = cur;
}
else //b.2.2 key < parent_key --> 左连接
{
parent->_left = cur;
}
return true;
}
node_pointer find(const KEY& key)
{
node_pointer cur = _root;
while (cur != nullptr)
{
if (key > cur->_key)
{
cur = cur->_right;
}
else if (key < cur->_key)
{
cur = cur->_left;
}
else
{
return cur;
}
}
return nullptr;
}
bool erase_nonRecurse(const KEY& key)
{
node_pointer parent = nullptr;
node_pointer cur = _root;
while (cur != nullptr)
{
if (key > cur->_key) //右遍历
{
parent = cur;
cur = cur->_right;
}
else if (key < cur->_key) //左遍历
{
parent = cur;
cur = cur->_left;
}
else //相等 --> 删除
{
/*被删除节点要区分是在其父节点的左子树还是右子树中*/
if (cur->_left == nullptr) //左子树为空 && 左右子树都为空
{
if (cur == _root) //头节点处理
{
_root = cur->_right;
}
else
{
if (parent->_left == cur) //被删除节点在父节点左子树
{
parent->_left = cur->_right;
}
else //被删除节点在父节点右子树
{
parent->_right = cur->_right;
}
}
delete cur;
}
else if (cur->_right == nullptr) //右子树为空 && 左右子树都为空
{
if (cur == _root) //头节点处理
{
_root = cur->_left;
}
else
{
if (parent->_left == cur) //被删除节点在父节点左子树
{
parent->_left = cur->_left;
}
else //被删除节点在父节点右子树
{
parent->_right = cur->_left;
}
}
delete cur;
}
else //左右子树都不为空 (策略:右子树最小值交换)
{
node_pointer min_right = cur->_right;
node_pointer parent_min_right = cur;
while (min_right->_left) //取右子树最小值节点
{
parent_min_right = min_right;
min_right = min_right->_left;
}
swap(min_right->_key, cur->_key);
//被删除节点父节点和其节点右子树连接(支持原因:右子树最小值只可能拥有右子树不可能拥有左子树)
if (parent_min_right->_left == min_right) //右子树最小值节点(被删除节点)在其父节点左子树
{
parent_min_right->_left = min_right->_right;
}
else //右子树最小值节点在其父节点右子树
{
parent_min_right->_right = min_right->_right;
}
delete min_right;
}
return true;
}
}
return false;
}
void inOrder()
{
_inOrder(_root);
cout << endl;
}
private:
void _inOrder(node_pointer root)
{
if (root == nullptr)
return;
_inOrder(root->_left);
cout << root->_key << " " << root->_value << endl;
_inOrder(root->_right);
}
private:
node_pointer _root;
};
void test()
{
string arr[] = { "西瓜", "西瓜", "苹果", "西瓜", "苹果", "苹果", "西瓜", "苹果", "香蕉", "苹果", "香蕉", "梨" };
key_value::binary_search_tree<string, int> countTree;
for (auto str : arr)
{
auto ret = countTree.find(str);
if (ret == nullptr)
{
countTree.insert_nonRecurse(str, 1);
}
else
{
ret->_value++;
}
}
countTree.inOrder();
}
}




![策略设计模式(Strategy Pattern)[论点:概念、组成角色、相关图示、示例代码、适用场景]](https://img-blog.csdnimg.cn/b104d2b4f10048a6b6eba7efa7d89542.png)