系列综述:
💞目的:本文是个人学习多边形裁剪知识整理的,整理期间努力理解论文作者含义,并增加了自己的详述和注解。
🥰来源:材料主要源于多边形裁剪相关论文进行的,每个知识点的学习和深入主要参考各平台大佬的文章
🤭结语:如果有帮到你的地方,就点个赞和关注一下呗,谢谢🎈🎄🌷!!!
文章目录
- 概述
- 基本概念
- 国外著名多边形裁剪算法
- 矩形窗口裁剪算法
- Greiner-Hormann算法
- Weiler-Atherton裁剪算法
- Sutherland-Hodgman算法
- 其他算法
- 国内著名多边形裁剪算法
- 1996鲍虎军,彭群生. 一个有效的多边形裁剪算法
- 2003刘勇奎,高云,黄有群. 一个有效的多边形裁剪算法
- 2002陆国栋,邢世海,彭群生. 基于顶点编码的多边形窗口线裁剪高效算法
- 2006白晨. 一种任意多边形的裁剪算法
- 2006付迎春,袁修孝.一种有效的任意多边形裁剪算法
- 数控系统的工艺融合论文思路
- 问题
- 规则
- 思路(有问题)
- 思路2
- 特殊问题
- idea
- 线裁剪算法
- 参考博客
😊点此到文末惊喜↩︎
概述
基本概念
- 多边形的类型
- 前提:多边形的每一个内角都是由两条相邻边形成的
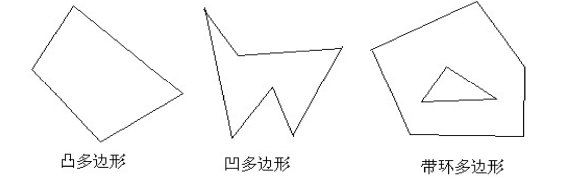
- 凸多边形:多边形的所有内角均小于180°
- 凹多边形:多边形bm存在内角大于180°的内角
- 带内环的多边形

- 国外著名多边形裁剪算法
- 矩形窗口裁剪算法
- Greiner-Hormann裁剪算法《Efficient clipping of arbitrary polygons》?
- Sutherland-Hodgman算法 《Reentrant polygon clipping》
- Vatti裁剪算法《A Generic Solution to Polygon Clipping》
- Weiler-Atherton裁剪算法《Hidden surface removal using polygon area sorting》
- 国内著名多边形裁剪算法
- 鲍虎军,彭群生. 一个有效的多边形裁剪算法
- 刘勇奎,高云,黄有群. 一个有效的多边形裁剪算法
- 陆国栋,邢世海,彭群生. 基于顶点编码的多边形窗口线裁剪高效算法
- 白晨.一种任意的多边形裁剪算法
国外著名多边形裁剪算法
矩形窗口裁剪算法
- 矩形裁剪的基本规则
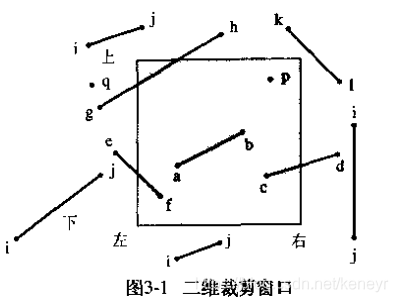
- 如果直线的两个端点都在窗口边界之内,如ab,则直线保留
- 如果直线的一个端点在窗口边界之内,另一个端点在窗口边界之外,如ef,则应从直线与边界的交点处裁剪掉边界之外的线段
- 如果直线的两个端点都在窗口边界之外,有两种情况:
- 一种情况如ij,直线全部在窗口之外,应该全部裁减掉;
- 另一种情况如gh,直线横穿窗口边界,应该保留相交的片段,裁减掉剩余的片段
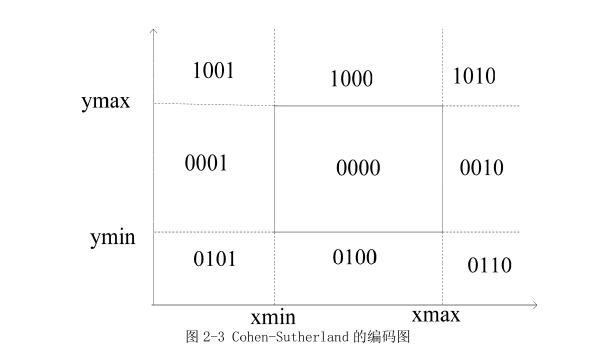
- 1968Cohen-Sutherland裁剪算法(编码裁剪算法)
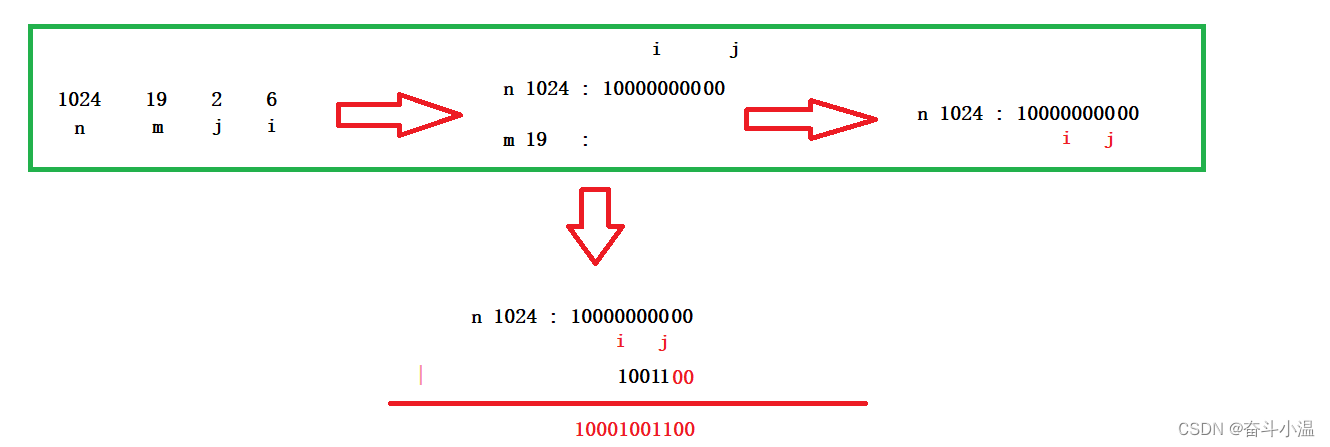
- 先对端点P1和P2进行编码,P1的编码 : code1 P2的编码 : code2
- 完全在窗口内,则有 code1 | code2 = 0
- 完全在窗口外,则有 code1 & code2 != 0
- 与窗口相交,求交,将窗口外的线段丢弃,再进行裁剪
- Newman-Sproul直线段中点分割裁剪算法
- 先对端点P1和P2进行编码,P1的编码 : code1 P2的编码 : code2
- 完全在窗口内,则有 code1 | code2 = 0
- 完全在窗口外,则有 code1 & code2 != 0
- 上面两种情况都不符合,则求交点。
- P与P1同侧,则交点在P和P2之间,则将P点的坐标赋值给P1;
- P与P2同侧,则交点在P和P1之间,则将P点的坐标赋值给P2。
- 之后递归对中点进行分割,则可以收敛到交点。
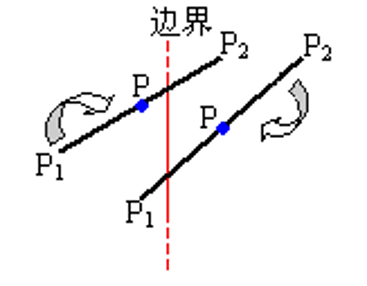
- 梁友栋-Barsky裁剪算法
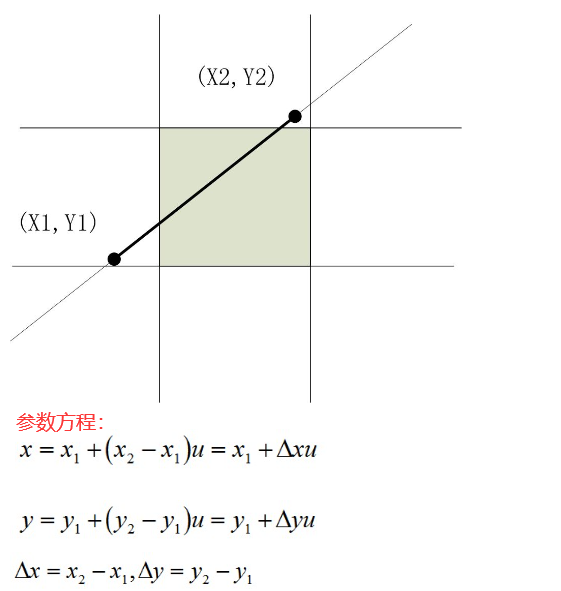

Greiner-Hormann算法
- 特点
- 每个多边形均采用双链表进行表示,每找到一个交点就分别插入实体多边形和裁剪多边形的
- 基于布尔运算的多边形裁剪算法,它可以处理自相交和重叠的情况。
Weiler-Atherton裁剪算法
- 特点
- 裁剪窗口和被裁剪多边形可以是任意多边形:凸的、凹的
- 相比之前的多边形裁剪算法,平均性能最好的
- 在有重合边和与多边形顶点相交时会出现失效的情况,且处理带环多边形之间的裁剪效率低。
- 算法流程
- 从被裁剪多边形的一个入点开始,碰到入点,则沿着被裁剪多边形按顺时针方向搜集出点,并将出点放如输出多边形顶点序列(为防止在处理分裂多边形时失效,算法要将搜集过的入点的入点标记删去,以免重复跟踪。)
- 再沿着裁剪窗口按顺时针方向搜集顶点序列,直到遇到下一个入点,此过程中如遇到被裁剪多边形的顶点,则将顶点按照查找的顺序插入到输出顶点序列中。
- 按上述规则,交替地沿着被裁剪多边形和裁剪窗口的边界行进,直到回到起始点。
- 收集到的全部顶点序列就是裁剪所得的多边形。
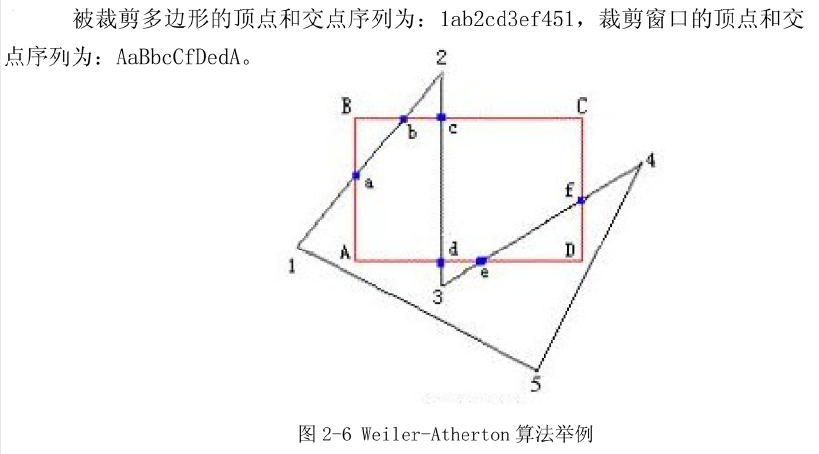
Sutherland-Hodgman算法
- 基本概述
- Sutherland-Hodgman算法也叫逐边裁剪法,该算法是萨瑟兰德(I.E.Sutherland)和霍德曼(Hodgman)在1974年提出的。这种算法采用了分割处理、逐边裁剪的方法
- 特点
- 被裁剪多边形可以是任意凸多边形或凹多边形,裁剪窗口不局限于矩形,可以是任意凸多边形。
- 基本思想
- 窗口的一条边以及延长线构成的裁剪线该线把平面分成两个部分:可见一侧;不可见一侧。多边形的各条边的两端点S、P。它们与裁剪线的位置关系只有四种
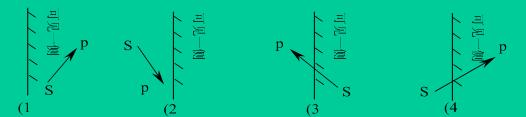
- 情况(1):被裁减的线段端点均在可见一侧,则只输出
顺时针方向的P点 - 情况(2):被裁减的线段均在不可见一侧,则不输出顶点
- 情况(3):被裁减的线段端点在两侧,则只输出线段SP与裁剪窗口边界的1个交点I;
- 情况(4):被裁减的线段端点在两侧,则输出P端点和线段与裁剪窗口边界的1个交点I;
- 情况(1):被裁减的线段端点均在可见一侧,则只输出
- 窗口的一条边以及延长线构成的裁剪线该线把平面分成两个部分:可见一侧;不可见一侧。多边形的各条边的两端点S、P。它们与裁剪线的位置关系只有四种
- 示例
- 顺时针访问多边形各条边,可以以上面的基本思想来对上图多边形进行裁剪,可以得到正确的结果
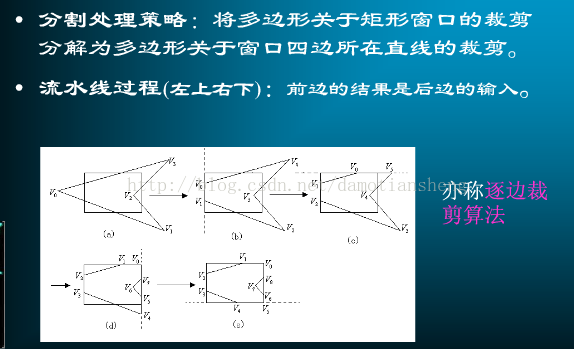
- 顺时针访问多边形各条边,可以以上面的基本思想来对上图多边形进行裁剪,可以得到正确的结果
- 具体算法设计
//点在有向线段那侧
/*
向量叉积法
为简单计,测试点表示为P点。假设窗口边界方向为顺时针,如图中所示,对于其中任一边界向量,从向量起点A向终点B看过去:
如果被测试点P在该边界线右边(即内侧),AB×AP的方向与X-Y平面垂直并指向屏幕里面,即右手坐标系中Z轴的负方向。
反过来,如果P在该边界线的左边(即外侧),这时AB×AP的方向与X-Y平面垂直并指向屏幕外面,即右手坐标系中Z轴的正方向。
设:点P(x,y)、点A(xA,yA)、点B(xB,yB),
向量AB={(xB-xA),(yB-yA)},
向量AP={(x-xA),(y-yA)},
那么AB×AP的方向可由下式的符号来确定:
V=(xB-xA)·(y-yA)-(x-xA)·(yB-yA) // V为AB叉乘AP的结果向量中的z分量
因此,当V≤0时,P在边界线内侧;
而V>0时,P在边界线外侧。
*/
typedef point
{
int x;
int y;
}RtPoint;
typedef struct
{
RtPoint sp; //裁剪窗口边界向量起点
RtPoint ep; //裁剪窗口边界向量终点
}_RtInSide;
static int _RtInSide(RtVector vector, RtPoint point) // 计算上面的V,vector为裁剪窗口边界向量,point为上面的p点
{
return (vector.ep.x - vector.sp.x) * (point.y - vector.sp.y) - (vector.ep.y - vector.sp.y) * (point.x - vector.sp.x);
}
//多边形点必须是顺时针方向
// src保存的是裁剪窗口坐标点,应该是顺时针方向保存,num为裁剪窗口边界数量,*dest保存裁剪后的多边形顶点数组,*total为*dest大小
int rtPrunePSH(RtPoint* src, int num, RtPoint** dest, int* total)
{
int i = 0, j = 0, k = -1, flag = 0;
RtPoint start, stop;//被剪裁多边形的边向量起点和终点
RtPoint sp, ep;//剪裁窗口边界向量的起点和终点
RtPoint* temp = NULL; // temp保存针对某一裁剪窗口边界裁剪后的新坐标
temp = (RtPoint*)malloc(sizeof(RtPoint) * 3 * (*total));
if (temp == NULL) return -1;
sp = *(src + num - 1);
for ( i = 0; i < num; i++)//剪裁窗口
{
ep = *(src + i);
start = *((*dest) + *total - 1);
flag = _RtInSide(rtVector(sp, ep), start) > 0 ? 0 : 1; //在外侧,flag为0,在内侧时flag为1
for ( j = 0; j < *total; j++)//被剪裁的多边形
{
stop = *((*dest) + j);
if (_RtInSide(rtVector(sp, ep), stop) <= 0)//当前第i个顶点是否在边界内侧
{
if (flag == 0)/*前一个点在外侧吗?*/
{
flag = 1;/*从外到内的情况,将标志置1,作为下一次循环的前一点标志*/
k++;
CRtPoint<double> point;
CRtPoint<int> st(sp.x, sp.y), et(ep.x, ep.y);
CRtLine<int> v1(st, et);//v1为由窗口边界向量起点sp和终点ep组成的直线
st.SetData(start.x, start.y);
et.SetData(stop.x, stop.y); //v2为由多边形当前边起点start和终点stop组成的直线
CRtLine<int> v2(st, et);
v2.Intersect(v1,point); //两直线求交运算,交点保存到point数组里面
(temp + k)->x = point[0];/*将交点放入新多边形*/
(temp + k)->y = point[1];
}
k++;
*(temp + k) = stop;/*将当前点pi放入新多边形*/
}
else
{
if (0 != flag)/*前一个点在内侧吗?*/
{
flag = 0;/*从内到外的情况,将标志置1,作为下一次循环的前一点标志*/
k++;
CRtPoint<double> point; // 同上面一样
CRtPoint<int> st(sp.x, sp.y), et(ep.x, ep.y);
CRtLine<int> v1(st, et);
st.SetData(start.x, start.y);
et.SetData(stop.x, stop.y);
CRtLine<int> v2(st, et);
v2.Intersect(v1,point);
(temp + k)->x = point[0];/*将交点放入新多边形*/
(temp + k)->y = point[1];
}
}
start = stop;/*将当前点作为下次循环的前一点*/
}
sp = ep;
*total = k + 1; // k+1为一次裁剪后生成的新坐标点的数量
memcpy(*dest, temp, sizeof(RtPoint) * (*total));
k = -1;
}
return 0;
}
其他算法
- Vatti是一个利用扫描线和优先队列的多边形裁剪算法,它可以处理任意形状的多边形
- Polygon Reconstruction算法:这是一个可以从一组线段重建多边形的算法,它可以处理裁剪后产生的不连通的多边形。
- Line Clipping算法:这是一个可以将线段按照一个多边形进行裁剪的算法,它可以处理任意形状的多边形1。
- Cyrus-Beck算法:这是一个针对任意凸多边形裁剪区域的线段裁剪算法,它使用参数化方程和点积来判断线段是否可见23。
国内著名多边形裁剪算法
1996鲍虎军,彭群生. 一个有效的多边形裁剪算法
- 算法流程:
- 两个多边形分别为P和Q,为每个多边形建立一个双向的环形链表。
- 从被裁剪多边形Q的链表中取出一个状态为in的线段,从该线段出发,按照顺时针跟踪多边形表,直到发现下一线段状态为out为止
2003刘勇奎,高云,黄有群. 一个有效的多边形裁剪算法
- 特点
- 可适应于一般多边形、凹多边形和具有内孔的多边形
- 不仅可以求多边形的交(多边形裁剪),还可以求出多边形的并和差
- 使用单链表作为基本数据结构
- 可以求具有多个分立多边形的情况
- 基本概念
- 基本数据结构:每个多边形用一个循环单链表进行表示,单链表中的节点是多边形的一个顶点,并且顺时针顺序存储 (循环的意义是多边形是封闭的)
- 顺右逆左:边的方向按
顺时针走则规定右边为内部,边的方向按逆时针走则规定左边为内部。具有孔洞的多边形,内部以相反的规则进行内外判定 - 设I是多边形S和C的交点,C固定不动S沿边界走
- 进点:S从C的外部到内部形成的交点I
- 出点:S从C的内部到外部形成的交点I
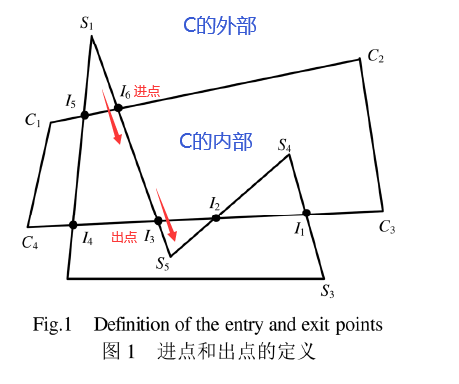
- 进点和出点的判定
- 设
S
i
S_i
Si为
C的外点,则 S i S_i Si沿S的边界与C的第一个交点必然是进点 - 设
S
i
S_i
Si为
C的内点,则 S i S_i Si沿S的边界与C的第一个交点必然是出点 - 进点和出点是
依次出现的,所以只要判定第一个交点是进点or出点,其他交点按序即可确定进出性
- 设
S
i
S_i
Si为
- 数据结构的定义
// 顶点的二维坐标 struct coordinate{ int x; int y; } // 顶点/交点的结构体 struct vertex{ coordinate cord;// 顶点坐标 bool inters;// 本身是否为交点 bool used;// 用于有多个输出多边形时,初值为0,输出后置1 struct vertex *next1;// 插入到实体多边形链表 struct vertex *next2;// 若为交点则启用,插入到裁剪多边形链表 } - 算法基本流程
- 阶段1:判断及计算第一个交点,并由其进出性判断两个多边形是否同向(原因是下面定理)。如果不同向则将裁剪多边形链表反向,然后将该交点插入到两个多边形的链表中
- 阶段2:依次以实体多边形的每一个边对裁剪多边形进行直线裁剪操作,判断及计算其余交点,并以正确的顺序插入到两个多边形的链表中
- 阶段3:遍历整个链表,输出最终结果
- 定理
- 定理1:如果两个相交的多边形的边取向相同(均为顺时针或逆时针),则对一个多边形是进点的交点,对于另一个多边形必是出点(文中已证明)
- 定理2:交点的进出性是按顺序依次交替的
- 结论:两个同向多边形,交点的进出性只需要标记对于其中一个多边形的即可,对于另一个多边形进出性与其相反。
- 边裁剪算法
- 特殊情况的处理
- 参考处理方法
- 通过在链表上减少或增加交点,来保持进点和出点的交替出现。处理复杂
- 对重合边的一个顶点或交点相同的顶点进行很小的移动来避免特殊情况。增加误差
- 结论方法
- 如果重合顶点数一数裁剪多边形,则只将该顶点的y坐标±一个单位使该点上下移动,因为实体多边形的当前边已经错切成水平线,所以不会仍然重合。如果重合顶点属于实体多边形,则只将该顶点的x坐标±一个单位使该点左右移动即可避开裁剪多边形的边
- 参考处理方法
- 与其他算法的比较
- 空间复杂度:相比于Vatti和Greiner-Hormann算法只占用了一半的存储单位
- 时间复杂度 :由于减少域的设置量而节省了大量时间
2002陆国栋,邢世海,彭群生. 基于顶点编码的多边形窗口线裁剪高效算法
- 编码技术:以裁剪窗口为参照系,延长矩形窗口的四条边,将平面划分为九个区域,根据线段所在区域进行线段的编码。通过这种静态预编码,可以在运行时简洁高效的判断线段的状态。
- 裁剪算法目标:
- 尽量避免求交运算
- 尽可能加快求交进程
- 快速有效处理特殊相交情况
- 裁剪分区
- 包围盒:将上下左右的最外侧顶点连接形成的正方形,用于快速舍弃无用裁剪边。但是程序中可以通过对称处理,最终将四种情况简化成两种。
- P点取裁剪直线与多边形窗口交点,在具体实现时,算法具有两个分支
|k| > 1:|k| ≤ 1:
- 通过窗口编码技术可以排除大部分与多边形窗口不相交的裁剪直线,只剩下部分与窗口不相交的被裁减直线和所有的与窗口相交的被裁减直线
- 部分与窗口不相交线段的消减:判断交点是否位于直线的延迟线上,如果在则为无效交点
- 特殊情况
- 交点是顶点的情况
- 裁剪线段两端位于多边形异侧,需要保存交点
- 裁剪线段两端位于多边形同侧,不需要保存交点
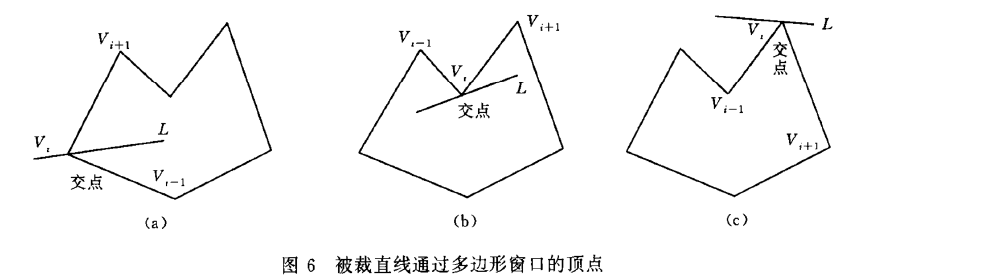
- 被裁剪直线与窗口的某一边重合
- 基本:构成包围盒的多边形顶点必是凸顶点,求以它们为顶点的向量的叉积,其它顶点的向量叉积若与极值点的向量叉积相同则为凸顶点,否则为凹顶点。
- 凸顶点计入交点数据,凹顶点不需计入交点数组。
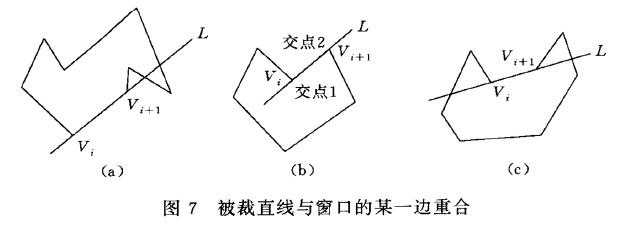
- 交点是顶点的情况
- 算法流程
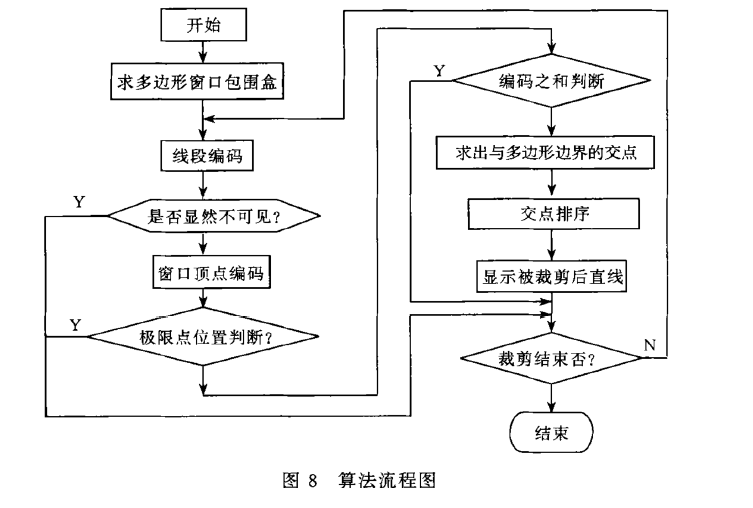
- 总结:本文从多边形窗口的
线裁剪的本质特征出发(忽略了整体性?),借鉴了区域编码技术,实现了多边形裁剪算法稳定性和效率上的提高。
2006白晨. 一种任意多边形的裁剪算法
- 裁剪定义:从图形中识别出区域内外部分的过程
- 计算机速度需求:对于要求图形更新速度的情况下,一旦计算时间的延迟超过了容忍的程度,则失去了工程意义
- 二维裁剪
- 判断是否
线段与裁剪窗口相交,充分必要条件是线段中有点在裁剪窗口内部。实际计算机工程中不可能通过判断线段中所有的点的情况,这样极大的影响算法效率和精度。 - 曲线可以通过折线段进行拟合
- 判断是否
- 不带环多边形之间的裁剪过程
- 数据结构
// 各交点的信息:其他被裁剪多边形为S1,裁剪窗口为S2 struct dot{ double x;// 坐标 double y; double t1;// 交点在S1上的位置参数 double t2;// 交点在S2上的位置参数 int l1;// 标记交点在S1上的哪条线段 int l2;// 标记交点在S2上的哪条线段 int used;// 标记交点在原顶点序列中是否已经使用 }- 求裁剪多边形和裁剪窗口的交点:依次取出组成S1和S2边界对各线段两两相交(暴力?),通过各线段的参数方程计算结果,如方程无解,则两线段不相交,如果有解,则求出交点,并将所有的交点按照dot结构放入一个有效交容器vector中
- 多边形边界重合的情况:当线段和多边形两条边界的交点重合时(即多边形两条边界的交点在线段上),如多边形的两条边界都在线段同侧,则有效交点数量为2,如多边形的两条边界分别在线段不同侧,则有效交点数为1.当线段和多边形边界重合时,如与重合线段相邻的两条多边形边界在重合线段同一侧,则有效交点为1,如与重合线段相邻的两条多边形边界在重合线段不同侧,则有效交点为2。计算有效交点的目的是为了判断点P0是否在多边形S内部,如有小交点数是奇数,则P0在多边形S内部,如有效交点数是偶数,则P0在多边形外部。
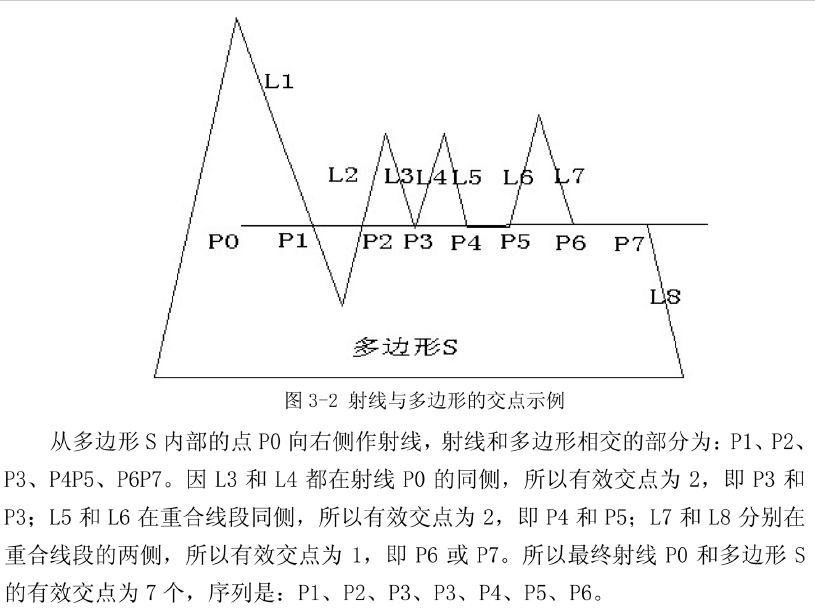
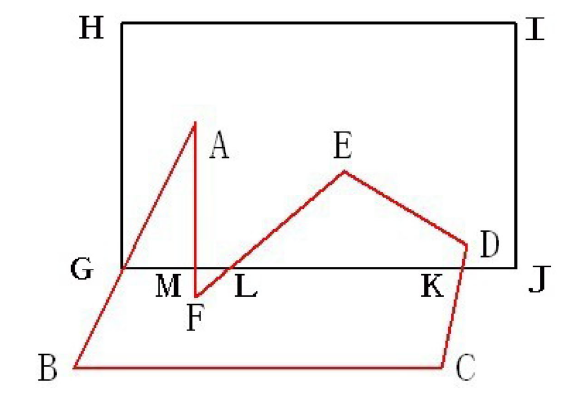
- 求被裁剪多边形和裁剪窗口相交后的基本线段:将
交点分别插入被裁剪多边形S1和裁剪窗口多边形S2中,再分别对于两个点序列进行线段区分(两个多边形由多个顶点和两个交点形成的闭合区域),如下S1: G → B → C → K G \rightarrow B \rightarrow C \rightarrow K G→B→C→K、 K → D → E → L K \rightarrow D \rightarrow E \rightarrow L K→D→E→L、 L → F → M L \rightarrow F \rightarrow M L→F→M、 M → A → G M \rightarrow A \rightarrow G M→A→G,而S2为 G → H → I → J → D G \rightarrow H \rightarrow I \rightarrow J \rightarrow D G→H→I→J→D、 K → L K \rightarrow L K→L、 L → M L \rightarrow M L→M、 M → G M \rightarrow G M→G
- 从相关线段组中找到与当前线段夹角最小的线段

- 遍历基本线段单元组,寻找裁剪的结果多边形。从基本线段中找一条没有用于组件多边形的线段作为初试线段,用公示求得它的家教最小的相关线段作为下一条线段,若找到下一条线段和初始相同,则结果多边形找到。
- 判断多边形的内点。通过判断裁剪多边形内一点是否同时在裁剪窗口和被裁剪多边形内部,可以来判定该多边形是否是我们要求的最终裁剪结果。受三点确定一个平面的公理的启发,可以在多边形中取相邻的三个顶点,找到前两个顶点的中点,然后计算这个中点和第三个顶点连接线的中点,那这个点必然是凸多边形内的一点。但假如图形为凹多边形,则有可能此点落到了多边形外部,还需要重新取另外三个相邻顶点,用同样的方法计算内点,直到找到为止。
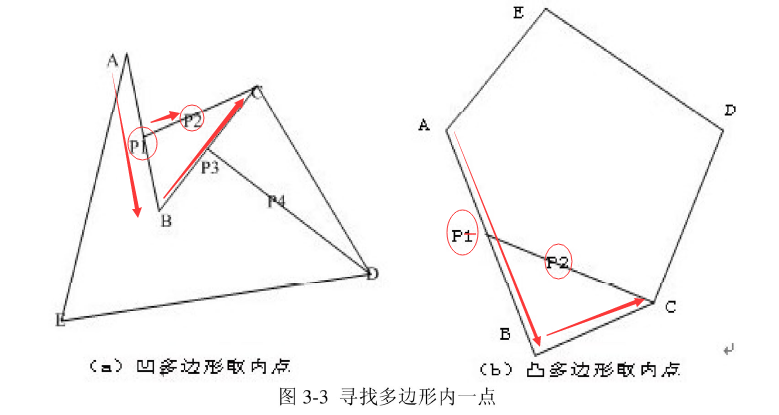
- 删除不合格的多边形
- 删除即不在被裁剪多边形内部也不在裁剪窗口内部的多边形
- 删除被裁剪多边形和裁剪窗口的轮廓多边形
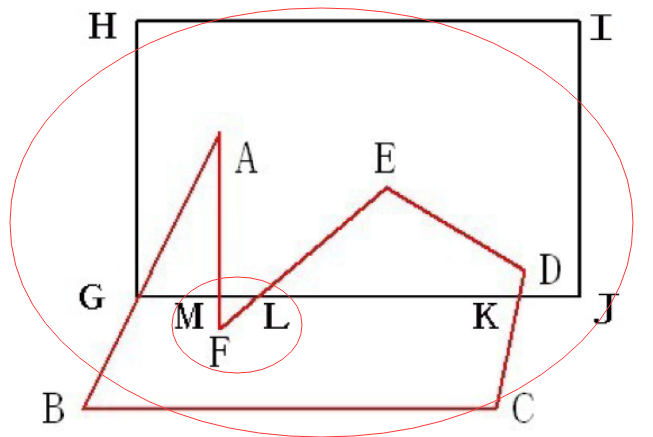
- 最终结果

2006付迎春,袁修孝.一种有效的任意多边形裁剪算法
数控系统的工艺融合论文思路
问题
规则
- 线裁剪类型
- 线段和线段
- 圆弧和圆弧
- 线段和圆弧
思路(有问题)
简单判断实体多边形和裁剪图形是否相交(简单的意思是通过低开销的算法进行不精确的判断)- 不可能出现裁剪图形完全在内部的情况,因为车床肯定是从边界开始加工的
- 如果裁剪图形完全在外部,没有相,根本不需要加工
- 思路1:静态区域编码方式,如Cohen-Sutherland算法。
- 思路2:取裁剪图形和实体图形的最值顶点( x m i n 、 x m a x 、 y m i n 、 y m a x x_{min}、x_{max}、y_{min}、y_{max} xmin、xmax、ymin、ymax),判断是否相交 ( x m i n , y m i n ) ≤ ( x , y ) ≤ ( x m i n , y m i n ) (x_{min}, y_{min}) \leq (x,y) \leq (x_{min}, y_{min}) (xmin,ymin)≤(x,y)≤(xmin,ymin)
- 上面两种思路均无法完全判断,因为存在裁剪后的实体图形的被裁剪区域包含新的裁剪图形的情况
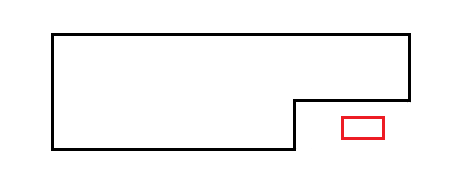
- 判断相交
- 思路1:判断实体多边形节点是否和裁剪多边形有交点(核心是判断是否有顶点在裁剪多边形内)
- 斜向切割: ( x m i n , y m i n ) ≤ ( x , y ) ≤ ( x m a x , y m a x ) (x_{min}, y_{min}) \leq (x,y) \leq (x_{max}, y_{max}) (xmin,ymin)≤(x,y)≤(xmax,ymax)&&将 ( x , y ) (x,y) (x,y)带入线段判断是否在下方
- 矩形切割: ( x m i n , y m i n ) ≤ ( x , y ) ≤ ( x m a x , y m a x ) (x_{min}, y_{min}) \leq (x,y) \leq (x_{max}, y_{max}) (xmin,ymin)≤(x,y)≤(xmax,ymax)
- 圆弧切割: ( x m i n , y m i n ) ≤ ( x , y ) ≤ ( x m a x , y m a x ) (x_{min}, y_{min}) \leq (x,y) \leq (x_{max}, y_{max}) (xmin,ymin)≤(x,y)≤(xmax,ymax)&&将 ( x , y ) (x,y) (x,y)带入圆弧判断是否在下方
- 横向/斜向螺纹切割:相当于给一个线段边界属性的更改(大螺纹如何处理?),判断螺纹的切割是否属于一条实体多边形的边界
- ( x m i n , y m i n ) ≤ ( x , y ) ≤ ( x m i n , y m i n ) (x_{min}, y_{min}) \leq (x,y) \leq (x_{min}, y_{min}) (xmin,ymin)≤(x,y)≤(xmin,ymin)这是一种包装盒的思想,来源于《2002陆国栋,邢世海,彭群生. 基于顶点编码的多边形窗口线裁剪高效算法》,衍生于编码裁剪算法
这个思想无法解决实体多边形顶点不在图形内,但是两个顶点连接成的线段穿过裁剪图形的情况,必须处理线段问题
- 思路1:判断实体多边形节点是否和裁剪多边形有交点(核心是判断是否有顶点在裁剪多边形内)
- 边界遇到节点走路的贪心策略:
- 实体多边形边界线段
逆时针走。 - 通过上一条线段和本线段的x与y的增减性判断线段走向
- 若判断为
x增,则遇到交点,优先向y增的方向走,y不增,其次再向x增的方向走 - 若判断为
y增,则遇到交点,优先向x减的方向走,x不减 ,其次再向y增的方向走
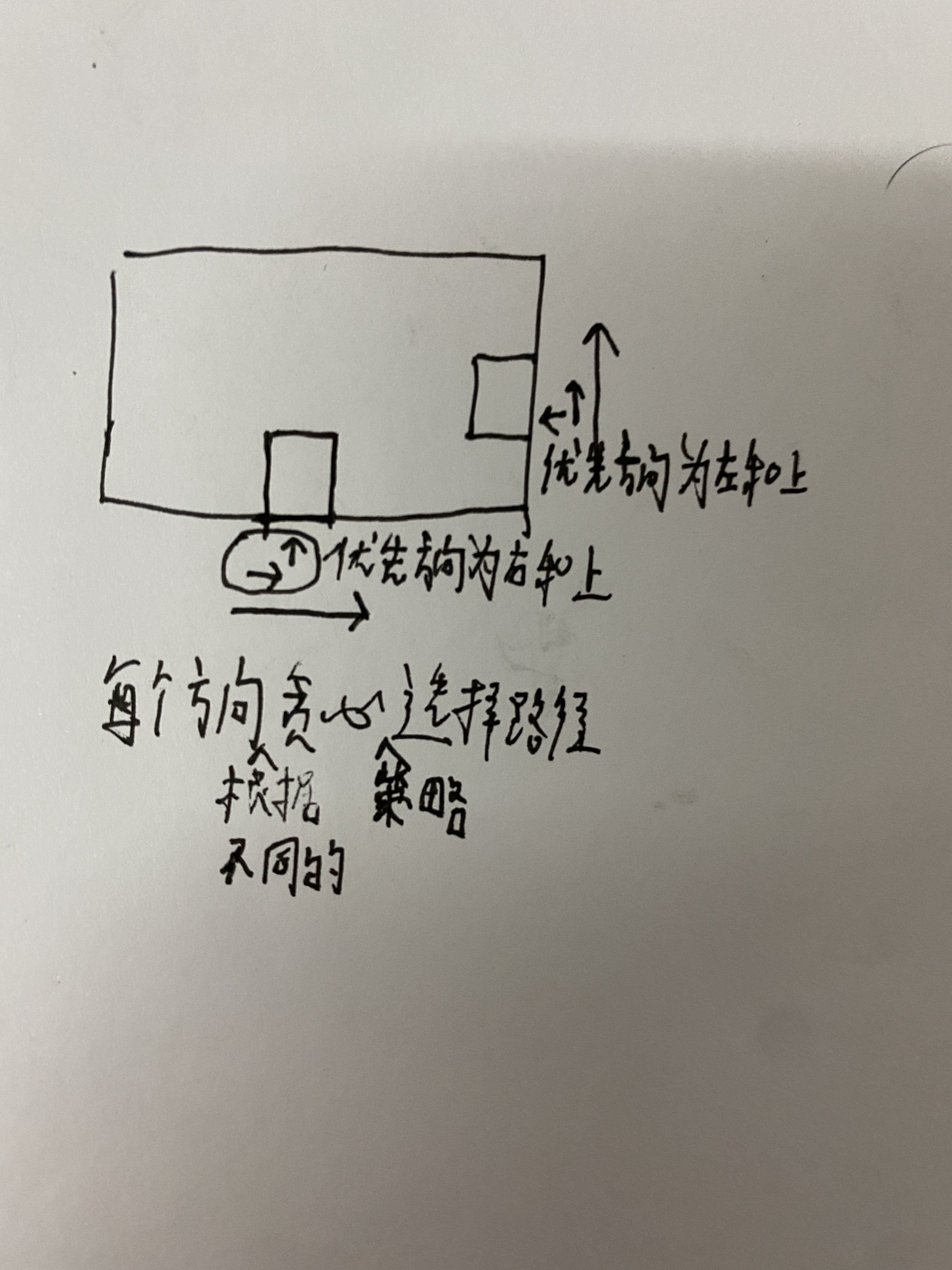
- 若判断为
- 实体多边形边界线段
思路2
- 判断是否含有交点
- 快速排斥
特殊问题
- 交点是顶点的情况
- 被裁剪直线与窗口的某一边重合
idea
- 边所属区分
- 原理:两个多边形使用单链表连接,插入点时区分插入边的所属,实多边形是顺时针,裁剪多边形用逆时针。在按照实多边形的边开始走,碰见裁剪多边形就按照裁剪多边形走,再碰见实体多边形就走实体多边形。即实体多边形和裁剪多边形交换走,最后形成闭环即可。主要点是顶点表示其顺时针到下一个顶点的边的所属
- 问题:边重合后的问题,起始点被裁剪掉的问题
- 本质:每次的进点和出点是一次完整的边裁剪
- 各种裁剪算法思路
- 斜率判断:在被裁剪直线的延长线上取一基准点,然后求多边形裁剪窗口上的每一顶点到该点连线的斜率,从而通过判断被裁剪直线斜率是否在该边两顶点到基准点连线斜率之间,来判定直线与边的关系。
- 交点判断:用参数法求交得出线段及其延长线与多边形各边的交点,然后判断交点是否是有效交点,并根据参数值排序,去掉重复的交点,最后判断以相邻交点为端点的线段的中点是否可见,若是,则此线段可见,若不是,则不可见。
线裁剪算法
用于多边形裁剪中线段求交点

🚩点此跳转到首行↩︎
参考博客
- 如何判别凹多边形
- 多边形裁剪一:Sutherland-Hodgman算法
- Greiner-Hormann的改进
- 裁剪算法——中点分割算法/Liang-Barsky算法
- 图形裁剪——二维裁剪+三维裁剪+Sutherland-Cohen裁剪算法+中点分割算法
- 图形学初步–裁剪算法之Liang-Barsky算法
- 图形学初步–裁剪算法之Liang-Barsky算法
- 待定引用

![洛谷P8772 [蓝桥杯 2022 省 A] 求和 C语言/C++](https://img-blog.csdnimg.cn/aa90339fa213408d915c6e1208818890.png)