证明：“电压电流相位差的余弦值”和“功率因数”相等。

电压电流相位差的余弦值和功率因数相等，这在《电路分析》中给出过结论，但没有给出详细的证明过程。其次，在电气工程师考试中，也会经常遇到。

电压电流相位差：是指电压与电流之间的时间差，用θ表示。

功率因数表示一个负荷所需要的有功功率和视在功率的比值。

即cosφ=P/S，

其中：

P为有功功率

Q为无功功率

S为视在功率：S = U*I

cosφ为功率因数，φ为功率因数角。

下面证明：cosθ= cosφ

1、首先建立数学模型

电压函数：u(t)=Um * sin(ωt+α)，用极坐标表示(Um,∠α)

电流函数：i(t)=Im * sint(ωt+β)，用极坐标表示(Im,∠β)

θ = ∠α- ∠β

电压有效值为U

电流有效置为I

为了便于计算，我们可以将极坐标系顺时针旋转α，得到下图：

 

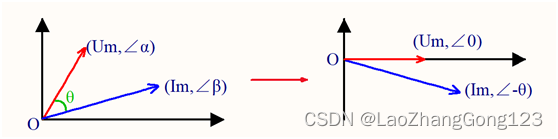
电压函数：u(t)=Um * sin(ωt)，用极坐标表示(Um,∠0)

电流函数：i(t)=Im * sin(ωt-θ)，用极坐标表示(Im,∠-θ)

2、瞬时功率

p(t)=u(t)*i(t)

p(t)=Um * sin(ωt)* Im * sin(ωt-θ)

= Um * Im *[cosθ-cos(2ωt-θ)]/2

= U * I * cosθ- U * I * cos(2ωt-θ)

展开后，瞬时功率为：

p(t)= U * I [cosθ- cosθ* cos(2ωt) - sinθ* sin(2ωt)]

3、有功功率(平均功率)计算

    由于瞬时功率随时间不断变化，工程上应用很不方便,由此引入平均功率。平均功率是指瞬时功率在一个周期内的平均值，又称为有功功率，并用P表示。

令T=2Π/2ω

 

平均功率：P=(1/T)∫p(t)

P=(1/T)∫p(t)=( U*I/T)∫[cosθ-cosθ* cos(2ωt)- sinθ* sin(2ωt)]d(t)

=( U*I/T)∫cosθd(t)-(cosθ*/2ω)∫cos(2ωt) d(2ωt)-(sinθ/2ω)∫sin(2ωt)]d(2ωt)

=U*I*cosθ

因为S = U*I，所以P=S*cosθ,即cosθ=P/S

又因为功率因素cosφ=P/S，所以cosφ = cosθ

有功功率是一个不随时间变化的恒定值，而瞬时功率随时间在不断变化。

4、无功功率

    由于有功功率同X轴平行，无功功率同Y轴平行，因此，有功功率与无功功率的矢量角度为90度，则：

Q * Q  =  S * S  -  P * P

在电工技术中，定义视在功率为：S = U * I

前面计算到有功功率：P = U * I * cosθ

Q * Q  =  (U*I) * (U*I)  -  (U * I * cosθ)*( U * I * cosθ)

      =  (U*I)* (U*I) * [ 1 - cosθ* cosθ]

      =  (U*I*sinθ) * (U*I*sinθ)

因此，无功功率为Q = U * I * sinθ