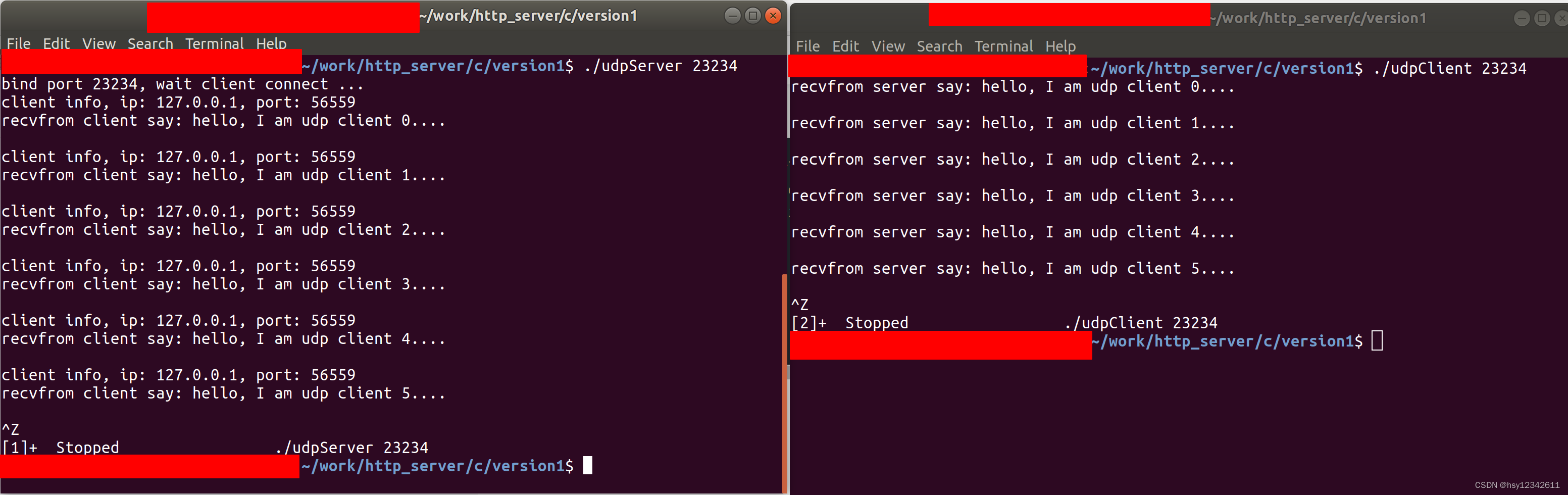
平方计数 - 题目 - Daimayuan Online Judge
题意:
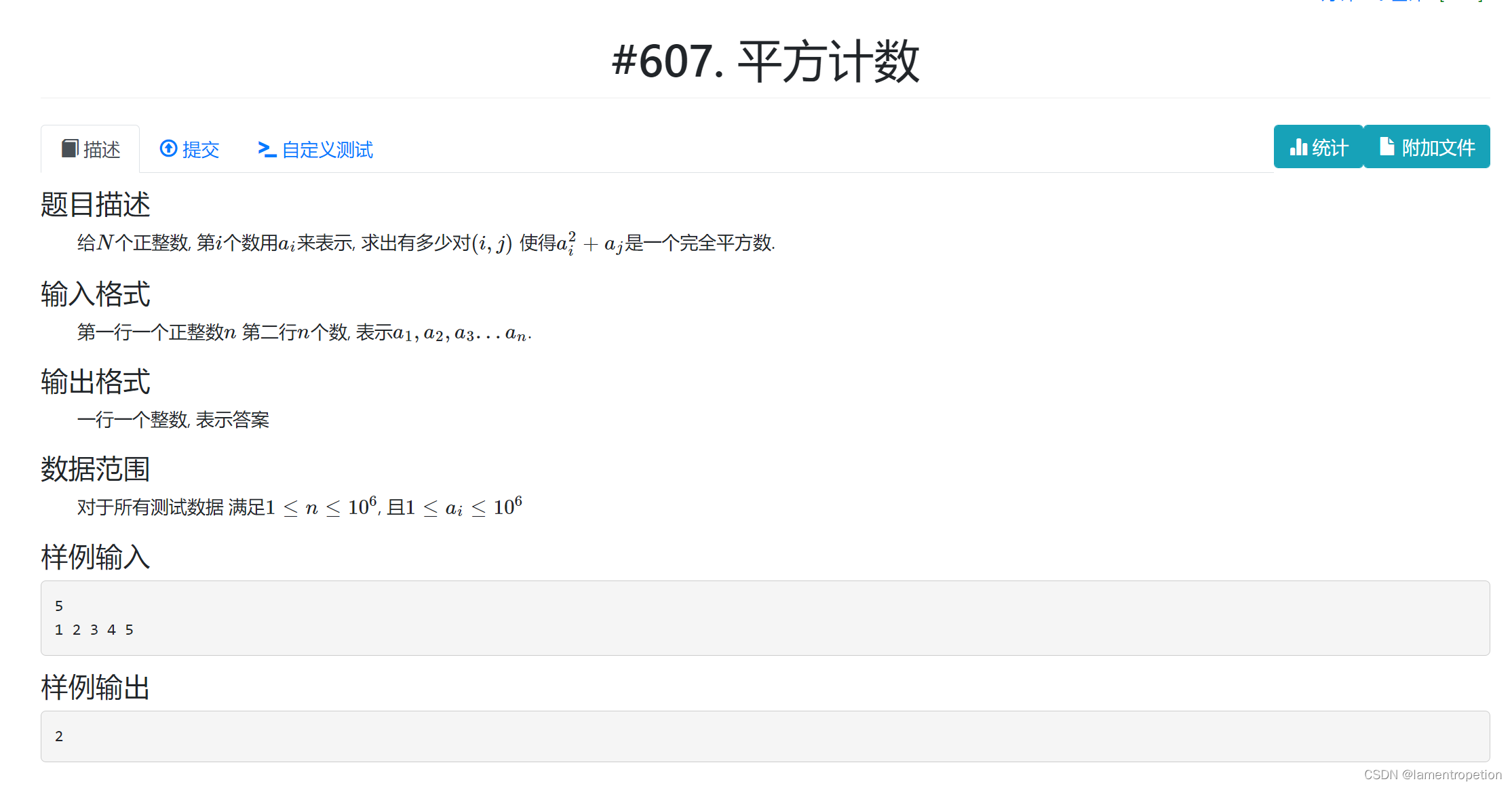
思路:
首先注意到暴力枚举一定超时,因此我们考虑只枚举一个指针,然后推一推式子降低另一个指针的复杂度
对于完全平方数这个条件,我们无法直接转换
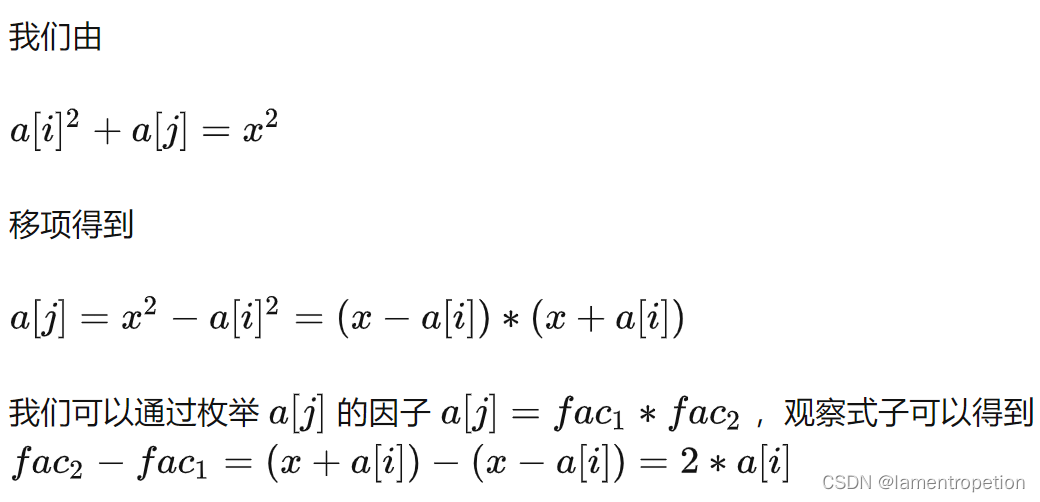
即对于每一个a[i],看是否存在a[j]使得a[j]有两个因子满足两个因子之差为2*a[i]
所以可以跑满1e6的所有数的因子,如果存在这样的数,就加上其贡献
Code:
#include <bits/stdc++.h>
using namespace std;
const int mxn=1e6+10;
int n,ans=0;
int a[mxn],mp[mxn];
int main(){
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
cin>>n;
for(int i=1;i<=n;i++) cin>>a[i],mp[a[i]]++;
for(int i=1;i<=1e6;i++){
for(int j=i;j<=1e6;j+=i){
int f1=max(i,j/i),f2=min(i,j/i);
int d=f1-f2;
if(d%2==0){
ans+=mp[d/2]*mp[j];
}
}
}
cout<<ans/2<<'\n';
}总结:
枚举超时:
1.如果是1e18,考虑打表找规律和logn算法
2.如果是枚举指针超时:
考虑枚举一个指针,然后推式子降低复杂度
或者更换枚举对象,枚举数据范围小的那个
对于无法直接转化的条件,可以推一推式子
当我们需要遍历一些数的因子时,可以枚举倍数预处理因子,复杂度为O(nlogn),降低复杂度