学习目标:
如果我要学习高等数学中的曲率,我会遵循以下步骤:
1.熟悉相关的数学概念:在学习曲率之前,我们需要了解曲线、切线和曲率半径等相关的数学概念。因此,我会复习这些概念,以便更好地理解曲率的概念和计算方法。
2.学习曲率的定义和公式:曲率是描述曲线在某一点的弯曲程度的量。它是曲线切线在该点处的曲率半径的倒数。因此,我会学习曲率的定义和计算公式,并通过例题和练习题进行实践和巩固。
3.理解曲率的性质和应用:曲率不仅是一种数学概念,也有广泛的应用。因此,我会理解曲率的性质和应用,包括曲率与曲线几何性质的关系、曲率在物理学、工程学和计算机图形学等领域的应用。
4.学习相关的数学工具:曲率涉及到微积分、向量和解析几何等多个数学分支。因此,我会学习相关的数学工具,以便更好地理解和应用曲率的概念和计算方法。
5.练习题和实践:最后,我会通过做一些练习题和实践,以巩固和加深我的理解和掌握曲率的知识和技能。
总之,学习高等数学中的曲率需要一定的数学基础和数学思维能力。我会通过理论学习和实践练习相结合的方式来学习曲率,并尽可能地将所学应用到实际问题中。

 我的理解:
我的理解:
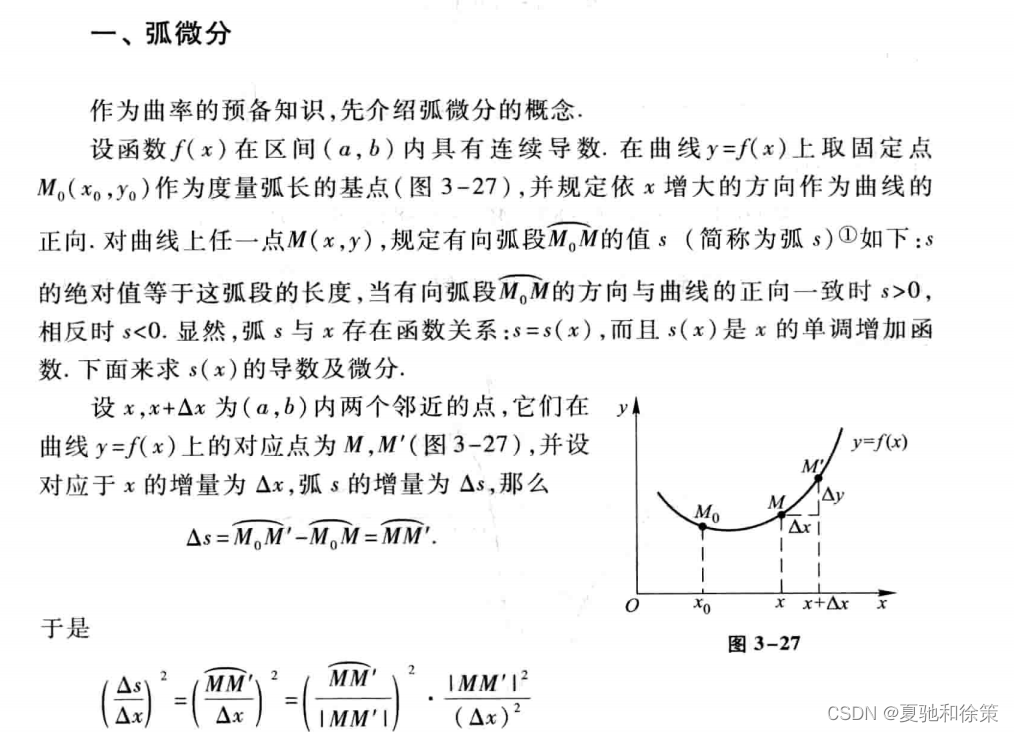
弧微分(Arc Length Differential)是曲线微积分中的一个重要概念,它表示曲线上相邻两点之间的距离微元。在实际应用中,弧微分可以用于计算曲线的长度、曲率和速度等。以下是弧微分的主要内容:
1.定义:弧微分表示曲线上相邻两点之间的距离微元。如果曲线的参数方程为 x = f(t) 和 y = g(t),则弧微分为 ds = sqrt[dx^2 + dy^2] = sqrt[(dx/dt)^2 + (dy/dt)^2] * dt。
2.计算长度:曲线的长度可以表示为从起点到终点的弧微分的累加。即 L = ∫ds = ∫sqrt[(dx/dt)^2 + (dy/dt)^2] * dt。
3.计算速度:速度是曲线上一点的切线方向上的瞬时速度。通过求弧微分的导数可以计算曲线上任意一点的速度,即 v = ds/dt = sqrt[(dx/dt)^2 + (dy/dt)^2]。
4.计算曲率:曲率表示曲线在某一点处的弯曲程度。通过求弧微分的二阶导数可以计算曲线在该点处的曲率,即 k = ds^2/d^2t = [d/dt(sqrt[(dx/dt)^2 + (dy/dt)^2])] / sqrt[(dx/dt)^2 + (dy/dt)^2]。
总之,弧微分是曲线微积分中的一个重要概念,它可以用于计算曲线的长度、曲率和速度等。在实际应用中,弧微分是非常有用的工具,可以帮助我们更好地理解和分析曲线的特性和行为。





我的理解:
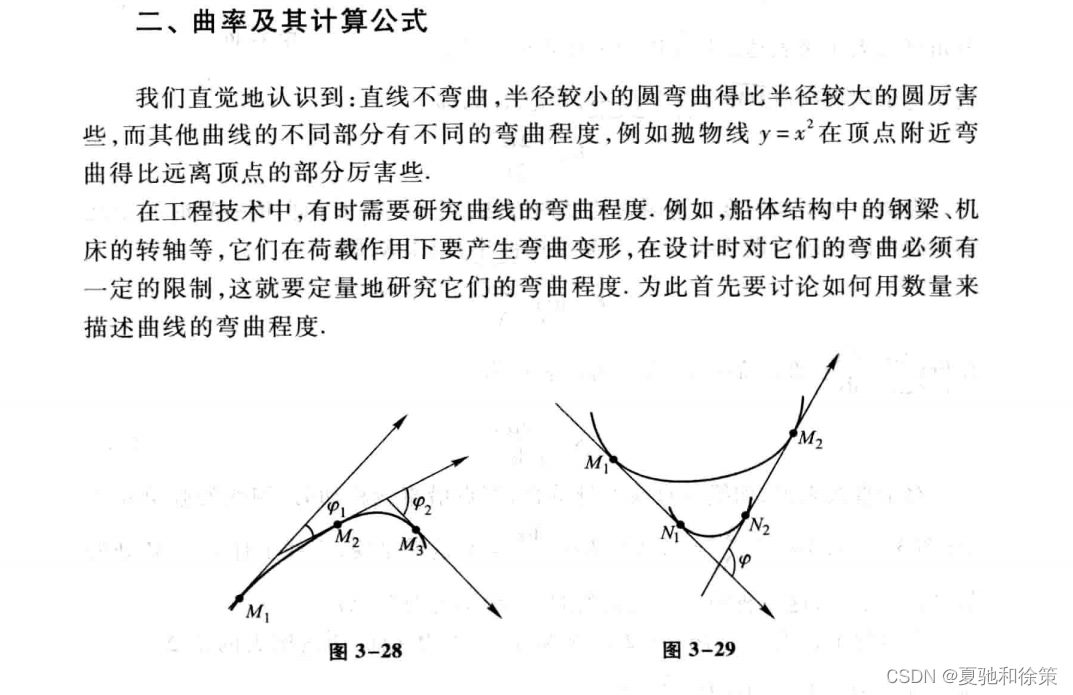
曲率(Curvature)是描述曲线在某一点处弯曲程度的量。在数学、物理学和工程学等领域中都有广泛的应用。以下是曲率及其计算公式的主要内容:
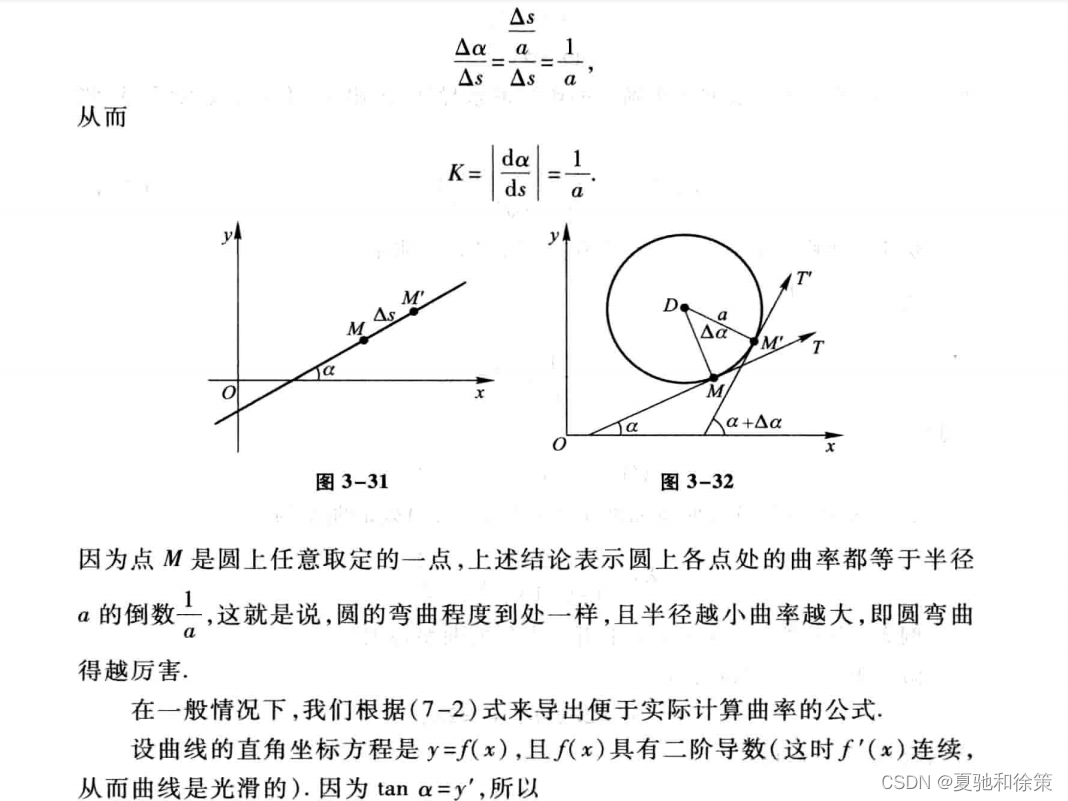
1.定义:曲率是指曲线在某一点处的弯曲程度,通常用曲线在该点处的曲率半径的倒数来表示。
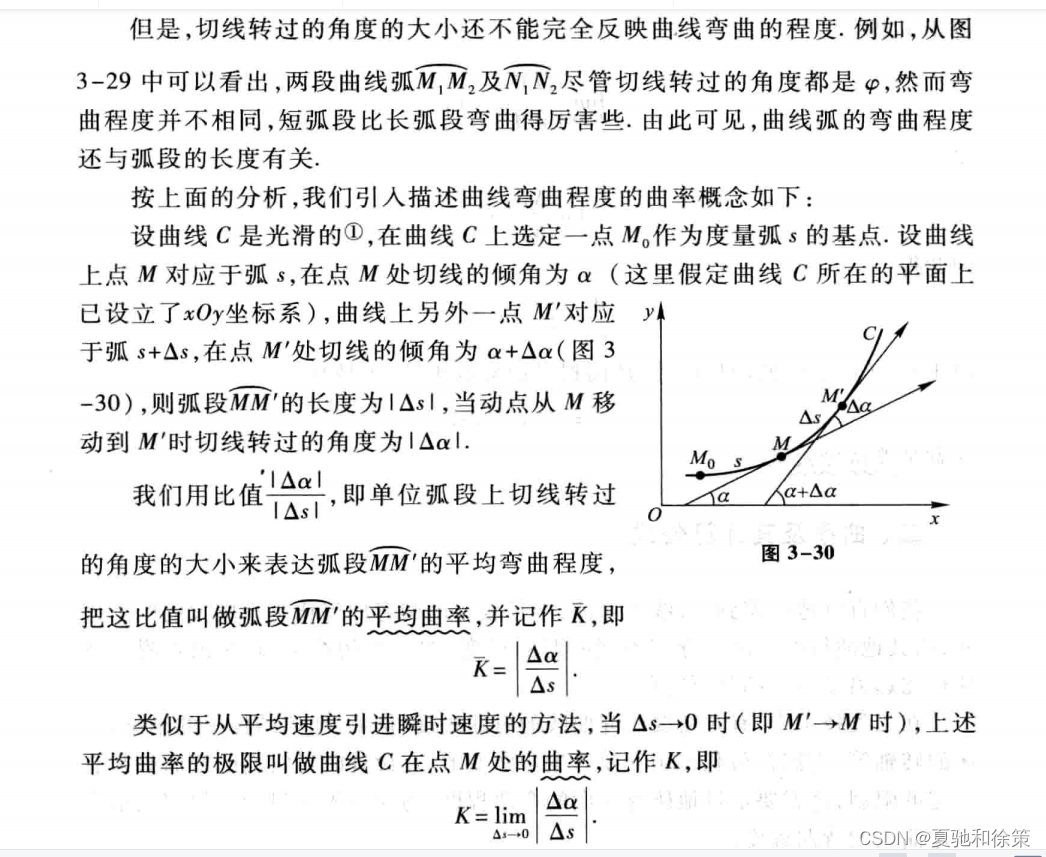
2.计算公式:设曲线的参数方程为 x = f(t),y = g(t),则曲率的计算公式为 k = |dθ/ds| = |d/ds (tanθ)|,其中 θ 为曲线在该点处的切线与 x 轴正方向之间的夹角,s 为曲线弧长。化简后,曲率的计算公式也可以表示为 k = |x'y'' - y'x''| / [(x'^2 + y'^2)^(3/2)],其中 x' = dx/ds,x'' = d^2x/ds^2,y' = dy/ds,y'' = d^2y/ds^2。
3.性质:曲率在曲线上不同点处的取值不同,可以用来描述曲线的几何特征,比如曲线的弯曲程度、拐角和尖锐程度等。在一些实际应用中,曲率也可以用于计算速度、加速度和转弯半径等。
总之,曲率是描述曲线在某一点处弯曲程度的量,可以用曲线在该点处的曲率半径的倒数来表示。曲率的计算公式可以通过曲线的参数方程和弧微分的概念来表示。曲率具有很多重要的几何性质和实际应用,对于理解和分析曲线的特性和行为非常有用。
 我的理解:
我的理解:
曲率圆和曲率半径是描述曲线在某一点处弯曲程度的另一种方式。它们与曲率的计算有着密切的关系。以下是曲率圆和曲率半径的主要内容:
1.定义:曲率圆是在曲线上某一点处与曲线切线相切,并且在该点处曲率与曲线相同的圆。曲率半径则是曲率圆的半径,通常用 R 来表示。
2.计算公式:曲率圆的计算可以通过曲率公式和切线方向来确定。具体来说,曲率圆的圆心坐标可以表示为 (x0, y0) = (x, y) + (1/k) * (-y', x'),其中 k 是曲率,x' 和 y' 分别是曲线在该点处的切线方向的 x 和 y 分量。曲率半径 R 则可以表示为 R = 1/k。
3.性质:曲率圆和曲率半径可以用于描述曲线在某一点处的弯曲程度。曲率半径越小,说明曲线在该点处的弯曲程度越大,曲线越陡峭。曲率圆和曲率半径也可以用于计算速度、加速度和转弯半径等。
总之,曲率圆和曲率半径是描述曲线在某一点处弯曲程度的一种方法。曲率圆是在曲线上某一点处与曲线切线相切,并且在该点处曲率与曲线相同的圆,曲率半径则是曲率圆的半径。曲率圆和曲率半径可以用于描述曲线的几何特征和计算曲线的物理量。在实际应用中,曲率圆和曲率半径也是非常有用的工具。

我的理解:
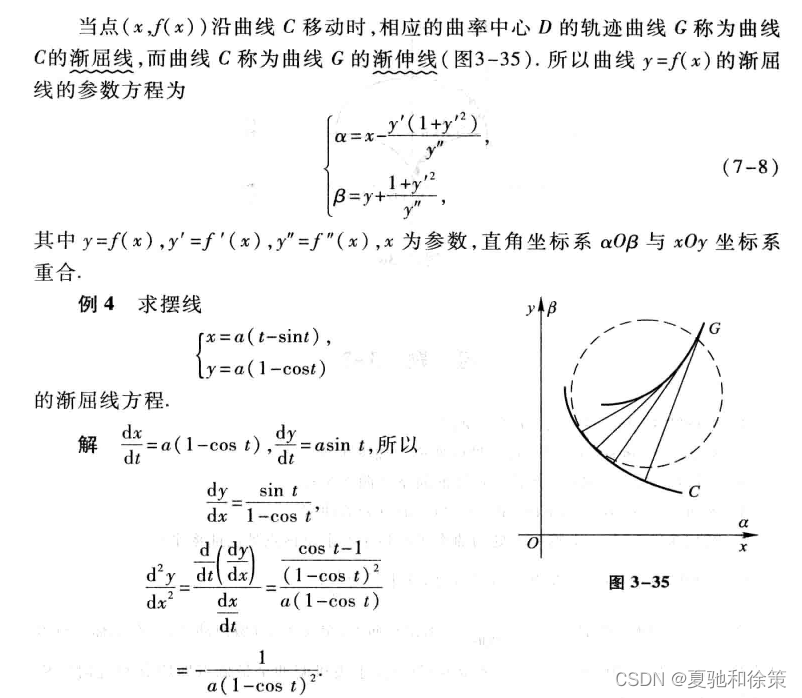
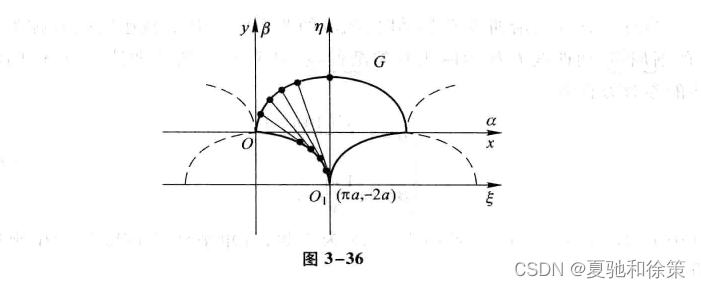
曲率中心是描述曲线弯曲特性的一个重要参数,用于确定曲线在某一点处的曲率圆的位置。以下是曲率中心、渐屈线和渐伸线的主要内容:
1.曲率中心:曲率中心是曲线在某一点处的曲率圆所在的位置。曲率中心通常用 (x_c, y_c) 来表示,可以通过曲线的二阶曲率和切线方向来计算。具体计算公式为 x_c = x + (1/k') * (-y''/((1+y'²)^(3/2))), y_c = y + (1/k') * (x''/((1+y'²)^(3/2))),其中 k' 是二阶曲率。
2.渐屈线和渐伸线:渐屈线和渐伸线是曲线在某一点处切线的两个方向。渐屈线方向是曲线弯曲程度最大的方向,它与曲线在该点处的曲率圆相切。渐伸线方向则是曲线在该点处最陡峭的方向,与曲线在该点处的曲率圆相切,并且与渐屈线垂直。
3.计算公式:渐屈线和渐伸线的计算可以通过曲线的切线方向和曲率半径来确定。具体来说,渐屈线方向的单位向量为 (cosθ, sinθ),其中 θ 是切线方向与水平方向的夹角,可以通过曲线在该点处的曲率半径 R 和切线方向计算得到。渐伸线方向的单位向量则是渐屈线方向的垂直向量,即 (-sinθ, cosθ)。
总之,曲率中心、渐屈线和渐伸线是描述曲线弯曲特性的重要参数。曲率中心是曲线在某一点处的曲率圆所在的位置,可以通过曲线的二阶曲率和切线方向计算得到。渐屈线和渐伸线是曲线在某一点处切线的两个方向,可以通过曲率半径和切线方向计算得到。在实际应用中,曲率中心、渐屈线和渐伸线是非常有用的工具,可用于计算转弯半径、车辆行驶路径规划等。