435. 无重叠区间

和452. 用最少数量的箭引爆气球 思路是很相似的。本题按照左边排序或者按照右边排序都是可以的，最终目的都是为了让区间尽可能重叠。
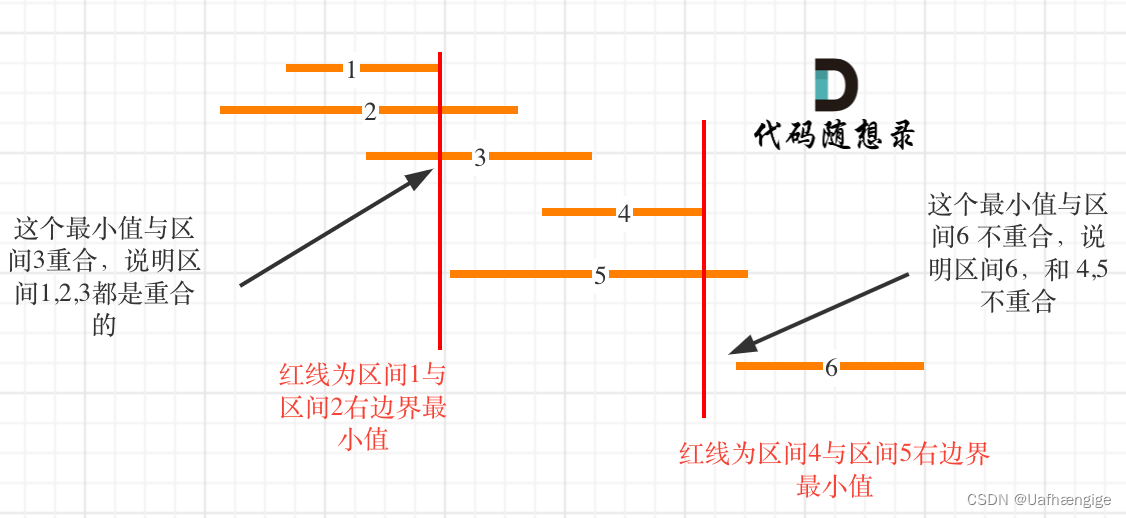
1、按右边排序，排序完第一个元素的右边界一定是最小右边界。往下找第一个不与其重合的左边界，找的话count+1。在找到4之前，1 2 3中最小右边界（最不容易与后面左边界重合的值，一定是1的右边界）

class Solution {
public:
    static bool cmp(const vector<int>& v1,const vector<int>& v2){
        return v1[1] < v2[1];
    }
    int eraseOverlapIntervals(vector<vector<int>>& intervals) {
        sort(intervals.begin(),intervals.end(),cmp);
        int count = 1;
        int end = intervals[0][1];
        for(int i = 1; i < intervals.size(); ++i){
            if(intervals[i][0] >= end){
                count++;
                end = intervals[i][1];
            }
        }
        return intervals.size() - count;
    }
};

2、按左边界排序。
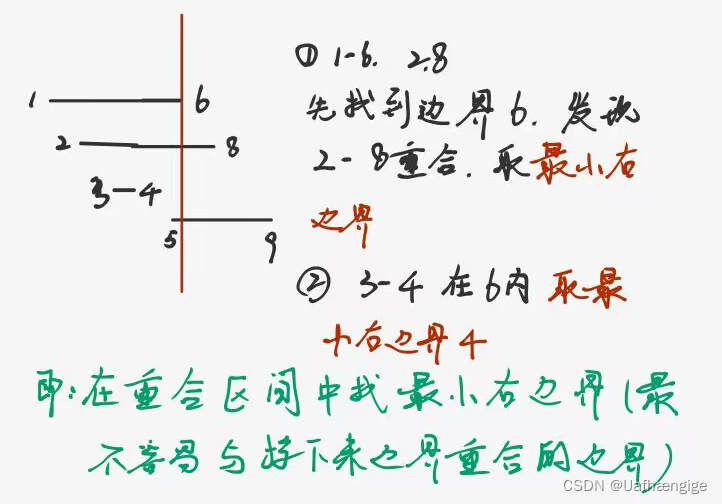
根据右边界排序，一下子就能找到下一个不重合的区域是4。但是按照左边界的排序，找的是重合区域。

class Solution {
public:
    static bool cmp(const vector<int>& v1,const vector<int>& v2){
        return v1[0] < v2[0];
    }
    int eraseOverlapIntervals(vector<vector<int>>& intervals) {
        sort(intervals.begin(),intervals.end(),cmp);
        int count = 0;
        int end = intervals[0][1];
        for(int i = 1; i < intervals.size(); ++i){
            if(intervals[i][0] < end){
                count++;
                end = min(end,intervals[i][1]);
            }
            else{
                end = intervals[i][1];
            }
        }
        return count;
    }
};

763.划分字母区间

之前做过，直接能想到方法。但是！要注意更新maxindex要在收获结果之前！因为要设置maxindex的初始值。如果是INT_MIN，但是cdaa这种情况，先收获结果的话，就会漏掉index = 0，c单独分割的情况。

class Solution {
public:
    vector<int> partitionLabels(string s) {
        vector<int> res;
        unordered_map<char, int> map;
        int maxIndex = INT_MIN;
        for (int i = 0; i < s.size(); ++i) {
            map[s[i]] = i;
        }
        for(int i = 0; i < s.size(); ++i){
            if(map[s[i]] > maxIndex) maxIndex = map[s[i]];
            if(i == maxIndex){
                int sum = 0;
                for(int a : res) sum += a;
                int temp = i + 1 - sum;
                res.push_back(temp);
                
            }
        }
        return res;
    }
};

56. 合并区间

和452. 用最少数量的箭引爆气球 (opens new window) 和 435. 无重叠区间 (opens new window) 都是一个套路。
卡哥直接在res数组里融合区间，更简洁一些

result.back()[1] = max(result.back()[1], intervals[i][1]); 

自己的方式是通过left和right来记录重叠区间

class Solution {
public:
    static bool cmp(const vector<int>& v1, const vector<int>& v2){
        return v1[0] < v2[0];
    }
    vector<vector<int>> merge(vector<vector<int>>& intervals) {
        vector<vector<int>> res;
        sort(intervals.begin(),intervals.end(),cmp);
        int left = intervals[0][0];
        int right = intervals[0][1];
        for(int i = 1; i < intervals.size(); ++i){
            if(intervals[i][0] <= right){
                right = max(right,intervals[i][1]);
            }
            else{
                vector<int> vec;
                vec.push_back(left);
                vec.push_back(right);
                res.push_back(vec);
                left = intervals[i][0];
                right = intervals[i][1];
            }
        }
        vector<int> vec;
        vec.push_back(left);
        vec.push_back(right);
        res.push_back(vec);
        return res;
    }
};

738.单调递增的数字

本质是从后向前遍历，到第一个满足升序的位置，减一，然后后面的数置为9。比如322变成299。但是在处理方式上，如果遇到100，用数组处理就很非常麻烦，会遇到位数缩减的问题。**string有一个函数stoi，可以将string转换成int。**会自动去除无效位数。所以可以将数字先通过to_string转成字符串处理。处理完以后再转为int

class Solution {
public:
    int monotoneIncreasingDigits(int n) {
        string str = to_string(n);
        int index = str.size();
        for(int i = str.size() - 1; i > 0; --i){
            if(str[i] < str[i-1]){
                index = i;
                str[i-1]--;
            }
        }
        for(int i = index; i < str.size(); ++i){
            str[i] = '9';
        }
        return stoi(str);
    }
};

968.监控二叉树

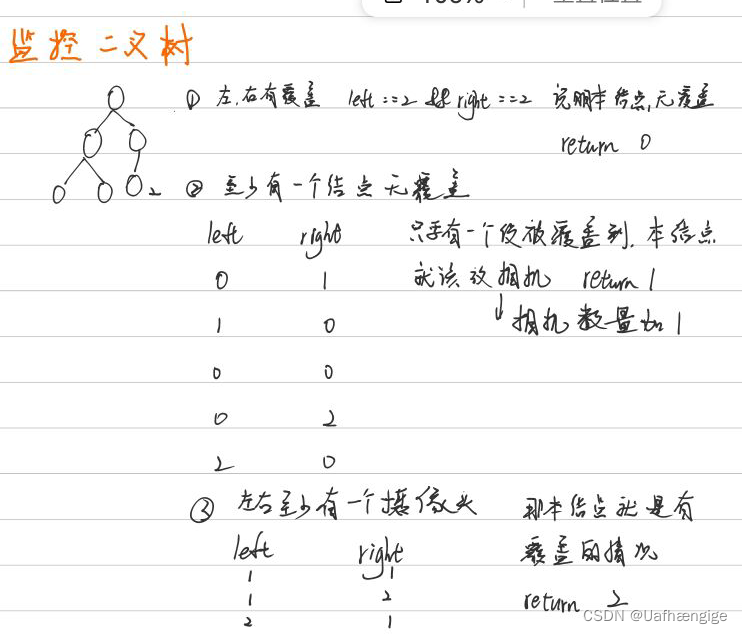
想到了后序遍历，也想到子节点的父节点给摄像头。但是考虑并不周全。本题可以使用状态转移。
一个节点可能处于三种情况下：
1、没覆盖：0
2、有相机：1
3、有覆盖：2

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int count = 0;
    int minCameraCover(TreeNode* root) {
        if(find(root) == 0){
            count++;
        }
        return count;
    }
    int find(TreeNode* cur){
        if(cur == nullptr) return 2;
        int left = find(cur->left);
        int right = find(cur->right);
        if(left == 2 && right == 2) return 0;
        if(left == 0 || right == 0) {
            count++;
            return 1;
        }
        if(left == 1 || right == 1) return 2;
        return -1;
    }
};