2022年第十三届蓝桥杯题解（全）C/C++

A题就是一个简单的进制转化，代码实现如下：

#include <bits/stdc++.h>

using namespace std;

const int N = 1e5 + 10;

int main()
{
	int x = 2022;
	int a = 1;
	int res = 0;
	while(x) {
		res += (x % 10) * a;
		a = a * 9;
		x /= 10;
	}
	cout << res;
	
	return 0;
}

B题有很大的争议，我认为顺子的意思是从0开始的至少为三个数的升序序列。那这样的话答案就是：14

C题是一个很普通的思维题，先记录一下每周能做多少题，然后统计一下总的做题数除以每周能做的题然后乘以7，再加上从周一开始计算每一天什么时候能大于这个总的题数的天数即可。

#include <bits/stdc++.h>

using namespace std;
typedef long long LL;

const int N = 1e5 + 10;

int main()
{
	LL a, b, n, t, res;
	cin >> a >> b >> n;
	
	t = a * 5 + b * 2;
	res = n / t * 7;

	n %= t;
	if(n > 0)
		for(int i = 1; i <= 7; i ++ )
		{
			if(i == 6 || i == 7) n -= b;
			else n -= a;
			res ++;
			if(n <= 0) break;
		}
	
	cout << res;
	
	return 0;
}

D题应该是最简单的一道，开一个n的数组a[i]，a[i]表示每一个灌木能长得最大高度，最大高度等于它右侧的树木数乘以2；

#include <bits/stdc++.h>

using namespace std;
typedef long long LL;

const int N = 1e4 + 10;

int a[N], n;

int main()
{
	cin >> n;
	for(int i = 1; i <= (n + 1) / 2; i ++ ) {
		a[i] = (n - i) * 2;
		a[n - i + 1] = a[i];
	}
	
	for(int i = 1; i <= n; i ++ ) {
		cout << a[i];
		if(i != n) cout << "\n";
	}
	
	return 0;
}

E题就开始有点意思了，这道题是一个简单贪心，重点在于读题（其实接触过这个进制问题的童鞋应该一样就看懂了emmm）。

我们先分析一下题干的65是怎么出来的：第一数位每一个数代表的必然是1，第二数位是由第一数位的二进制晋上来的，所以第二数位每一个数代表的是2，第三数位是由第二数位十进制进位上来的，所以第三数位每一个数代表的是2 * 10 = 20，所以这个x(321) = 3 * 20 + 2 * 2 + 1 * 1 = 65;

题目的意思是保证x(a) >= x(b) , 求两个数的差值最小。显然对于每一数位，其进制越小，两个数的后一数位做差所得到的值越小，所以每一数位最小的合法进制数就行。

#include <bits/stdc++.h>
#define int long long

using namespace std;

const int mod = 1e9 + 7, N = 1e5 + 10;

int a[N], b[N];
int ma, mb, n;

signed main()
{
	cin >> n;
	cin >> ma;
	for(int i = 1; i <= ma; i ++ ) cin >> a[i];
	for(int i = 1; i <= ma / 2; i ++ ) swap(a[i], a[ma - i + 1]);
	
	cin >> mb;
	for(int i = 1; i <= mb; i ++ ) cin >> b[i];
	for(int i = 1; i <= mb / 2; i ++ ) swap(b[i], b[mb - i + 1]); 
	
	int t = 1, ans = 0;
	//枚举每个数位
	for(int i = 1; i <= ma; i ++ ) {
		//当前数位贪心最优的进制 
		int z = max(a[i], b[i]) + 1;
		if(z < 2) z = 2; 
		ans += a[i] * t - b[i] * t;
		ans %= mod;
		t = t * z % mod;
	}
	
	cout << ans;
	
	return 0;
}

F题可以暴力写一下,求一个前缀和，然后枚举子矩阵，时间复杂度是O(n^4)，显然过不了；

这个题考的是一个双指针，枚举一下矩阵中的左右边界，在每一个左右边界中，从上往下求一下子段中小于等于k的数的数量（用双指针扫一下就可以，这一步可以做到o(n)）;

时间复杂度：O(n ^ 3)

#pragma GCC optimize(2)
#pragma GCC optimize(3)
#pragma GCC optimize(fast)
#include <bits/stdc++.h>

using namespace std;

const int N = 510;
typedef long long LL;

int a[N][N];

int main()
{
    int n, m, k;
    scanf("%d%d%d", &n, &m, &k);
    
    for(int i = 1; i <= n; i ++ )
        for(int j = 1; j <= m; j ++ )
            scanf("%d", &a[i][j]);
            
    for(int i = 1; i <= n; i ++ )
        for(int j = 1; j <= m; j ++ )
            a[i][j] += a[i][j - 1];
    
    LL cnt = 0;
    for(int i = 1; i <= m; i ++ )
        for(int j = i; j <= m; j ++ ) {
            int res = 0;
            for(int l = 1, r = 1; r <= n; r ++ ) {
                res += a[r][j] - a[r][i - 1];
                while(res > k && l <= r) {
                    res -= a[l][j] - a[l][i - 1];
                    l ++;
                }
                if(res <= k && l <= r) cnt += r - l + 1;
            } 
        }
    printf("%lld", cnt);
    
    
    return 0;
}

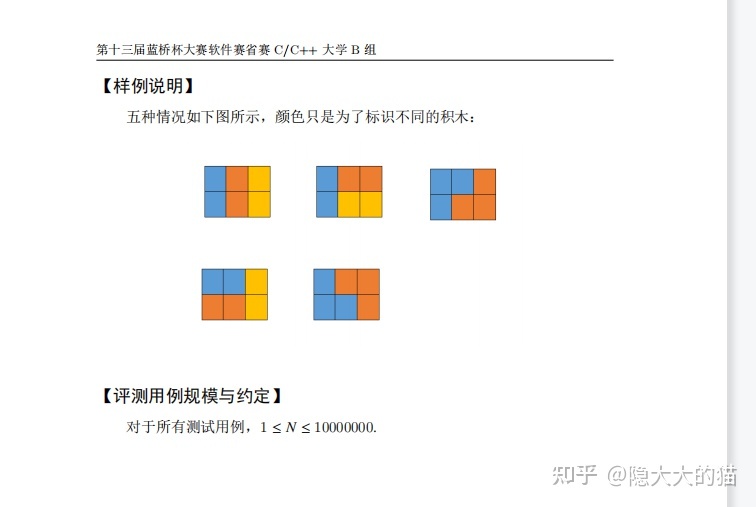
这个题考的是一个dp;

状态表示: f[i][j]表示前i列积木中，第i列状态为j的情况数。

四种情况:j = 0, 表示当前列为空， 1表示当前列上面有一个格子，2表示当前列下面有一个格子，3表示当前列已满。

由于数据很大，开一个4e8的空间会爆，可以用p来表示上一层状态，q来表示当前层的状态，类似于背包的滚动数组优化。

状态转移看一下代码吧，我感觉还是比较好理解的，不懂的可以评论区问我

#include <bits/stdc++.h>

using namespace std;
typedef long long LL; 

const int N = 1e7 + 10, mod = 1e9 + 7;

LL p[4], q[4];

int main()
{
	int n;
	cin >> n;
	
	p[3] = 1;
	for(int i = 1; i <= n; i ++ ) {
		q[3] = (p[0] + p[1] + p[2] + p[3]) % mod;
		q[0] = p[3] % mod;
		q[1] = (p[0] + p[2]) % mod;
		q[2] = (p[0] + p[1]) % mod;
		for(int i = 0; i <= 3; i ++ )
		    p[i] = q[i];
	}
	cout << p[3];
	return 0;
}

ps:题不可以用并查集去做，因为雷的爆炸是由方向的，A雷爆炸可以引爆B雷，但是B雷爆炸是有可能无法引爆B雷的（爆炸半径不同）

ps:我补题的时候被卡常卡了一天，最后把idx.find改成idx.count就过了（emm55555）

正解是dfs，为了避免边被卡成O(n * n), 以至于tle，我们就需要去除重复的点，记录每一个坐标下点的位置.

然后把每一个火箭作为根节点，去遍历周围r ^ 2的雷，统计一下一共能炸多少雷就可以。

O(100 * n + m）最坏情况为每一个雷有100条边；

#pragma GCC optimize(2)
#include <bits/stdc++.h>

using namespace std;
typedef long long LL;

const int N = 2e5 + 10;

struct Node {
    int x, y, r, l;
}a[N];
//x，y到下标的映射
unordered_map<LL, int> idx;
bool st[N];
int n, m, cnt;
int ans;

LL cal(int x, int y) {
    return (LL)x * (1000000000 + 1) + y;
}

bool solve(int x, int y, int r) {
    if(x * x + y * y <= r * r) return true;
    else return false;
}

void dfs(int i)
{
    //标记当前点
    st[i] = true;
    //加上当前点雷的数量
    ans += a[i].l;
    int r = a[i].r;
    //printf("%d %d %d\n", a[i].x, a[i].y, a[i].r);
    //遍历当前点周围是否有没遍历的子节点，有的话继续dfs
    for(int x = max(a[i].x - r, 0); x <= min(a[i].x + r, 1000000000); x ++ ) {
        for(int y = max(a[i].y - r, 0); y <= min(a[i].y + r, 1000000000); y ++ ) {
            if(solve(x - a[i].x, y - a[i].y, r)) {
                LL xy = cal(x, y);
                if(idx.count(xy)) {
                    int u = idx[xy];
                    if(!st[u]) {
                        dfs(u);
                        //printf("%d\n", u);
                    }
                }
            }
        }
    }
    
}

int main()
{
    scanf("%d%d", &n, &m);
    
    for(int i = 1; i <= n; i ++ ) {
        int x, y, r;
        scanf("%d%d%d", &x, &y, &r);
        LL xy = cal(x, y);
        //如果没有这个点
        if(idx.find(xy) == idx.end()) {
            //将这个点存入idx数组
            idx[xy] = ++cnt; 
            //将这个点存入a数组
            a[cnt] = {x, y, r, 1};
        }
        else {
            int u = idx[xy];
            //这个点已经存在并且半径更大，则会更新这个以前点的编号下的r的值
            a[u].r = max(a[u].r, r);
            //这个点的出现次数加一
            ++ a[u].l;
        }
        //int u = idx[xy];
        //printf("%d %d %d %d\n", a[u].x, a[u].y, a[u].r, a[u].l);
    }
    for(int i = 1; i <= m; i ++ ) {
        int x, y, r;
        scanf("%d%d%d", &x, &y, &r);
        //将这个点加入a中作为起始点，去搜一下其他的雷
        a[cnt + 1] = {x, y, r};
        dfs(cnt + 1);
    }
    printf("%d", ans);
    
    return 0;
}

I题又是一个dp，这个dp感觉比上面那个简单一点；

状态表示：f[i][j][k]表示访问前i个位置时，恰好访问j个店并且酒量恰好为k的时候的方案数；

准确来说这个做法并不能维护所有前i个位置恰好访问j个店的方案数，但是题目只问最后一次遇到花且恰好把酒喝光的次数，所以对于大于100的酒量的状态就不用转移了，因为在后面接近100个位置中，全看花也不能把酒喝完。

状态转移; 看花： f[i][j][k] = f[i - 1][j][k + 1] 遇店： f[i][j][k] = f[i - 1][j - 1][k / 2];//注意边界！不要越界

#include <bits/stdc++.h>

using namespace std;

const int N = 110, mod = 1e9 + 7;

//前i次访问，访问j个店的酒量是多少
long long f[N * 2][N][110];

int main()
{
    int n, m;
    scanf("%d%d", &n, &m);
    
    f[0][0][2] = 1;
    for(int i = 1; i < n + m; i ++ )
        for(int j = 0; j <= n; j ++ )
            for(int k = 0; k <= 100; k ++ ) {
                f[i][j][k] = (f[i][j][k] + f[i - 1][j][k + 1]) % mod;
                if((k % 2 == 0) && j) f[i][j][k] = (f[i][j][k] + f[i - 1][j - 1][k / 2]) % mod;
            }
    printf("%lld", f[n + m - 1][n][1]);
    
    return 0;
}

这个题有两个做法，一种是用set或者堆来维护一个高度到区间的映射，另一个用并查集维护区间，这个做法我没做出来，我用了两个set来做，果然被卡常了.

正解：这个题本质是一个最长公共下降子序列的问题，对于任意一个h,只要它高度降到了与前一个高度下降过程中的公共值，那么它就不需要花费代价继续下降。如果它降得的当前高度与前一个高度没有公共值，则需要多花费一个代价，来降低自己的高度。我们只需要开两个数组暴力做一下就行。

时间复杂度: O(n);

#include <bits/stdc++.h>

using namespace std;
typedef long long LL;

const int N = 2e5 + 10;

LL a[N];
vector<LL> b[N];
int n;

LL solve(LL x) {
    return sqrt(x / 2 + 1);
}

int main() {
    scanf("%d", &n);

    for(int i = 1; i <= n; i ++ ) scanf("%lld", &a[i]);

    int res = 0;

    for(int i = 1; i <= n; i ++ ) {
        while(a[i] > 1) {
            int flag = 0;
            for(LL j : b[i - 1]) {
                if(a[i] == j) {
                    flag = 1;
                    break;
                }
            }
            if(!flag) res ++;
            b[i].push_back(a[i]);
            a[i] = solve(a[i]);
        }

    }
    printf("%d", res);

    return 0;
}