个人主页:平行线也会相交
欢迎 点赞👍 收藏✨ 留言✉ 加关注💓本文由 平行线也会相交 原创
收录于专栏【数据结构初阶(C实现)】
本篇主要讲解八大排序算法中的三种排序,分别是:插入排序、希尔排序、选择排序。
目录
- 插入排序
- 插入排序代码
- 希尔排序
- 希尔排序的时间复杂度
- 希尔排序总代码
- 选择排序
- 直接选择排序代码
- 直接选择排序时间复杂度及总结
插入排序
在我们的日常生活最常见的一个场景就是斗地主,我们在斗地主摸牌的过程中其实就是利用插入排序来整理我们摸到的牌,按照从大到小或者从小到大的进行比较,大的放左边或者小的放左边。斗地主摸牌流程是这样的:最初我们拿到第一张牌的时候,我们把这一张牌当成一个有序序列,当我们拿到第二张牌的时候,我们用第二张牌和有序序列进行一一的比较,大的放右边,小的放左边(这里按照升序进行排序),排完第二张牌之后,此时有序序列就变成了两张牌,再用拿到的第三张牌与有序序列进行比较,依次类推,直到排完我们拿到的所有牌。(所以我们摸牌的过程就是一个插入排序)
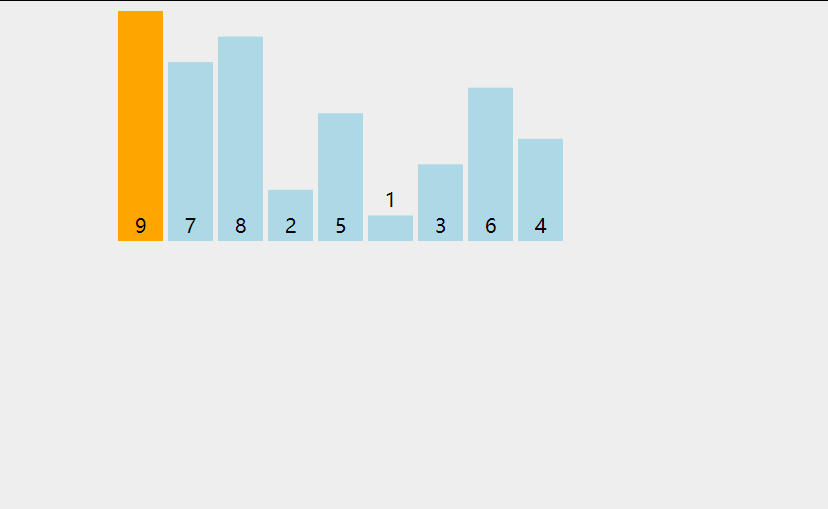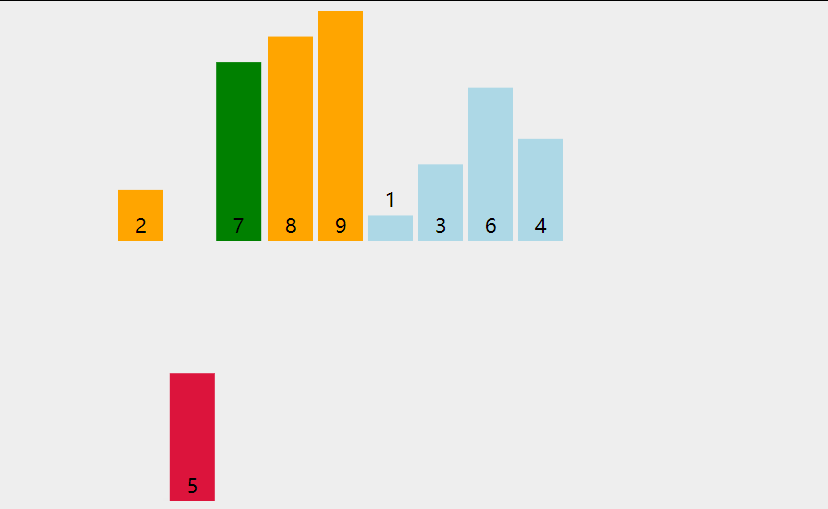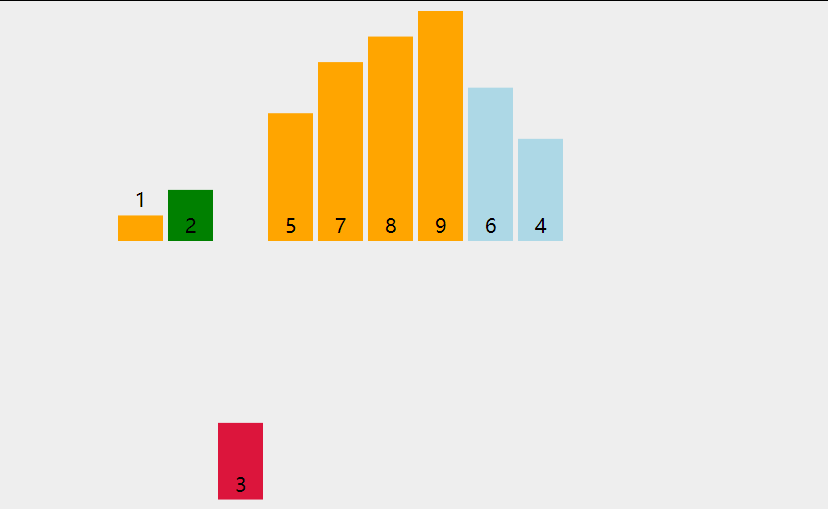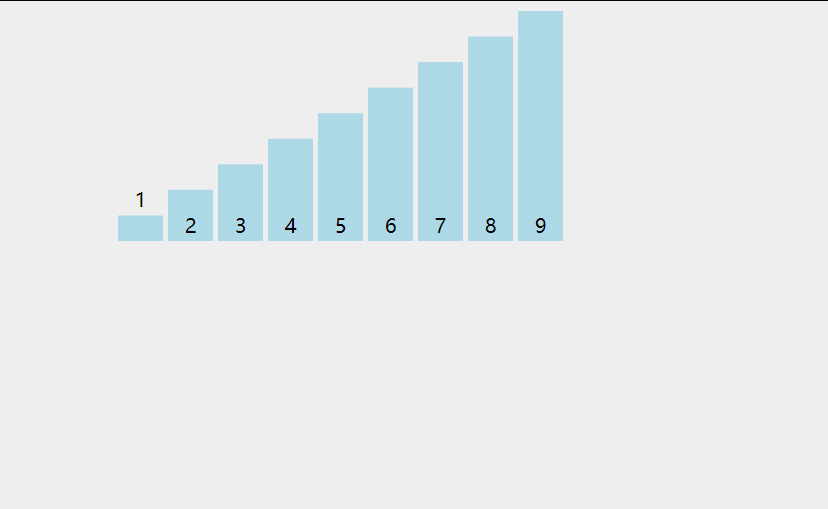
上图就是插入排序的动态演示图。
插入排序思想:把待排序的记录按照其关键码值的大小逐个插入到一个排序好的有序序列中,直到所有的记录插入完为止,最后得到一个新的序列。
下面来正式看插入排序的内容:
直接插入排序的特性:
1.元素集合越接近有序,直接插入排序的算法的时间效率复杂度越高。
2.时间复杂度:O(N^2),最坏的情况就是序列是一个倒序。
3.空间复杂度O(1)。
插入排序代码
#include<stdio.h>
#include<stdlib.h>
void PrintArray(int* a, int n)
{
for (int i = 0; i < n; i++)
{
printf("%d ", a[i]);
}
}
//插入排序
void InsertSort(int* a, int n)
{
for (int i = 1; i < n; i++)
{
int end = i - 1;//有序的个数
int tmp = a[i];
while (end >= 0)
{
if (tmp < a[end])
{
a[end + 1] = a[end];
end--;
}
else
{
break;
}
}
a[end + 1] = tmp;
}
}
int main()
{
int a[10] = { 9,1,5,3,7,6,8,2,4,10 };
InsertSort(a, sizeof(a) / sizeof(a[0]));//插入排序
PrintArray(a, sizeof(a) / sizeof(a[0]));
return 0;
}

希尔排序
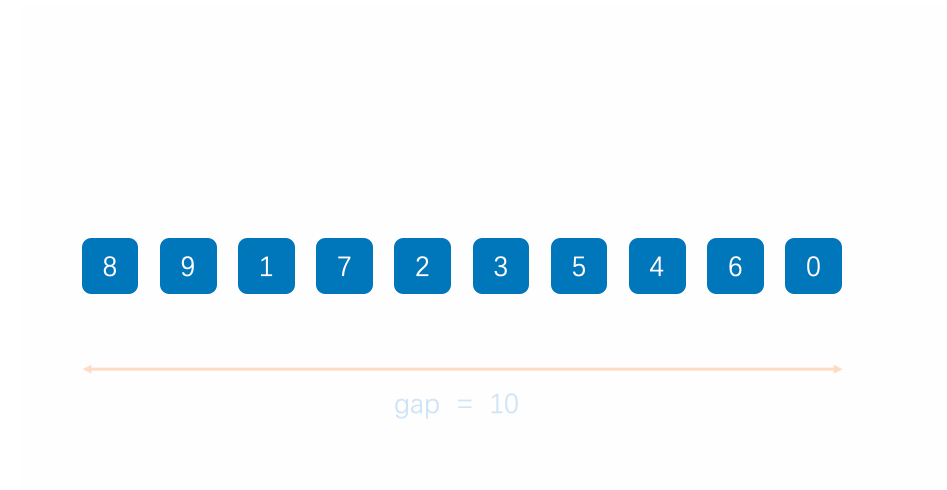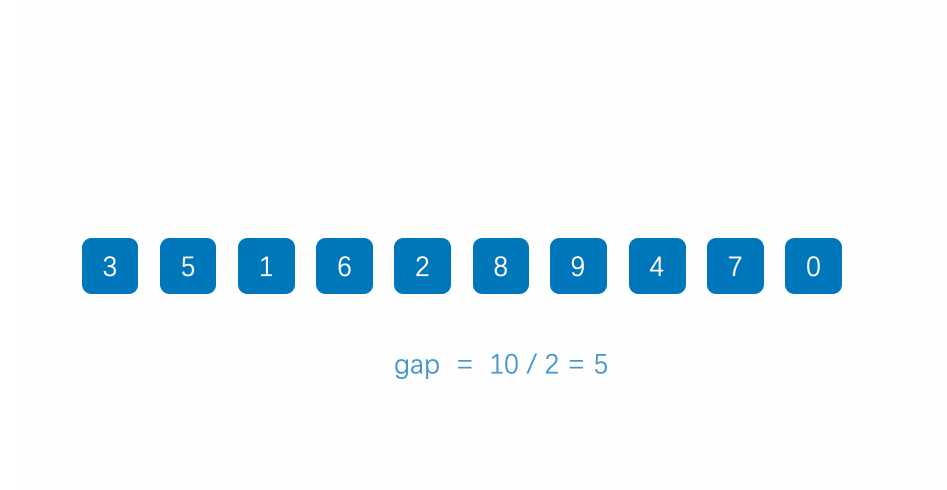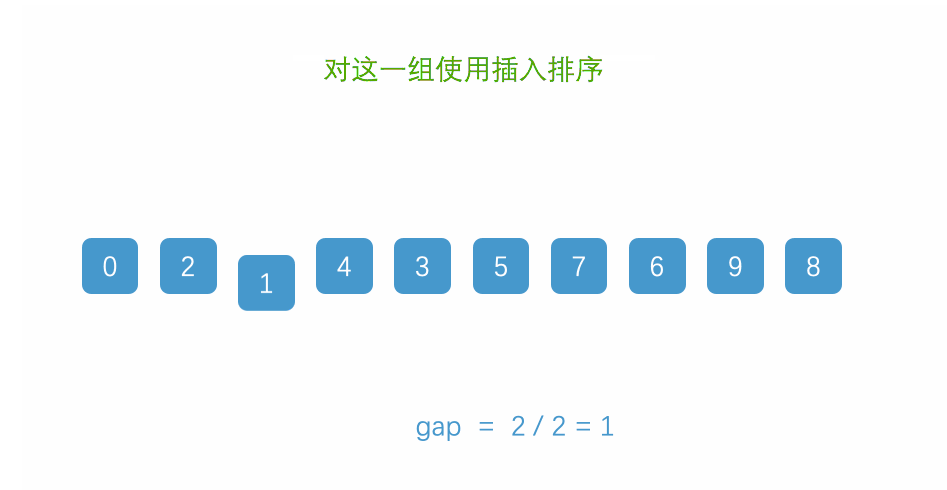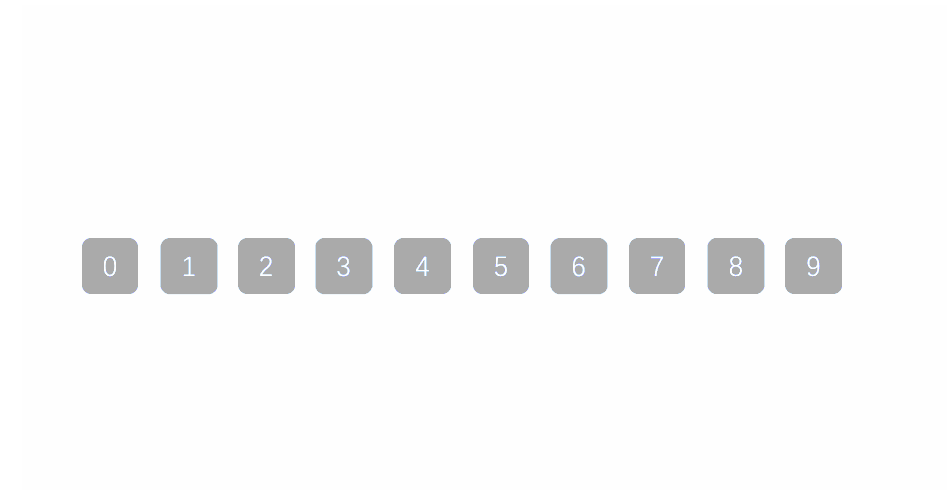
首先,整个希尔排序就分为两个步骤:先进行预排序,然后进行插入排序。
我们知道,插入排序算法中如果序列本身已经很接近有序了,那么插入排序是一个不算的算法,那如果序列本身离着有序还很远,此时如果再用插入排序算法的话,效率就会非常低。所以这就引出了希尔排序(对插入排序进行优化)。
希尔排序首先要对序列进行预排序,即分组插入进行排序(间隔为gap的分为一组,gap是几序列就会被分为几组),然后对每组数据进行插入排序。也就是说我们需要进行gap组插入排序。
如下图:
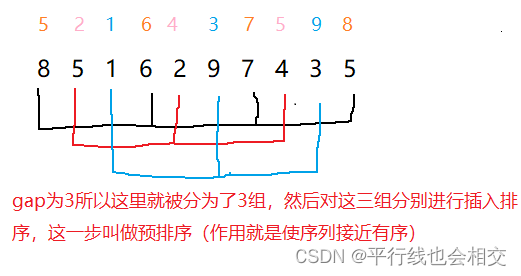
关于预排序这一步,有两种处理方法:一种是一组排完再排另外一组;另一种方法就是多组并排。(代码的话就到最后一同罗列出来把)
第二步就是对序列进行最后的排序。
比如说:我们先以gap=3为间隔进行预排序,最后再调用InsertSort插入函数进行最后的排序。代码就是这样的,请看:
void ShellSort(int* a, int n)
{
int gap = 3;
//一组排完再排另一组
for (int j = 0; j < gap; j++)
{
for (int i = gap + j; i < n; i += gap)
{
int end = i - gap;;
int tmp = a[i];
while (end >= 0)
{
if (tmp < a[end])
{
a[end + gap] = a[end];
end -= gap;
}
else
{
break;
}
}
a[end + gap] = tmp;
}
}
for (int k = 0; k < n; k++)
{
printf("%d ", a[k]);
}
printf("\n");
InsertSort(a, n);
}
上述的先进行预排序,然后进行最终的排序算是一种解决方法。但如果我们要排序的是一亿个数呢?我们不可能再像上述那样把gap设置为3。而是对gap进行一个动态的调控,即gap是随着我们不断地对数据进行排序而发生变化。就像下图那样,请看:
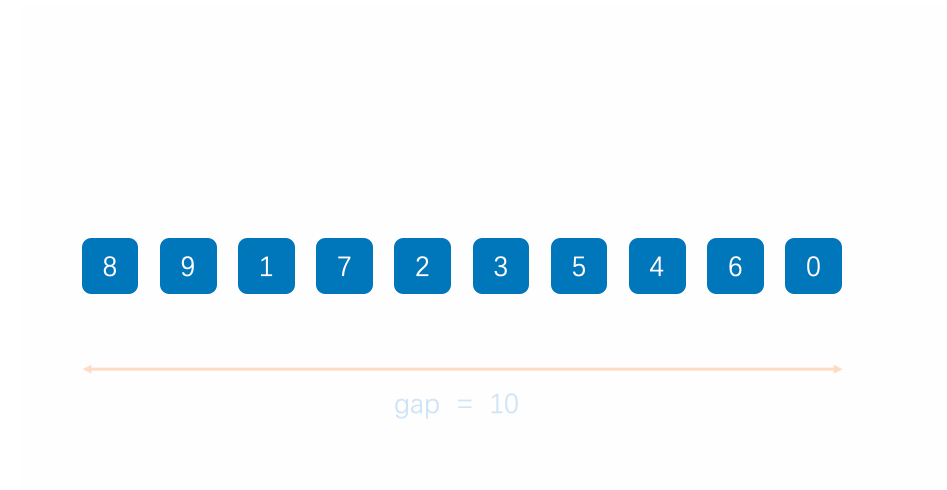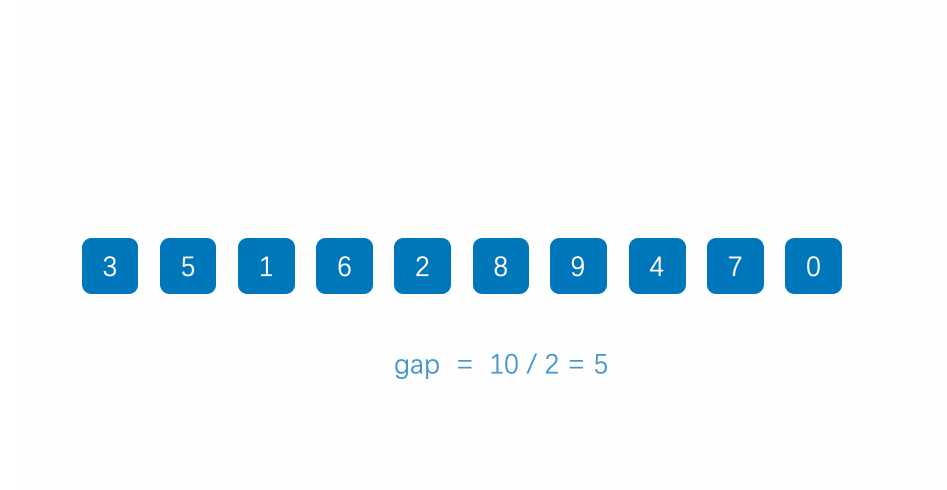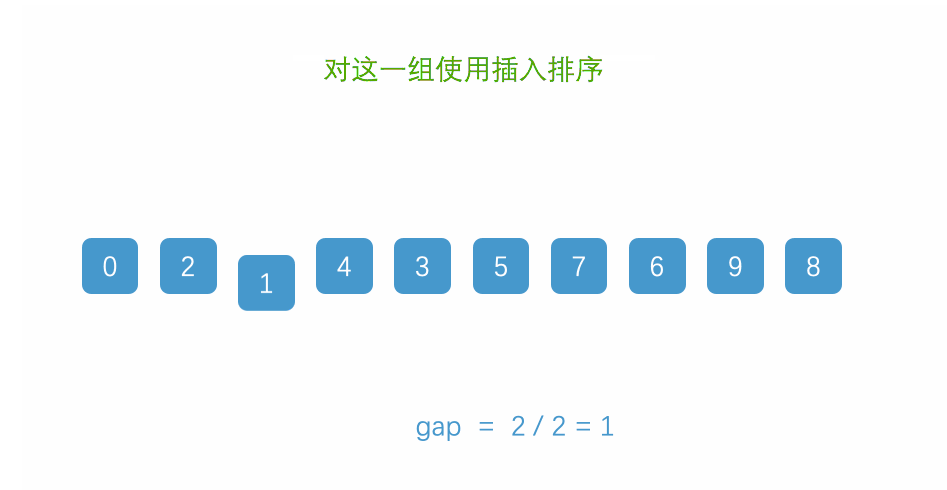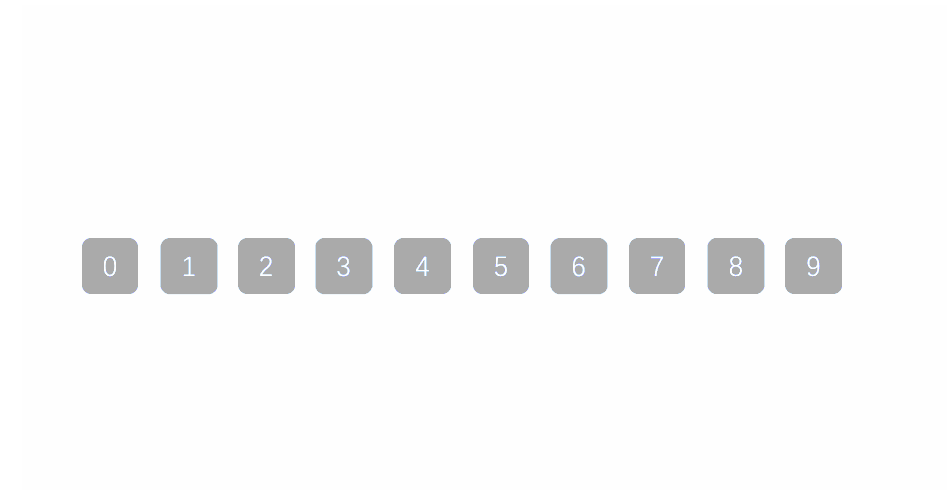
gap越大,跳的就越快,但是接近有序的速度会很慢。
gap越小,跳的就越慢,但是接近有序的速度就会快很多。
那gap到底如何进行取值呢?其实,gap不应该是具体的某个值,gap应该是发生变化的
请看代码:
void ShellSort(int* a, int n)
{
int gap = n;
while (gap > 1)
{
gap /= 2;
//多组并排
for (int i = 0; i < n - gap; i++)
{
int end = i;
int tmp = a[i + gap];
while (end >= 0)
{
if (tmp < a[end])
{
a[end + gap] = a[end];
end -= gap;
}
else
{
break;
}
}
a[end + gap] = tmp;
}
PrintArray(a, n);
printf("\n");
}
}
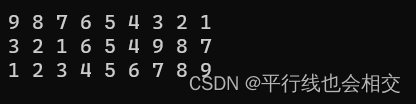
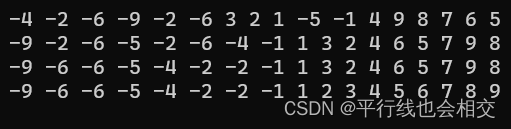
比如,我对下面这个数组进行排序:

下面是运行结果:

所以,我们通过对gap进行动态调整可以一次性把这个数组排序完,就没有所谓的第一步第二步了,因为gap/=2,所以最后gap会变成1,就相当于插入排序了。
总结一下:
当
gap>1的时候是对数组进行预排序;当gap==1的时候才是对数组进行直接插入排序。
希尔排序的时间复杂度
关于希尔排序时间复杂度的分析,这里就简单提一嘴,就不细说了。因为希尔排序时间复杂度的分析是很难进行分析的,所以感兴趣的直接去看。这里直接给出希尔排序的结论了:希尔排序的时间复杂度可以按照n1.25~n*n1.25之间来进行计算。
希尔排序总代码
#include<stdio.h>
void PrintArray(int* a, int n)
{
for (int i = 0; i < n; i++)
{
printf("%d ", a[i]);
}
}
void TestShellSort()
{
int a[] = { 9,8,7,6,5,4,3,2,1,-5,-2,-6,-4,-2,-6,-9,-1 };
//PrintArray(a, sizeof(a) / sizeof(a[0]));
//printf("\n");
ShellSort(a, sizeof(a) / sizeof(a[0]));
//PrintArray(a, sizeof(a) / sizeof(a[0]));
//printf("\n");
}
void ShellSort(int* a, int n)
{
//int gap = 3;
一组排完再排另一组
//for (int j = 0; j < gap; j++)
//{
// for (int i = gap + j; i < n; i += gap)
// {
// int end = i - gap;;
// int tmp = a[i];
// while (end >= 0)
// {
// if (tmp < a[end])
// {
// a[end + gap] = a[end];
// end -= gap;
// }
// else
// {
// break;
// }
// }
// a[end + gap] = tmp;
// }
for (int i = 0 + j; i < n - gap; i += gap)
{
int end = i;;
int tmp = a[i + gap];
while (end >= 0)
{
if (tmp < a[end])
{
a[end + gap] = a[end];
end -= gap;
}
else
{
break;
}
}
a[end + gap] = tmp;
}
}
//}
int gap = n;
while (gap > 1)
{
gap = gap / 3 + 1;
//gap /= 2;
//多组并排
for (int i = 0; i < n - gap; i++)
{
int end = i;
int tmp = a[i + gap];
while (end >= 0)
{
if (tmp < a[end])
{
a[end + gap] = a[end];
end -= gap;
}
else
{
break;
}
}
a[end + gap] = tmp;
}
PrintArray(a, n);
printf("\n");
}
}
int main()
{
TestShellSort();
return 0;
}
选择排序
插入排序其实就好比我们玩斗地主,在摸牌的时候我们先不对牌进行排序,等到摸完牌之后我们再对手里的这些乱序的牌进行排序,即从大到小或者从小到大进行排序。直接选择排序的过程就是与此相类似。
学习直接选择排序之前我们先来看一看直接选择排序的动态图:
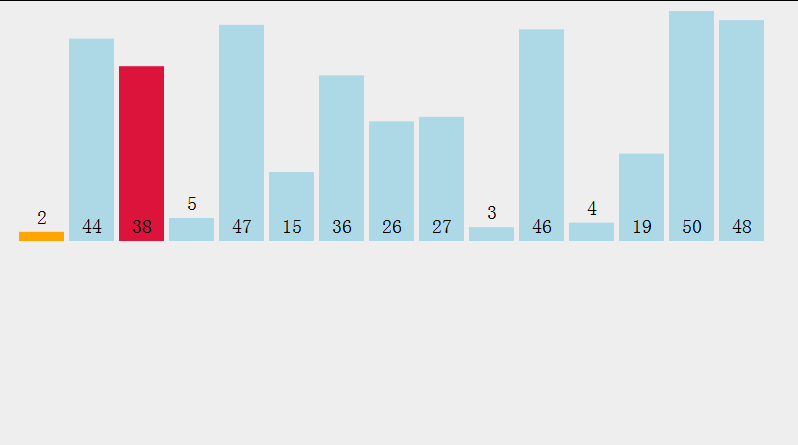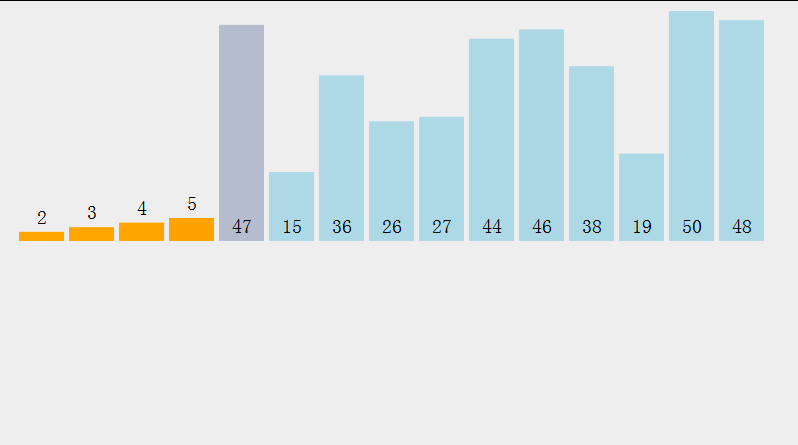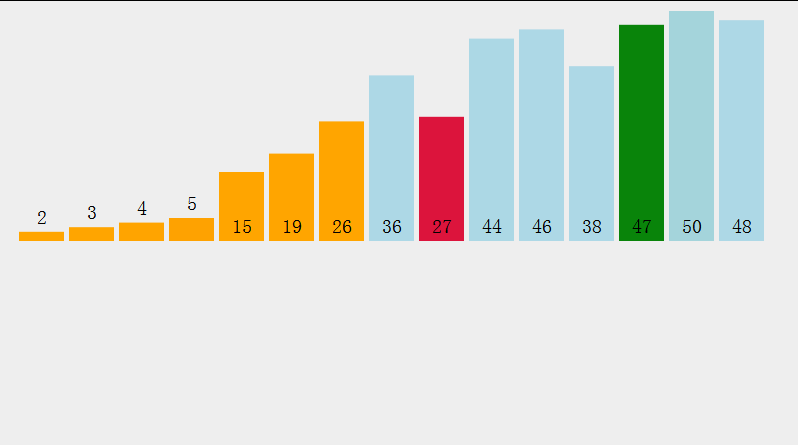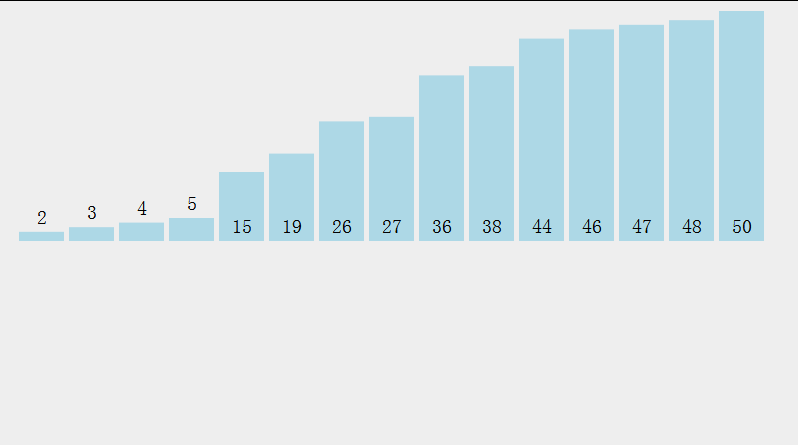
上图是按照升序进行排序的,即每一轮的比较我们可以把最小的一个数筛选出来放到最左边,但是我们可以对其进行优化,我们筛选最小的数的同时还可以把最大的数筛选出来放到最右边。所以每一轮比较我们可以把最小的和最大的数同时筛选出来分别放到最左边和最右边。
这个排序虽然简单,但是这个排序非常不稳定,实际上也很少用这个排序。
直接选择排序代码
void SelectSort(int* a, int n)
{
int left = 0;
int right = n - 1;
while (left < right)
{
int mini = left;
int maxi = left;
for (int i = left + 1; i <= right; i++)
{
if (a[i] < a[mini])
{
mini = i;
}
if (a[i] > a[maxi])
{
maxi = i;
}
}
Swap(&a[left], &a[mini]);
if (left == maxi)
{
maxi = mini;
}
Swap(&a[right], &a[maxi]);
left++;
right--;
}
}
关于这个直接选择排序的话,有一点需要我们特别注意。就是当我们的left与maxi重叠的时候,请看举例:
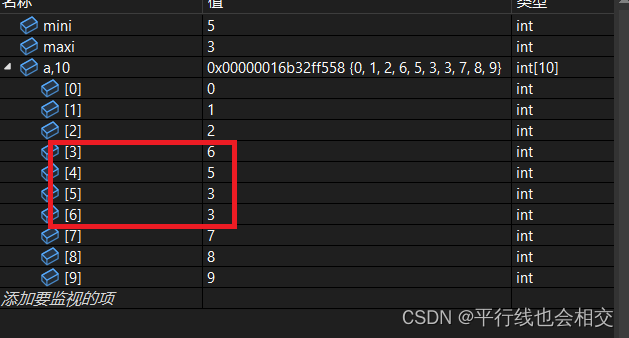
上面举例中,mini是5;maxi是3没有错,这里特殊就特殊在这里的maxi与left重叠了,所以当我们的left和mini交换完之后,即:
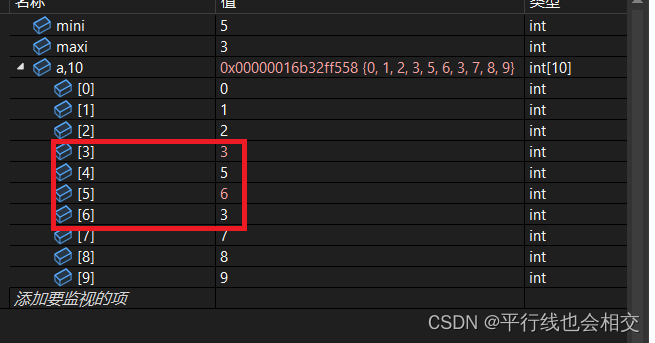
此时交换前的mini正好把处于left位置的maxi进行覆盖了,所以下次交换就会导致出现错误。
请看:
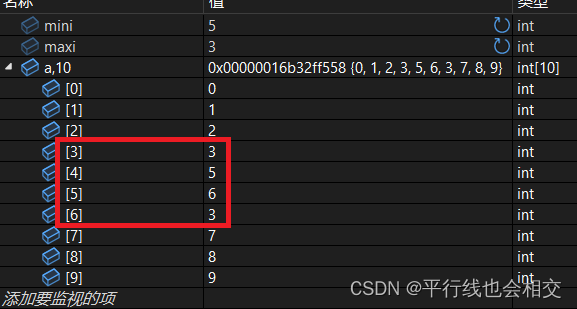
上图中的a[6]的位置本应该是6,但是就是因为maxi与left重叠了,所以就会出错,所以我们在进行第二次交换之前需要判断是否maxi与left会重叠,即:
if (left == maxi)
{
maxi = mini;
}
这就是直接交换排序比较容易忽略的一个点,需要我们特别注意。
最终运行结果如下:

直接选择排序时间复杂度及总结
选择排序时间复杂度的话,无论最好情况还是最坏情况时间复杂度都是O(N^2)。
总结一下直接选择排序的特点:
1.我们单单从时间复杂度的角度来看就可以知道直接选择排序的效率并不高。因为无论数据有序还是比较有序又或者是乱序对于直接选择排序而言都没有太大的区别。所以直接选择排序真的是毫无技巧可言,直接硬生生地遍历一遍数据,给我一种软硬不吃的感觉😄。
2.时间复杂度:O(N^2)。
3.空间复杂度:O(1)。
以上就是八大排序算法的一部分,主要讲解的是插入排序、希尔排序、选择排序。
好了,就到这里吧,一起加油,再见啦各位!!!