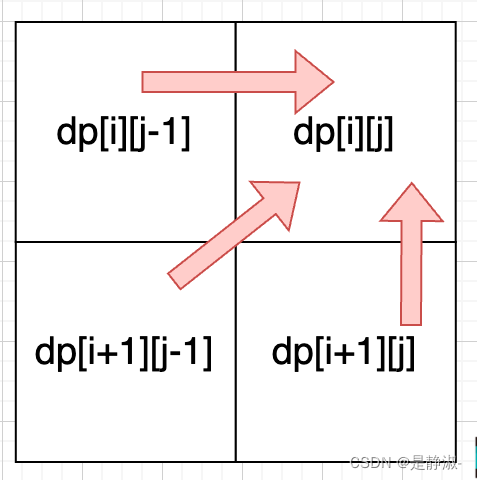
今天是周末,也就不为难自己了,学习了一下floyed算法(确实简单哈哈),这个算法也是最短路的一种
在一副图中,a到b的距离可能不是直接的ab边最短,这时候就要用到floyed的思想了,可能是a到c到b比直接a到b最短.所以我们要枚举一边才可以知道a到b的最短的路线
这就是floyed的大概
核心的代码也很简单
for(int h=1;h<=n;h++){//floyed
for(int g=1;g<=n;g++){
for(int b=1;b<=n;b++){
if(h!=g&&g!=b&&b!=h&&a[g][b]>a[g][h]+a[h][b])
a[g][b]=a[g][h]+a[h][b];
}
}
}
就这末一点点 (很暴力,我一点也不喜欢)
但对于数据不大的题目还是非常的友好的(因为好写)
这是有边权的,要是没有边权,那么就只要判断0或者1就好了
学了就要训练一下
# 医院设置
## 题目描述
设有一棵二叉树,如图:
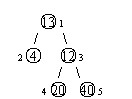
其中,圈中的数字表示结点中居民的人口。圈边上数字表示结点编号,现在要求在某个结点上建立一个医院,使所有居民所走的路程之和为最小,同时约定,相邻接点之间的距离为 $1$。如上图中,若医院建在1 处,则距离和 $=4+12+2\times20+2\times40=136$;若医院建在 $3$ 处,则距离和 $=4\times2+13+20+40=81$。
## 输入格式
第一行一个整数 $n$,表示树的结点数。
接下来的 $n$ 行每行描述了一个结点的状况,包含三个整数 $w, u, v$,其中 $w$ 为居民人口数,$u$ 为左链接(为 $0$ 表示无链接),$v$ 为右链接(为 $0$ 表示无链接)。
## 输出格式
一个整数,表示最小距离和。
## 样例 #1
### 样例输入 #1
```
5
13 2 3
4 0 0
12 4 5
20 0 0
40 0 0
```
### 样例输出 #1
```
81
```
## 提示
#### 数据规模与约定
对于 $100\%$ 的数据,保证 $1 \leq n \leq 100$,$0 \leq u, v \leq n$,$1 \leq w \leq 10^5$。
出自洛谷:P1364 医院设置 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
格式有问题,看不懂就点链接.
用floyed我们很简单的就可以得出,各个点到其他所有的点的距离,再乘上其他点的人口,就可以得到,建立此点位置距离和,求出每个位置的距离和取最小的就是答案
ok上代码看看
#include<stdio.h>
int map[101][101];
int h[101];
int n;
void newr(){
for(int h=1;h<=n;h++){
for(int g=1;g<=n;g++)
map[h][g]=1000000;
}
}
void floyed(){
for(int j=1;j<=n;j++)
for(int h=1;h<=n;h++)
for(int gh=1;gh<=n;gh++){
if(j!=gh&&j!=h&&h!=gh&&map[h][gh]>map[h][j]+map[j][gh]){
map[h][gh]=map[h][j]+map[j][gh];
}
}
}
int main(){
scanf("%d",&n);
int jj,kk;
newr();
for(int j=1;j<=n;j++){
map[j][j]=0;
scanf("%d%d%d",&h[j],&jj,&kk);
if(jj!=0)
map[jj][j]=map[j][jj]=1;
if(kk!=0)
map[kk][j]=map[j][kk]=1;
}
floyed();
int min=999999999;
for(int kl=1;kl<=n;kl++){
int sum=0;
for(int y=1;y<=n;y++){
sum+=map[kl][y]*h[y];
}
if(sum<min)
min=sum;
}
printf("%d\n",min);
return 0;
}简单的鸭皮,练习刚刚好的呀
再来
题目描述
如下图所示的一棵二叉树的深度、宽度及结点间距离分别为:
- 深度:44
- 宽度:44
- 结点 8 和 6 之间的距离:88
- 结点 7 和 6 之间的距离:33
其中宽度表示二叉树上同一层最多的结点个数,节点 �,�u,v 之间的距离表示从 �u 到 �v 的最短有向路径上向根节点的边数的两倍加上向叶节点的边数。
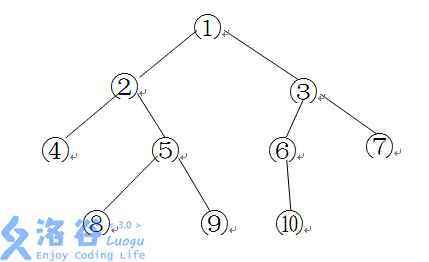
给定一颗以 1 号结点为根的二叉树,请求出其深度、宽度和两个指定节点 �,�x,y 之间的距离。
输入格式
第一行是一个整数,表示树的结点个数 �n。
接下来 �−1n−1 行,每行两个整数 �,�u,v,表示树上存在一条连接 �,�u,v 的边。
最后一行有两个整数 �,�x,y,表示求 �,�x,y 之间的距离。
输出格式
输入三行,每行一个整数,依次表示二叉树的深度、宽度和 �,�x,y 之间的距离。
输入输出样例
输入 #1复制
10 1 2 1 3 2 4 2 5 3 6 3 7 5 8 5 9 6 10 8 6
输出 #1复制
4 4 8
说明/提示
对于全部的测试点,保证 1≤�,�,�,�≤�≤1001≤u,v,x,y≤n≤100,且给出的是一棵树。
直接复制还可以看见图,还是直接复制吧
好家伙数据量不大才100而已,我觉得floyed完全可以的
1深度 就是点1到其他的点距离的最大值
2宽度,每次遍历点1到其他点的时候距离就代表点的参数记录下来取点最多的层数就可以了
3x到y的距离,向根结点的边数乘以2,就是向根节点找的边就得乘以2,那我们就把子节点向上的边权变成2就好拉,用了floyed得到的就是答案了
ok上代码
#include<stdio.h>
int a[101][101];
int b[101]={0};
int n,x,y;
void newr(){
for(int f=1;f<=n;f++){
for(int g=1;g<=n;g++){
a[f][g]=100000;
}
}
}
int main(){
int jj,kk;
scanf("%d",&n);
newr();
for(int h=1;h<n;h++){
scanf("%d%d",&jj,&kk);
a[jj][kk]=1;
a[kk][jj]=2;
}
for(int h=1;h<=n;h++){//floyed
for(int g=1;g<=n;g++){
for(int b=1;b<=n;b++){
if(h!=g&&g!=b&&b!=h&&a[g][b]>a[g][h]+a[h][b])
a[g][b]=a[g][h]+a[h][b];
}
}
}
scanf("%d%d",&x,&y);
int maxr=1,maxd=1;
for(int h=2;h<=n;h++){
maxr=maxr>a[1][h]?maxr:a[1][h];
b[a[1][h]]++;//记录第几层有几个节点
}
for(int h=1;h<=maxr;h++){//有多深就有几层
maxd=maxd>b[h]?maxd:b[h];
}
printf("%d\n",maxr+1);
printf("%d\n",maxd);
printf("%d\n",a[x][y]);
return 0;
}理解了,几个要求的值咋来的题目就很简单了,还是因为数据小了,可以偷偷的溜
不然不会折磨简单的呀
ok ok
到这就算了
撒花谢幕!!!!