一、本周周赛总结

• 这周都还挺难的。
• T1 判断质数。
• T2 预处理+前缀和+二分。
• T3 二分答案。
• T4 并查集优化剪枝转移状态的BFS（和上周一样）。

二、 6361. 对角线上的质数

链接: 6361. 对角线上的质数

1. 题目描述

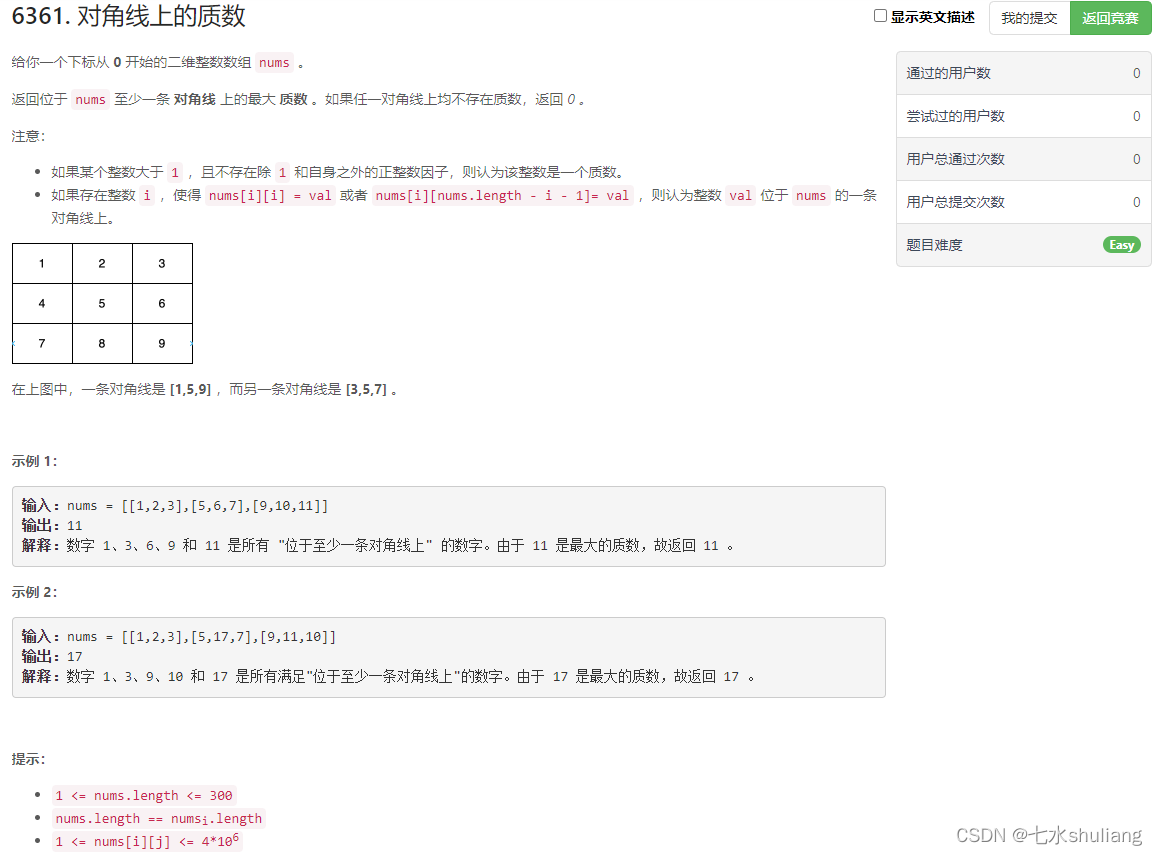
2. 思路分析

按题意模拟即可。

• 由于数据范围4e6，没敢上筛；但是n小，所以暴力了（其实可以上筛）；结果没判断1是合数，结果wa了。。

---

• 这题证明了py的埃氏筛就是比欧拉筛快。
• 
  
• 

3. 代码实现

class Solution:
    def diagonalPrime(self, nums: List[List[int]]) -> int:
        p = set()
        m,n = len(nums),len(nums[0])
        for i in range(n):
            p.add(nums[i][i])
            p.add(nums[i][n-i-1])
            
        def is_prime(x):            
            if x <=1:
                return False
            if x == 2 or x == 3:
                return True 
            for i in range(2,int(x**0.5)+1):
                if x % i ==0:
                    return False 
            return True
           
            
        ans = 0
        for x in p:
            if is_prime(x):
                ans = max(ans,x)
        return ans

三、6360. 等值距离和

链接: 6360. 等值距离和

1. 题目描述

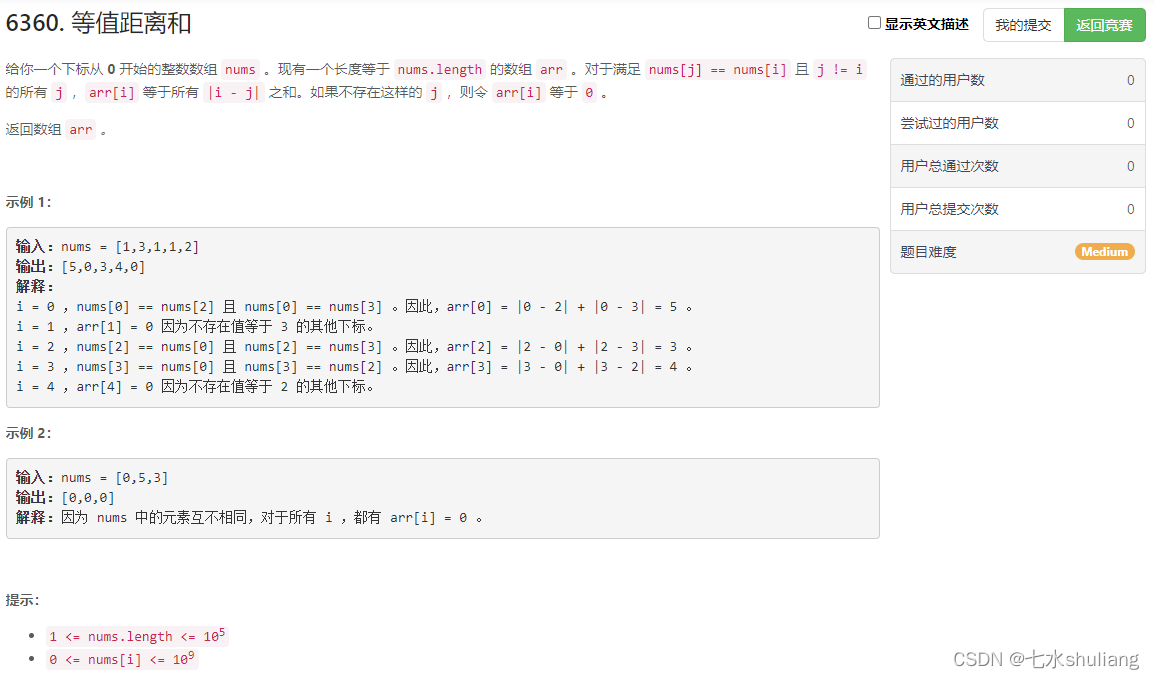
2. 思路分析

• 一看考过差不多的，但是要分组。
• 忘记预处理Tle。。
• 按值分组，记录下标列表。
• 对每个位置i，二分对应的列表找到i的位置。
• 那么ans[i]可以用前缀和/后缀和计算了。

3. 代码实现

class Solution:
    def distance(self, nums: List[int]) -> List[int]:
        n = len(nums)
        d = defaultdict(list)
        for i,v in enumerate(nums):
            d[v].append(i)
        pres = defaultdict(list)
        for k,v in d.items():
            pres[k] =  [0] + list(accumulate(v))
        ans = [0] * n
        for i,v in enumerate(nums):
            p = d[v]
            n = len(p)
            if len(p)<=1:
                continue 
            pre = pres[v]
            pos = bisect_left(p,i)
            # print(p,pre,pos)
            ans[i] = i*(pos+1) - pre[pos+1] + pre[-1] - pre[pos+1] - i*(n-pos-1)
        return ans

四、6359. 最小化数对的最大差值

链接: 6359. 最小化数对的最大差值

1. 题目描述

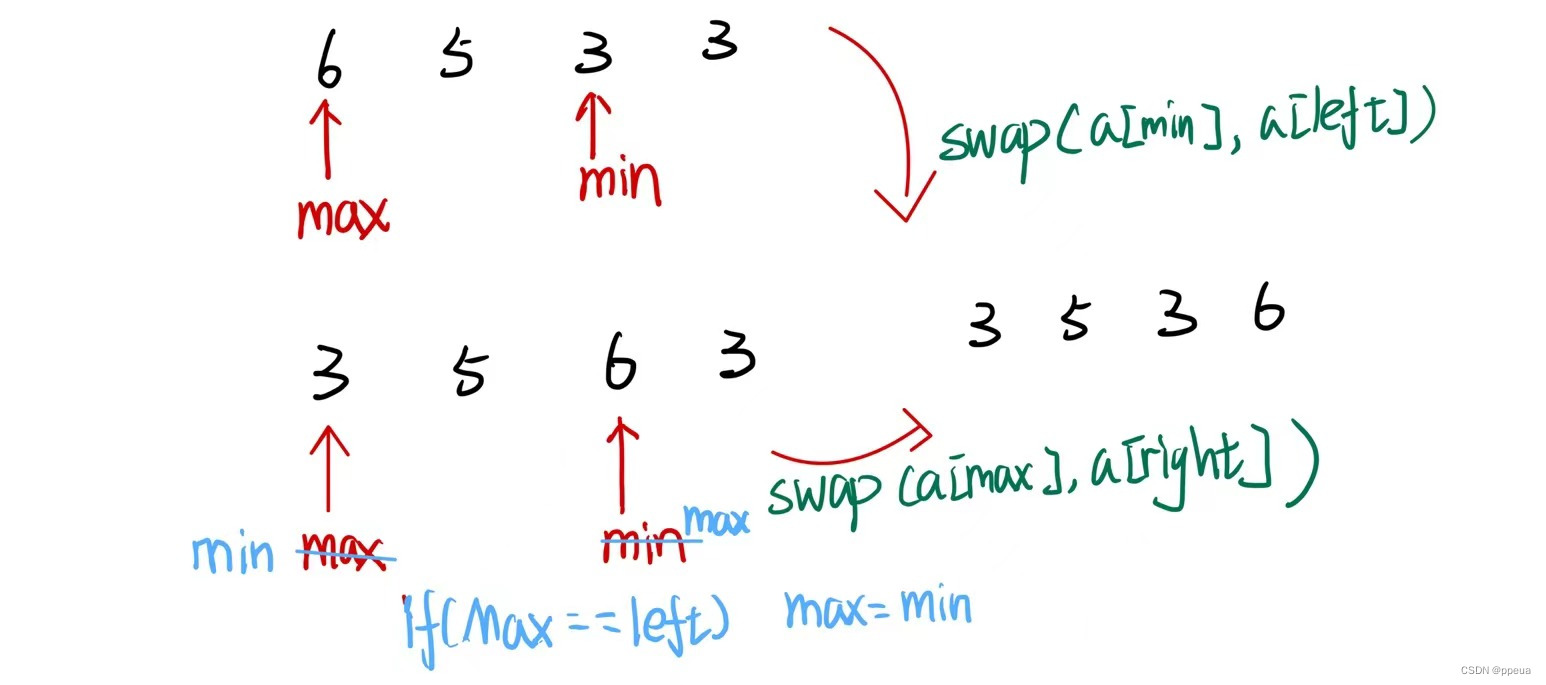
2. 思路分析

最大值最小化，警觉。

• 最大值最小化等价于二分答案。
• 设f(x)为选出的序列中最大差值不超过x时，能否找到s对序列。
• 显然，若f(x)==True,则f(x+1)一定是True，f(x-1)不一定，因此有二段性。找到最小的x即可。
• f(x)怎么写呢，要让差值尽可能小，考虑每个数，排序后和相邻的数据组合就是最小值。
• 贪心的试图组合每个数即可。你可能会质疑贪心的正确性:考虑(a,b,c,d)，若ab能组合，那会使选出的对+1；如果不组合，b也只可能跟后边的c组合，而且占用了c，不会使答案更优。

3. 代码实现

class Solution:
    def minimizeMax(self, nums: List[int], p: int) -> int:
        n = len(nums)
        nums.sort()
        
        def ok(x):
            s = 0
            i  = 0
            while i < n-1:
                if nums[i+1] - nums[i] <= x:
                    s += 1
                    i += 1
                i += 1
            return s >= p 
        
        return bisect_left(range(10**9+1),True,key=ok)    

五、 6353. 网格图中最少访问的格子数

链接: 6353. 网格图中最少访问的格子数

1. 题目描述

2. 思路分析

没想到出了上周T4的加强版。

• 乍一看是普通BFS最短路，但是由于转移目标是一个range(注意是连续的范围)，暴力转移可能会TLE。
• 因此可以用有序集合或者并查集删除，转移时直接通过数据结构找下一个转移目标，这样每个目标只会被访问一次，就可以AC啦！
• 时间复杂度O(nm),这里认为并查集的均摊复杂度是O(1)。

---

• 对每行每列都建立独立的并查集，一共m+n个。
• 当访问(x,y)后，把它和右边/下边的坐标连接，union对应的(x,y+1)和(x+1,y+1)，这样就等于删除(x,y)。
• 我提交的版本没有连接另一个方向的坐标，也过了，但是跑得慢一点。应该是不影响正确性的，但每个坐标要访问两次了。

3. 代码实现。

class DSU:
    def __init__(self, n):
        self.fathers = list(range(n))

    def find_fa(self, x):
        fs = self.fathers
        t = x
        while fs[x] != x:
            x = fs[x]
        while t != x:
            fs[t], t = x, fs[t]
        return x

    def union(self, x: int, y: int) -> bool:
        x = self.find_fa(x)
        y = self.find_fa(y)

        if x == y:
            return False
        # if self.size[x] > self.size[y]:  # 注意如果要定向合并x->y，需要干掉这个；实际上上边改成find_fa后，按轶合并没必要了，所以可以常关
        #     x, y = y, x
        self.fathers[x] = y
        return True

class Solution:
    def minimumVisitedCells(self, grid: List[List[int]]) -> int:
        m,n = len(grid),len(grid[0])
        if m==n==1:
            return 1
        def inside(x,y):
            return 0<=x<m and 0<=y<n
        rows = [DSU(n+1) for _ in range(m)]
        cols = [DSU(m+1) for _ in range(n)]
        ans = 1
        q = deque([(0,0)])
        rows[0].union(0,1)
        cols[0].union(0,1)
        while q:
            ans += 1
            for _ in range(len(q)):
                x,y = q.popleft()
                if x == m-1 and y == n-1:
                    return ans - 1
                mn,mx = min(y+1,n-1),min(grid[x][y]+y,n-1)
                dsu1,dsu2 = rows[x],cols[y]
                while mn <= mx:
                    mn = dsu1.find_fa(mn)
                    if mn <= mx:
                        if x == m-1 and mn == n-1:
                            return ans
                        q.append((x,mn))
                        dsu1.union(mn,mn+1)
                        cols[mn].union(x,x+1)
                        mn += 1
                        
                mn,mx = min(x+1,m-1),min(grid[x][y]+x,m-1)
                
                while mn <= mx:
                    mn = dsu2.find_fa(mn)
                    if mn <= mx:
                        if mn == m-1 and y == n-1:
                            return ans
                        q.append((mn,y))
                        dsu2.union(mn,mn+1)
                        rows[mn].union(y,y+1)
                        mn += 1                                
                
        return -1       

六、参考链接