打卡24天，今天学第七章回溯算法，之前已经学过一遍，现在学第二遍，加油。

今日任务

• 理论基础
• 77.组合

理论基础

什么是回溯

递归的副产物，有递归就会有回溯

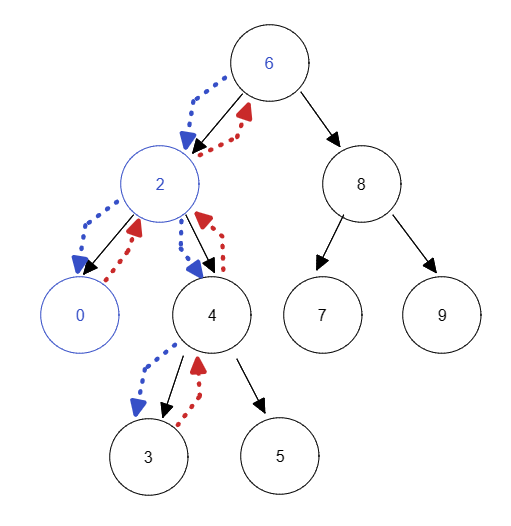
红色的箭头就是回溯

回溯的效率

回溯的本质是穷举，穷举所有可能，然后选出我们想要的答案，如果想让回溯法高效一些，可以加一些剪枝的操作，但也改不了回溯法就是穷举的本质，所以回溯法的效率不高。

回溯解决的问题

• 组合问题
• 排列问题
• 子集问题：一个N个数的集合里有多少符合条件的子集
• 切割问题
• 棋盘问题：n皇后问题、解数独

如何用回溯法

所有回溯法解决的问题都可以抽象为树形结构。

因为回溯法解决的都是在集合中递归查找子集，集合的大小就构成了树的宽度，递归的深度，都构成的树的深度。

递归就要有终止条件，所以必然是一棵高度有限的树（N叉树）。

回溯法模板

回溯函数模板返回值以及参数

• 回溯算法中函数返回值一般为void。

• 回溯算法需要的参数可不像二叉树递归的时候那么容易一次性确定下来，所以一般是先写逻辑，然后需要什么参数，就填什么参数。

void backtracking(参数)

回溯法的终止条件

什么时候达到了终止条件，树中就可以看出，一般来说搜到叶子节点了，也就找到了满足条件的一条答案，把这个答案存放起来，并结束本层递归。

if (终止条件) {
    存放结果;
    return;
}

回溯搜索的遍历过程

for (选择：本层集合中元素（树中节点孩子的数量就是集合的大小）) {
    处理节点;
    backtracking(路径，选择列表); // 递归
    回溯，撤销处理结果
}

for循环就是遍历集合区间，可以理解一个节点有多少个孩子，这个for循环就执行多少次。

backtracking这里自己调用自己，实现递归。

大家可以从图中看出for循环可以理解是横向遍历，backtracking（递归）就是纵向遍历，这样就把这棵树全遍历完了，一般来说，搜索叶子节点就是找的其中一个结果了。

77.组合

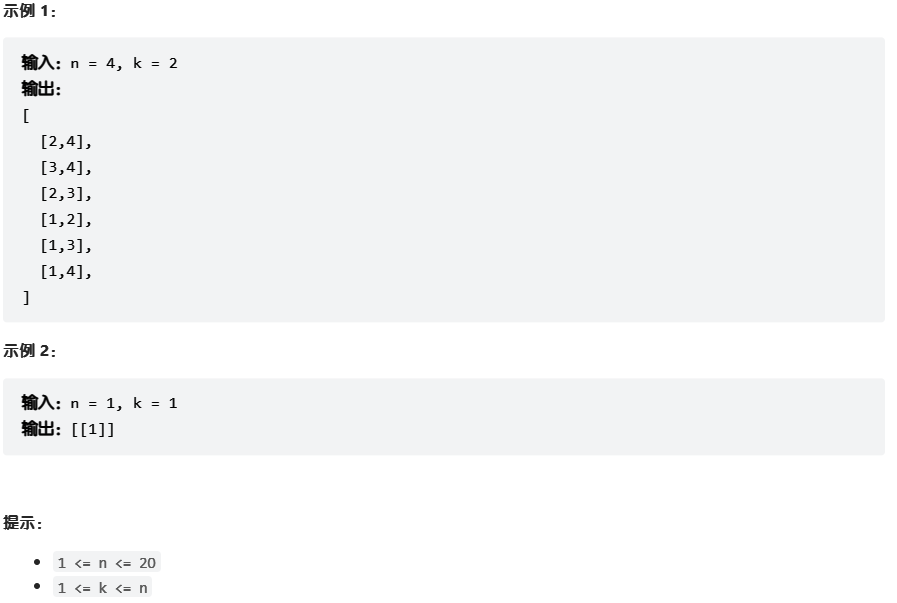
给定两个整数 n 和 k，返回范围 [1, n] 中所有可能的 k 个数的组合。
你可以按 任何顺序 返回答案。

代码随想录

• 抽象成树形结构
  
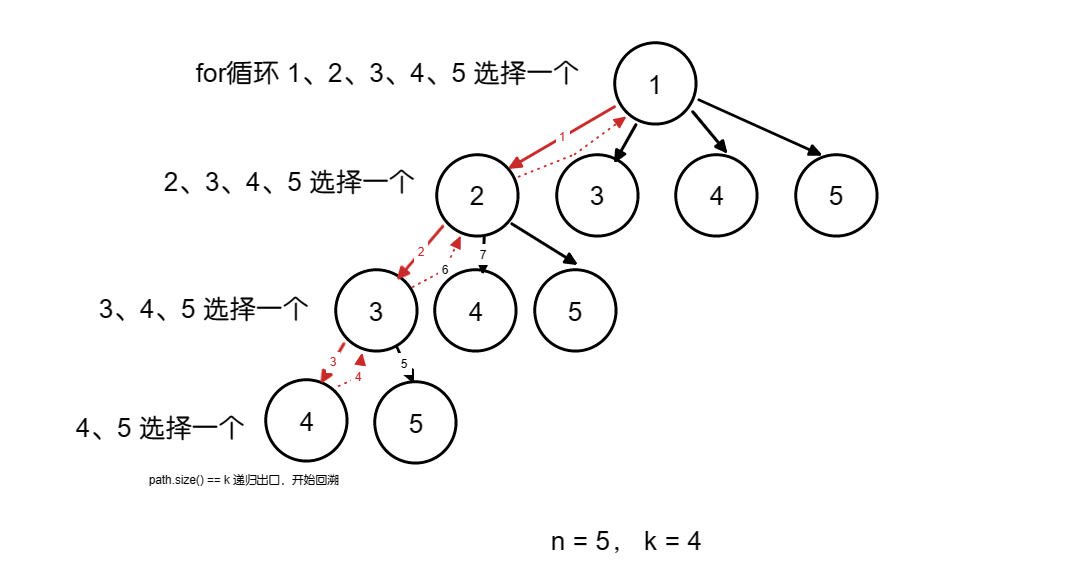
  结点只是画出一部分，右边空白区还有结点的

• 定义一个二维数组res，存放结果集，定义一个以为数组path，用来存放符合条件的结点

• 确定递归出口：当 path 的长度等于 k ，说明已经收集到另一个结果，存入结果集

• 单层逻辑

  for (int i = startIndex; i <= n; i++) { // 控制树的横向遍历
  	path.push_back(i); // 处理节点 
  	backtracking(n, k, i + 1); // 递归：控制树的纵向遍历，注意下一层搜索要从i+1开始
  	path.pop_back(); // 回溯，撤销处理的节点
  }
  

• 发现需要参数 n ，k， 还需要每次从startIndex开始遍历。

class Solution {
public:
    vector<vector<int> > res;
    vector<int> path;
    void backtracking(int n, int startIndex, int k) {
        if(path.size() == k) {
            res.push_back(path);
            return ;
        }
        for(int i = startIndex; i <= n; i++) {
            path.push_back(i);
            backtracking(n, i + 1, k);
            path.pop_back();
        }

    }
    vector<vector<int>> combine(int n, int k) {
        res.clear();
        path.clear();
        backtracking(n, 1, k);
        return res;
    }
};

优化剪枝
当 n = 4， k = 4，那么第一层for循环的时候，从元素2开始的遍历都没有意义了。 在第二层for循环，从元素3开始的遍历都没有意义了。

所以优化之后的for循环是：

for (int i = startIndex; i <= n - (k - path.size()) + 1; i++) // i为本次搜索的起始位置