一、并查集
1)有若干个样本a、b、c、d…类型假设是V
2)在并查集中一开始认为每个样本都在单独的集合里
3)用户可以在任何时候调用如下两个方法:
boolean isSameSet(V x, V y) : 查询样本x和样本y是否属于一个集合
void union(Vx, V y) : 把x和y各自所在集合的所有样本合并成一个集合
4) isSameSet和union方法的代价越低越好
1)每个节点都有一条往上指的指针
2)节点a往上找到的头节点,叫做a所在集合的代表节点
3)查询x和y是否属于同一个集合,就是看看找到的代表节点是不是一个
4)把x和y各自所在集合的所有点合并成一个集合,只需要小集合的代表点挂在大集合的代表点的下方即可
二、并查集的优化
1)节点往上找代表点的过程,把沿途的链变成扁平的
2)小集合挂在大集合的下面
3)如果方法调用很频繁,那么单次调用的代价为O(1),两个方法都如此
三、并查集的应用
解决两大块区域的合并问题
常用在图等领域中
四、代码演示:
package class14;
import java.util.HashMap;
import java.util.List;
import java.util.Stack;
/** 并查集
* 有若干个样本a、b、c、d…类型假设是V
* 在并查集中一开始认为每个样本都在单独的集合里
* 用户可以在任何时候调用如下两个方法:
* boolean isSameSet(V x, V y) : 查询样本x和样本y是否属于一个集合
* void union(V x, V y) : 把x和y各自所在集合的所有样本合并成一个集合
* isSameSet和union方法的代价越低越好
*
* 1)每个节点都有一条往上指的指针
* 2)节点a往上找到的头节点,叫做a所在集合的代表节点
* 3)查询x和y是否属于同一个集合,就是看看找到的代表节点是不是一个
* 4)把x和y各自所在集合的所有点合并成一个集合,只需要小集合的代表点挂在大集合的代表点的下方即可
*
* 重点优化:
* 1)节点往上找代表点的过程,把沿途的链变成扁平的
* 2)小集合挂在大集合的下面
* 3)如果方法调用很频繁,那么单次调用的代价为O(1),两个方法都如此
*
* 并查集的应用
* 解决两大块区域的合并问题
* 常用在图等领域中
*
*/
public class UnionFind {
//自定义泛型节点类,用来将V类型的样本数据封装到类进行处理
public static class Node<V>{
public V value;
public Node(V v){
value = v;
}
}
//并查集类
public static class Union_Find<V>{
//nodes是存放的样本数据对应的样本封装类的一个哈希表。 比如节点 V 是int类型 1, 那么我们处理的时候,就通过map.get(1)来转换node类型处理
public HashMap<V,Node<V>> nodes;
//heads是存放每个节点所在集合的头节点,key的头节点是value 比如a->b->c a的头节点就是c b的头节点就是c c的头节点就是c
public HashMap<Node<V>,Node<V>> heads;
//sizeMap是表示每个集合的头节点,这个集合有多少个节点 包含自己 比如a->b->c 这个集合c是头节点 那么对应的有3个节点大小
public HashMap<Node<V>,Integer> sizeMap;
//初始化构造函数 我们假设传入的是list<V>泛型集合
public Union_Find(List<V> values){
//先给三个属性new个哈希表 再将节点集合添加到哈希表
nodes = new HashMap<>();
heads = new HashMap<>();
sizeMap = new HashMap<>();
for(V v:values){
Node<V> node = new Node<>(v);
//封装节点类对应的键值对、 节点的头节点初始是自身 、 集合头节点当前为1
nodes.put(v,node);
heads.put(node,node);
sizeMap.put(node,1);
}
}
//找到给节点所在集合的头节点。 比如 a->b->c cur为a节点 那么返回的头节点是c
public Node<V> findFather(Node<V> cur){
//定义一个栈,把节点往上的父节点都依次入栈
Stack<Node<V>> stack = new Stack<>();
//退出的条件就是当节点来到该节点所在集合的头节点 那么就退出,cur就会来到头节点
while(cur != heads.get(cur)){
stack.push(cur);
cur = heads.get(cur);
}
//此时cur退出循环时,就会来到头节点
//接着关键优化:把这个链条上的全部节点 都扁平化,每个节点都直接指向头节点cur 比如 a->b->c 优化成a->c b-c c->c 减少中间需要遍历的节点
while(!stack.isEmpty()){
heads.put(stack.pop(),cur);
}
return cur;
}
//判断两节点是否在一个集合
public boolean isSameSet(V a,V b){
//比较两者的所在的集合的头节点是否相等
return findFather(nodes.get(a)) == findFather(nodes.get(b));
}
//合并两个节点所在的集合 小集合头节点指向大集合头节点 然后删除小集合的头节点记录
public void union(V a, V b){
//先取出两节点所在集合的头节点
Node<V> aHead = findFather(nodes.get(a));
Node<V> bHead = findFather(nodes.get(b));
if(aHead != bHead){
//不相等 表示不同集合 需要合并 相等就是同集合不用合并了
//先判断两节点的头节点入参取集合大小
int aSetSize = sizeMap.get(aHead);
int bSetSize = sizeMap.get(bHead);
//分好大小
Node<V> big = aSetSize >= bSetSize ? aHead : bHead;
Node<V> small = big == aHead ? bHead : aHead;
//就将小头节点 指向大头节点 添加到头节点表
heads.put(small,big);
//刷新大头节点集合大小
sizeMap.put(big,aSetSize+bSetSize);
//合并完 需要把小头节点从集合大小移除,因为小头节点合并到大头节点了
sizeMap.remove(small);
}
}
//返回集合个数
public int sets(){
return sizeMap.size();
}
}
}
五、Leetcode 547. Friend Circles
package class15;
// 本题为leetcode原题 547. 省份数量
// 测试链接:https://leetcode.com/problems/friend-circles/
// 可以直接通过
/**
* 有 n 个城市,其中一些彼此相连,另一些没有相连。如果城市 a 与城市 b 直接相连,且城市 b 与城市 c 直接相连,那么城市 a 与城市 c 间接相连。
* 省份 是一组直接或间接相连的城市,组内不含其他没有相连的城市。
* 给你一个 n x n 的矩阵 isConnected ,其中 isConnected[i][j] = 1 表示第 i 个城市和第 j 个城市直接相连,而 isConnected[i][j] = 0 表示二者不直接相连。
* 返回矩阵中 省份 的数量。
*
* 思路:
* 通过并查集方式解决。 正方形矩阵,根据题意提示 [i][j]=1 那么[j][i]也是=1 两个横纵坐标在矩阵中是对称的
* 所以遍历右上角元素即可,对角线以下都是对称的 而对称点都是自身[0][0] [1][1] .. 默认值肯定都是1 跳过不需判断
* 看上半部分 元素值为1 那么我们就调用union合并两个i,j 如果已经是一个区域那么就不走逻辑,不在一个区域合并,并且集合-1
* 最后返回 set集合个数 就是表示相连的省份
*
*/
public class FriendCircles {
public static int findCircleNum(int[][] M) {
//矩阵是正方形,取出长度N
int N = M.length;
//定义并查集,我们判断的是两个横纵坐标是否在一个区域,M[N][N]最大边界索引是N 所以初始化大小N
UnionFind unionFind = new UnionFind(N);
for(int i = 0;i<N;i++){
for(int j = i + 1; j < N;j++){
//遍历的矩阵上半部分即可,对角线是自身不需判断,下半部分是跟上半部分对称的 也省去遍历
if(M[i][j] == 1){
//只有i j 两个城市这个关系是1 有相连,我们再进行并查集合并操作
unionFind.union(i,j);
}
}
}
//最后返回并查集的集合个数 就表示城市相连的个数
return unionFind.set;
}
//定义并查集类,源数据是数组,之前我们采用的哈希表,更多时候采用数组性能更优
public static class UnionFind{
public int[] parent; //存放每个节点所在区域的头节点,初始化是自身 parent[i]=i
public int[] size; //头节点i 的所在区域的大小 初始化 size[i] = 1 自己就一个
public int set; //判断集合个数 初始化,每个节点就是一个set
public int[] help; //辅助数组,用来做优化,在findparent时,就扁平化 该同区域的数组,直接指向头节点
public UnionFind(int N){
parent = new int[N];
size = new int[N];
set = N;
help = new int[N];
for(int i = 0;i<N;i++){
parent[i] = i; //初始化i节点所在区域就只有自己 头节点也就是自己
size[i] = 1; //大小就是自身一个
}
}
//找节点所在区域的头节点 同时进行扁平化优化,路径压缩:a->b->c->d 变成a直接指向d a->d b->d...省去中间过多不必要指向
public int find(int i){
int help_index = 0; //辅助数组索引,依次把节点往上的父节点入数组所用
//当前节点一直往上找头节点,直到找到头节点 也就是等于自身时退出
while( i != parent[i]){
help[help_index++] = i;
i = parent[i];
}
//此时退出时,i就来到了 i==parent[i]的位置,就是i节点的头节点,再将这个链上的元素依次将头节点重新赋值,直接指向头节点
//这里索引先-- 是因为当前索引已经来到头节点 本身父节点就是头节点 自身,就不用修改 后面的都修改成i
for(help_index--; help_index >= 0; help_index--){
//help[help_index]:链上的节点 该节点父节点:parent[help[help_index]] 重新指向最终的父节点i
parent[help[help_index]] = i;
}
//最后返回头节点
return i;
}
//合并
public void union(int i, int j){
//先取两节点在区域的头节点
int i1 = find(i);
int i2 = find(j);
//如果不相等,再合并
if(i1 != i2){
//判断区分出区域大小
if(size[i1] >= size[i2]){
//将小区域添加到大区域,小合并到大的意思
size[i1] += size[i2];
//小区头节点的父节点指向大区域头节点
parent[i2] = i1;
}else{
size[i2] += size[i1];
parent[i1] = i2;
}
//合并后 集合-1
set--;
}
}
//返回集合个数
public int set(){
return set;
}
}
}
六、200. 岛屿数量
package class15;
import java.util.ArrayList;
import java.util.HashMap;
import java.util.List;
import java.util.Stack;
/**
* 岛问题 https://leetcode.cn/problems/number-of-islands/?utm_source=LCUS&utm_medium=ip_redirect&utm_campaign=transfer2china
*
* 给定一个二维数组matrix,里面的值不是1就是0,
* 上、下、左、右相邻的1认为是一片岛,
* 返回matrix中岛的数量
*/
public class NumberOfIslands {
//方法一 递归方法 写法简单
public static int numIslands3(char[][] grid) {
int ans = 0;
int N = grid.length;
int M = grid[0].length;
//依次遍历每个值 然后通过递归每个元素的上下左右
for(int i = 0; i< N;i++){
for(int j = 0; j < M;j++){
if(grid[i][j] == '1'){
ans ++;
dfs(grid,i,j);
}
}
}
return ans;
}
public static void dfs(char[][]grid,int i,int j){
//越界判断,以及下次遇到的非'1'的节点就退出返回上层
if(i < 0 || i == grid.length || j < 0 || j == grid[0].length || grid[i][j] != '1'){
return;
}
//来到这里就说明符合'1' 那么就把该值改成其他值,避免后面递归回到这个位置又进行处理。陷入死循环
grid[i][j] = '2';
//分别 上下左右 递归判断 有1的就连一片的赋值2 然后退出
dfs(grid,i-1,j);
dfs(grid,i+1,j);
dfs(grid,i,j-1);
dfs(grid,i,j+1);
}
//方法二:并查集 不用哈希表 用数组来表示
public static int numIslands2(char[][] board){
int row = board.length;
int col = board[0].length;
//创建并查集对象 把原始二维数组做入参,待会遍历二维数组进行将1需要合并的合并
UnionFind2 unionFind2 = new UnionFind2(board);
//遍历每个元素的左和上 就可以覆盖全部元素,考虑第一行没有上边界 第一列没有左边界 所以分开两个for来提前处理
//遍历第一行 跳过第一个board[0][0] 从第二个开始看左边的和当前的是否都1 是就合并
for(int c = 1; c < col;c++){
if(board[0][c-1] == '1' && board[0][c] == '1'){
unionFind2.union(0,c-1,0,c);
}
}
//第一列同理
for(int r = 1; r < row;r++){
if(board[r-1][0] == '1' && board[r][0] == '1'){
unionFind2.union(r-1,0,r,0);
}
}
//处理完第一行 第一列后 剩下的就是直接 看左和上 不需要溢出判断
for(int r = 1;r < row;r++){
for(int c = 1; c < col;c++){
//当前节点和左边节点为1 合并
if(board[r][c] == '1' && board[r][c-1] == '1'){
unionFind2.union(r,c,r,c-1);
}
//当前节点和上边节点为1 合并
if(board[r][c] == '1' && board[r-1][c] == '1'){
unionFind2.union(r,c,r-1,c);
}
}
}
//遍历完,并查集中去set集合个数就是 有多少个区域
return unionFind2.set();
}
//定义并查集类
public static class UnionFind2{
public int[] parent; //节点i所在区域的父节点数组
public int[] size; //节点i所在区域的大小
public int[] help; //辅助数组,用于在找节点的头节点函数中 将该区域全部节点路径压缩 就是直接指向头节点
public int sets; //集合区域的个数
public int col; //原二维数组的列数,为了转换一位数组 比如二维数组[i][j] = 一维数组[i*col+j]
public UnionFind2(char[][] board){
int row = board.length; //行数
col = board[0].length; //列数
int len = row * col; //二维数组个数,用来转换成一维数组长度
parent = new int[len];
size = new int[len];
help = new int[len];
sets = 0;
for(int i = 0; i< row;i++){
for(int j = 0; j<col;j++){
if(board[i][j] == '1'){
int x = index(i,j);
parent[x] = x;
size[x] = 1;
sets++;
}
}
}
}
//获取二维数组的索引对应到一维数组的索引 [i][j] 转换一维数组就是 i行个元素 +j个元素
public int index(int i, int j){
return i * col + j;
}
//获取当前节点的区域头节点
public int find(int i){
int help_index = 0; //定义辅助数组索引用来遍历存放数
while(i != parent[i]){ //当前节点一直往上遍历直到找到区域头节点
help[help_index++] = i;
i = parent[i];
}
//至此i 来到该节点区域的头节点 最后返回
//返回前对该区域的全部节点的指向路劲压缩,a->b->c => a->c parent[i] =i 直接就等于实际的头节点
//help_index本身就是头节点指向自己 不用遍历 所以先--
for(help_index--;help_index>=0;help_index--){
parent[help[help_index]] = i;
}
return i;
}
//合并
public void union(int r1, int c1, int r2, int c2){
//通过index函数获取二维数组索引转换对应一维数组索引
int index1 = index(r1,c1);
int index2 = index(r2,c2);
int head1 = find(index1);
int head2 = find(index2);
if(head1 != head2){
//两个头节点不相等,那么就进行合并
//将小的区域元素都加到大的区域 并将小区域头节点指向大区域
if(size[head1] >= size[head2]){
size[head1] += size[head2];
parent[head2] = head1;
}else{
size[head2] += size[head1];
parent[head1] = head2;
}
//最后合并完,集合-1 因为小区域合并到大区域
sets--;
}
}
//获取集合大小
public int set(){
return sets;
}
}
public static int numIslands1(char[][] board) {
int row = board.length;
int col = board[0].length;
Dot[][] dots = new Dot[row][col];
List<Dot> dotList = new ArrayList<>();
for (int i = 0; i < row; i++) {
for (int j = 0; j < col; j++) {
if (board[i][j] == '1') {
dots[i][j] = new Dot();
dotList.add(dots[i][j]);
}
}
}
UnionFind1<Dot> uf = new UnionFind1<>(dotList);
for (int j = 1; j < col; j++) {
// (0,j) (0,0)跳过了 (0,1) (0,2) (0,3)
if (board[0][j - 1] == '1' && board[0][j] == '1') {
uf.union(dots[0][j - 1], dots[0][j]);
}
}
for (int i = 1; i < row; i++) {
if (board[i - 1][0] == '1' && board[i][0] == '1') {
uf.union(dots[i - 1][0], dots[i][0]);
}
}
for (int i = 1; i < row; i++) {
for (int j = 1; j < col; j++) {
if (board[i][j] == '1') {
if (board[i][j - 1] == '1') {
uf.union(dots[i][j - 1], dots[i][j]);
}
if (board[i - 1][j] == '1') {
uf.union(dots[i - 1][j], dots[i][j]);
}
}
}
}
return uf.sets();
}
public static class Dot {
}
public static class Node<V> {
V value;
public Node(V v) {
value = v;
}
}
public static class UnionFind1<V> {
public HashMap<V, Node<V>> nodes;
public HashMap<Node<V>, Node<V>> parents;
public HashMap<Node<V>, Integer> sizeMap;
public UnionFind1(List<V> values) {
nodes = new HashMap<>();
parents = new HashMap<>();
sizeMap = new HashMap<>();
for (V cur : values) {
Node<V> node = new Node<>(cur);
nodes.put(cur, node);
parents.put(node, node);
sizeMap.put(node, 1);
}
}
public Node<V> findFather(Node<V> cur) {
Stack<Node<V>> path = new Stack<>();
while (cur != parents.get(cur)) {
path.push(cur);
cur = parents.get(cur);
}
while (!path.isEmpty()) {
parents.put(path.pop(), cur);
}
return cur;
}
public void union(V a, V b) {
Node<V> aHead = findFather(nodes.get(a));
Node<V> bHead = findFather(nodes.get(b));
if (aHead != bHead) {
int aSetSize = sizeMap.get(aHead);
int bSetSize = sizeMap.get(bHead);
Node<V> big = aSetSize >= bSetSize ? aHead : bHead;
Node<V> small = big == aHead ? bHead : aHead;
parents.put(small, big);
sizeMap.put(big, aSetSize + bSetSize);
sizeMap.remove(small);
}
}
public int sets() {
return sizeMap.size();
}
}
// 为了测试
public static char[][] generateRandomMatrix(int row, int col) {
char[][] board = new char[row][col];
for (int i = 0; i < row; i++) {
for (int j = 0; j < col; j++) {
board[i][j] = Math.random() < 0.5 ? '1' : '0';
}
}
return board;
}
// 为了测试
public static char[][] copy(char[][] board) {
int row = board.length;
int col = board[0].length;
char[][] ans = new char[row][col];
for (int i = 0; i < row; i++) {
for (int j = 0; j < col; j++) {
ans[i][j] = board[i][j];
}
}
return ans;
}
// 为了测试
public static void main(String[] args) {
int row = 0;
int col = 0;
char[][] board1 = null;
char[][] board2 = null;
char[][] board3 = null;
long start = 0;
long end = 0;
row = 1000;
col = 1000;
board1 = generateRandomMatrix(row, col);
board2 = copy(board1);
board3 = copy(board1);
System.out.println("感染方法、并查集(map实现)、并查集(数组实现)的运行结果和运行时间");
System.out.println("随机生成的二维矩阵规模 : " + row + " * " + col);
start = System.currentTimeMillis();
System.out.println("感染方法的运行结果: " + numIslands3(board1));
end = System.currentTimeMillis();
System.out.println("感染方法的运行时间: " + (end - start) + " ms");
start = System.currentTimeMillis();
System.out.println("并查集(map实现)的运行结果: " + numIslands1(board2));
end = System.currentTimeMillis();
System.out.println("并查集(map实现)的运行时间: " + (end - start) + " ms");
start = System.currentTimeMillis();
System.out.println("并查集(数组实现)的运行结果: " + numIslands2(board3));
end = System.currentTimeMillis();
System.out.println("并查集(数组实现)的运行时间: " + (end - start) + " ms");
System.out.println();
row = 10000;
col = 10000;
board1 = generateRandomMatrix(row, col);
board3 = copy(board1);
System.out.println("感染方法、并查集(数组实现)的运行结果和运行时间");
System.out.println("随机生成的二维矩阵规模 : " + row + " * " + col);
start = System.currentTimeMillis();
System.out.println("感染方法的运行结果: " + numIslands3(board1));
end = System.currentTimeMillis();
System.out.println("感染方法的运行时间: " + (end - start) + " ms");
start = System.currentTimeMillis();
System.out.println("并查集(数组实现)的运行结果: " + numIslands2(board3));
end = System.currentTimeMillis();
System.out.println("并查集(数组实现)的运行时间: " + (end - start) + " ms");
}
}
七、305. Number of Islands II 岛问题扩展
package class15;
import java.util.ArrayList;
import java.util.HashMap;
import java.util.List;
/**
* // 本题为leetcode原题
* // 测试链接:https://leetcode.com/problems/number-of-islands-ii/
* // 所有方法都可以直接通过
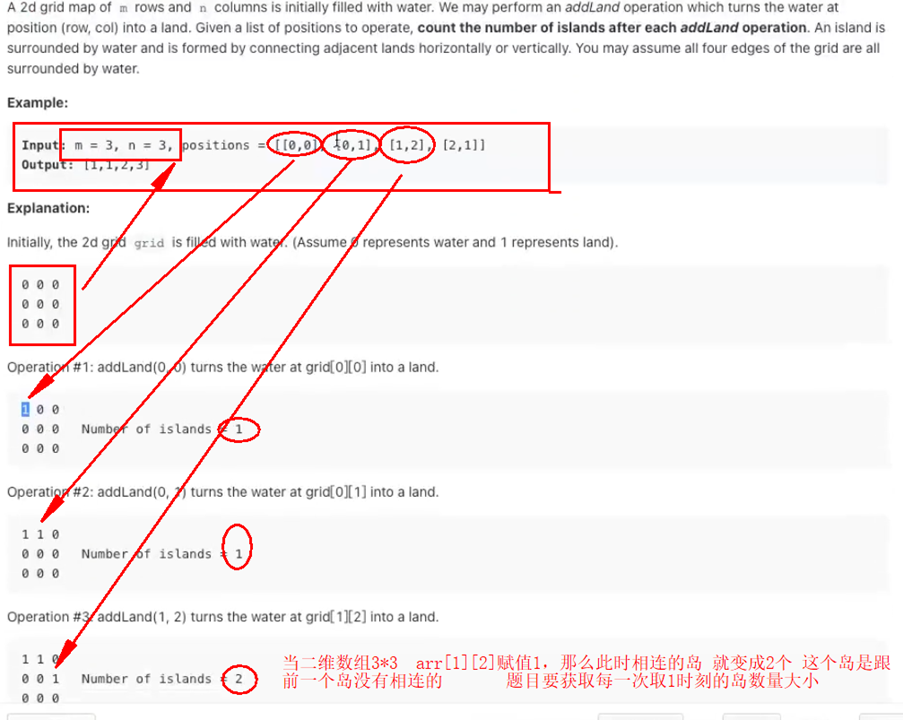
* 题意: 输入 m*n矩阵,一开始都是0,positions数组存放的就是矩阵需要赋值1的位置,返回相连1的岛数量
* 比如 3*3 矩阵
* 0 0 0
* 0 0 0
* 0 0 0
* 当前是岛数量0
* positions=[[0,0],[0,1],[1,2],[2,1]] 矩阵中依次这四个点是1
* 1.[0,0]遍历就变成
* 1 0 0
* 0 0 0
* 0 0 0 岛数量1
* <p>
* 2.[0,1]遍历
* 1 1 0
* 0 0 0
* 0 0 0 岛数量1
* <p>
* 3.[1,2]遍历
* 1 1 0
* 0 0 1
* 0 0 0 岛数量2 因为此时新添加的1 跟前面的1所在岛不相连
* <p>
* 4.[2,1]遍历
* 1 1 0
* 0 0 1
* 0 1 0 岛数量3 因为此时新添加的1 跟前面的两个岛不相连
* <p>
* 最后返回list集合[1,1,2,3]
* <p>
* <p>
* 思路:
* 并查集
*/
public class NumberOfIslandsII {
public static List<Integer> numIslands21(int m, int n, int[][] positions) {
//定义结果集合 添加每次位置进来时的岛数量
List<Integer> ans = new ArrayList<>();
//创建并查集类,参数为m n 矩阵的行列
UnionFind1 unionFind1 = new UnionFind1(m, n);
for (int[] pos : positions) {
//遍历每个位置,该位置表示1,进行并查集的连接操作,带入pos[0] pos[1]表示几行几列
ans.add(unionFind1.connect(pos[0], pos[1]));
}
return ans;
}
//定义并查集类 此时因为题目跟版本1岛数量不一样 没有一开始就把有1的给出来,而是一个一个给,并且要返回每次当前的岛数量
//所以我们类中就初步定义大小 不定义值 因为不知道1
public static class UnionFind1 {
public int[] parent; //节点所在区域的头节点
public int[] size; //头节点区域的大小
public int[] help; //辅助数组,优化路径压缩
public int set; //集合个数
public int row; //对应矩阵行数 用来定义转换一维数组索引 判断边界
public int col; //对应矩阵列数 判断边界
//入参定义矩阵行列数
public UnionFind1(int m, int n) {
//初始化确定行列数,数组长度,集合个数0
row = m;
col = n;
int len = m * n;
parent = new int[len];
size = new int[len];
help = new int[len];
set = 0;
}
//获取节点所在区域的头节点
public int find(int i) {
int help_index = 0;
//一直往上遍历直到遇到头节点
while (i != parent[i]) {
help[help_index++] = i;
i = parent[i];
}
//i来到头节点 那么就开始对该区域的全部节点重新指向到真正的头节点i
for (help_index--; help_index >= 0; help_index--) {
parent[help[help_index]] = i;
}
//最后返回i 头节点
return i;
}
//根据二维数组坐标转换对应的一位数组下标
public int index(int i, int j) {
return i * col + j;
}
//合并
public void union(int r1, int c1, int r2, int c2) {
//先判断是否越界 越界就直接退出
if (r1 == row || r1 < 0 || c1 == col || c1 < 0 || r2 == row || r2 < 0 || c2 == col || c2 < 0) {
return;
}
//不越界 就取出对应的头节点
int index1 = index(r1, c1);
int index2 = index(r2, c2);
//注意这里需要判断 是否这个头节点区域是有1的 没有1就表示没有调用connect做初始化 那就不合并,如果有1,那么size大小就是1 不是0
if (size[index1] == 0 || size[index2] == 0) {
return;
}
//接着获取各自区域的头节点
int head1 = find(index1);
int head2 = find(index2);
//都有1 说明是需要进行合并
if (head1 != head2) {
if (size[head1] >= size[head2]) {
//比较大小区,小区的大小添加到大区
size[head1] += size[head2];
//小区头节点重新指向大区头节点
parent[head2] = head1;
} else {
size[head2] += size[head1];
parent[head1] = head2;
}
//合并后set集合数量-1
set--;
}
}
//连接题目的positions数组[i][j],依次判断得到当前岛数量
public int connect(int i, int j) {
//先转换一维数组的位置索引
int index = index(i, j);
//判断如果当前索引值0,说明还没初始化,那就就行并查集
//如果为1 就表示已经初始化过,比如pos[i][j] = [2][3] 接着又是[2][3]重复的进来就不能算了
if (size[index] == 0) {
parent[index] = index; //刷新该节点的区域头节点是自身
size[index] = 1; //该节点作为头节点的区域大小赋值1
set++; //集合数量+1
}
//左右上下进行合并操作,如果四方有1的,那么就合并
union(i, j, i - 1, j);
union(i, j, i + 1, j);
union(i, j, i, j - 1);
union(i, j, i, j + 1);
//最后合并完 就返回set 表示当前岛数量
return set;
}
}
// 课上讲的如果m*n比较大,会经历很重的初始化,而k比较小,怎么优化的方法
public static List<Integer> numIslands22(int m, int n, int[][] positions) {
UnionFind2 uf = new UnionFind2();
List<Integer> ans = new ArrayList<>();
for (int[] position : positions) {
ans.add(uf.connect(position[0], position[1]));
}
return ans;
}
public static class UnionFind2 {
private HashMap<String, String> parent;
private HashMap<String, Integer> size;
private ArrayList<String> help;
private int sets;
public UnionFind2() {
parent = new HashMap<>();
size = new HashMap<>();
help = new ArrayList<>();
sets = 0;
}
private String find(String cur) {
while (!cur.equals(parent.get(cur))) {
help.add(cur);
cur = parent.get(cur);
}
for (String str : help) {
parent.put(str, cur);
}
help.clear();
return cur;
}
private void union(String s1, String s2) {
if (parent.containsKey(s1) && parent.containsKey(s2)) {
String f1 = find(s1);
String f2 = find(s2);
if (!f1.equals(f2)) {
int size1 = size.get(f1);
int size2 = size.get(f2);
String big = size1 >= size2 ? f1 : f2;
String small = big == f1 ? f2 : f1;
parent.put(small, big);
size.put(big, size1 + size2);
sets--;
}
}
}
public int connect(int r, int c) {
String key = String.valueOf(r) + "_" + String.valueOf(c);
if (!parent.containsKey(key)) {
parent.put(key, key);
size.put(key, 1);
sets++;
String up = String.valueOf(r - 1) + "_" + String.valueOf(c);
String down = String.valueOf(r + 1) + "_" + String.valueOf(c);
String left = String.valueOf(r) + "_" + String.valueOf(c - 1);
String right = String.valueOf(r) + "_" + String.valueOf(c + 1);
union(up, key);
union(down, key);
union(left, key);
union(right, key);
}
return sets;
}
}
}