Android特别的数据结构（一） SparseArray源码解析

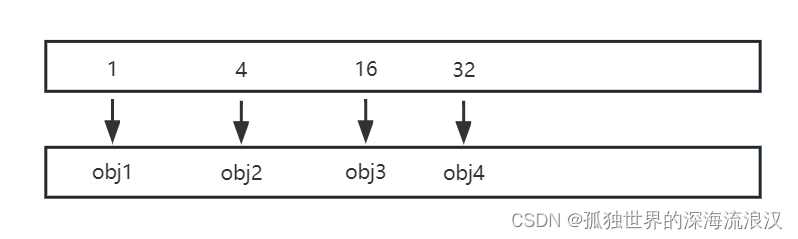
1.数据结构

class SparseArray<E> implements Cloneable

由两个数组构成，一个数组mKeys类型为int[]，存放Key，一个数组mValues类型为 E[]，存放Value。
Key数组升序排列。
默认初始容量：10
扩容：
- 如果当前长度<=4，则扩容到8
- 否则，扩容为当前长度的 2 倍
没有哈希冲突问题！因为key就是int类型数据。

请添加图片描述

2. 插入/更新

put(int key, E value)
set(int key, E value)

put() 插入语法如下

SparseArray sparseArray = new SparseArray();
sparseArray.put(4,obj2);

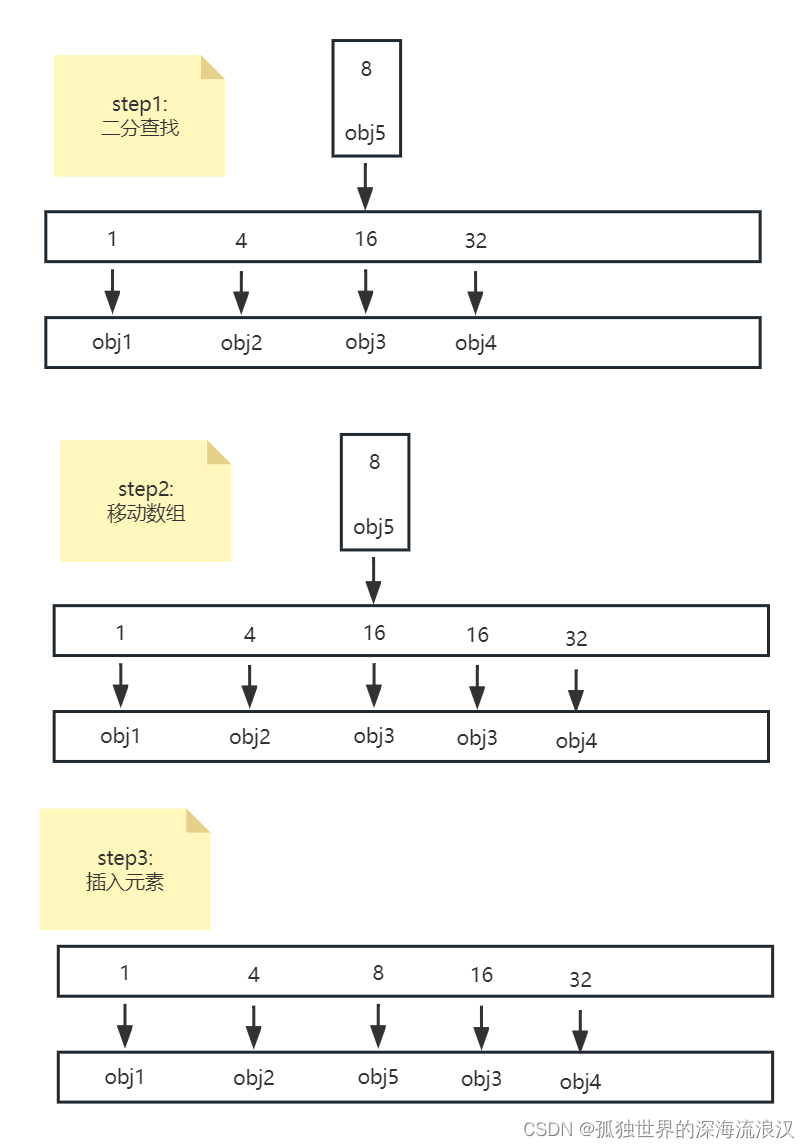
主要流程为：

二分查找key所在的位置，如果找到，则替换原有value
如果没有找到，则将后续元素平移一格，将自己插入

图示如下：

请添加图片描述

看到源码：

//添加元素
public void set(int key, E value){put(key,value);}
public void put(int key, E value) {
    //在现有的范围mSize中，二分查找key在mKeys中的下标
    //解释(1)
    int i = ContainerHelpers.binarySearch(mKeys, mSize, key);
    //由于升序二分，如果连续插入升序key，那么时间复杂度就是O(logn)
    //如果逆序插入key，那么时间复杂就是O(n)因为要平移
    if (i >= 0) {
        //如果找到了，就覆盖，因为key只为integer，所以不存在hash冲突
        mValues[i] = value;
    } else {
        //如果没找到
        //包括符号位按位取反，拿到的是二分搜索最后的lo值
        //解释(1)
        i = ~i;
        //如果lo值对应的value是DELETED，就直接填入
        //解释(2)
        if (i < mSize && mValues[i] == DELETED) {
            mKeys[i] = key;
            mValues[i] = value;
            return;
        }
        //如果lo值位置已经被占用了,在平移数组并插入元素之前，先清理废弃的下标
        //解释(3)
        if (mGarbage && mSize >= mKeys.length) {
            //先清理一下数组
            gc();
            //然后重新计算新的lo位置
            i = ~ContainerHelpers.binarySearch(mKeys, mSize, key);
        }
        //维护Key的升序！！！key数组没有内部碎片！！！（数组平移->整理）
        //安全插入，可能出现扩容和数组元素平移
        //解释(4)
        mKeys = GrowingArrayUtils.insert(mKeys, mSize, i, key);
        mValues = GrowingArrayUtils.insert(mValues, mSize, i, value);
        //添加完成
        mSize++;
    }
}

解释(1)

过程中，通过ContainerHelpers进行二分查找，通过GrowingArrayUtils进行元素插入。我们先来看到ContainerHelpers，它的工作原理就是我们熟知的二分查找：

如果mid的值就是要找的，返回mid
否则更新low、high两个指针的值，继续二分查找
如果最后都找不到，返回一个负数

//ContainerHelpers
static int binarySearch(int[] array, int size, int value) {
    int lo = 0;
    int hi = size - 1;

    while (lo <= hi) {
        // >>>1相当于 除以2
        final int mid = (lo + hi) >>> 1;
        final int midVal = array[mid];

        if (midVal < value) {
            lo = mid + 1;
        } else if (midVal > value) {
            hi = mid - 1;
        } else {
            return mid;  // value found
        }
    }
    //如果最后都找不到，返回一个负数
    return ~lo;  // value not present
}

与平时写的二分查找几乎一样，但是返回的是~lo，这是对lo的值按位取反。由于lo逻辑上保证了值为正数，所以~lo一定是负数，满足了没有查找到的返回负数的约定。但由于我们还需要在原先找的最后一个位置进行插入，所以需要复用lo的值，后续只需要再进行一次 ~ 按位取反运算即可，即 lo = ~~lo

解释(2)

如果找到的下标存的value是DELETED，说明这个位置可以直接替换为新的值，而不需要先清理空下标，再平移元素，再插入新值。

public class SparseArray<E> implements Cloneable {
    private static final Object DELETED = new Object();
    public void delete(int key){
        //让key对应的value置为 DELETED
        //...
        mValues[i] = DELETED;
        //提示下次插入的时候调整数组结构
        mGarbage = true;
    }
}

解释(3)

如果需要插入的位置被占用，就只能先平移数组，然后再把自己插入。在此之前，数组中可能存在上述DELETED节点（如果mGarbage为真），所以要先通过gc()清理，然后重新计算插入位置i，再进行数组平移和元素插入。

public class SparseArray<E> implements Cloneable {
    //目的是用来清理那些被删掉的value的节点 （标记-整理 算法）
    //思路类似移动零，把后续有用的值往前整理
    private void gc() {
        int n = mSize;
        //整理来到了第几个下标
        int o = 0;
        int[] keys = mKeys;
        Object[] values = mValues;
		//遍历一轮
        for (int i = 0; i < n; i++) {
            Object val = values[i];
			//找到value为DELETED的位置
            if (val != DELETED) {
                if (i != o) {
                    //整理
                    keys[o] = keys[i];
                    values[o] = val;
                    //将用不到的置空，去掉强引用
                    values[i] = null;
                }
                o++;
            }
        }
        //整理完成
        mGarbage = false;
        //最后o所到达的下标为所有可用数据的最大下标，此后的key都是无用的，且value全都被置空
        mSize = o;
    }
}

上述代码可以参考 leetcode-移动零的算法设计，用o来表示：后续可用的元素要整理到的下标。

解释(4)

真正要插入元素了，需要先将数组进行移动，这也是SparseArray时间复杂度O(N)的问题来源，二分查找复杂度为O(N)，但移动元素的平均时间复杂度就是数组插入元素的时间复杂度O(N)。对于mKeys和mValues的处理是一样的，主要流程为：

如果移动后不会越界，就移动，然后插入新的值
如果会越界，需要先进行扩容，然后拷贝元素到新数组，再插入新的值。

//GrowingArrayUtils
public static <T> T[] insert(T[] array, int currentSize, int index, T element) {
    //如果在原来的数组中还能放得下
    assert currentSize <= array.length;
    //看看能否将lo+1位置以后的内容全都右移一个单元
    if (currentSize + 1 <= array.length) {
        System.arraycopy(array, index, array, index + 1, currentSize - index);
        //然后将当前的值填入
        array[index] = element;
        return array;
    }
    //如果已经放不下了，只能申请一块扩容后的一块空间
    //将原来的内容拷贝到新的，同时将element插入

    //暂且认为是让VM虚拟机创建了一个新的数组
    @SuppressWarnings("unchecked")
    T[] newArray = ArrayUtils.newUnpaddedArray((Class<T>)array.getClass().getComponentType(),growSize(currentSize));
    //扩容复制前半部分
    System.arraycopy(array, 0, newArray, 0, index);
    //插入新值
    newArray[index] = element;
    //拷贝剩余部分
    System.arraycopy(array, index, newArray, index + 1, array.length - index);
    return newArray;
}

//扩容：
public static int growSize(int currentSize) {
    return currentSize <= 4 ? 8 : currentSize * 2;
}

3. 插入/更新元素

append(int key, E value)

假设当前SparseArray内容如下：

请添加图片描述

如果我要插入的key为40（大于已存在的最大key），直接加在最后就好了，时间复杂度为O(1)，但如果按照 put() 的设计，要先二分查找，找到新的mKeys中的位置为index=4，时间复杂度为O(logN)。

大多数情况，我们的Key总是几乎升序的，在这种情况下，总使用put()效率自然底下，所以通过append()，加快升序Key数据的添加。

特别的，如果Key为升序Integer类型，SparseArray的性能比HashMap要好，不论是运行时间还是内存占用。

//SparseArray
//用这个方法来插入key升序数据，时间复杂度为O(1)
//用put()插入key升序的数据，时间复杂度为O(logn)
public void append(int key, E value) {
    //如果原先数组有数据了，而且 key 并不是最大的，就正常put
    if (mSize != 0 && key <= mKeys[mSize - 1]) {
        put(key, value);
        return;
    }
    //如果原先数组是空的，或者key超过了已有key的最大值，
    // 那么就可以在mSize的位置直接拼接，没必要再去二分一趟

    //如果mSize没更新，gc整理一下数组
    if (mGarbage && mSize >= mKeys.length) {
        gc();
    }
    //直接将数据填在数组的最后
    mKeys = GrowingArrayUtils.append(mKeys, mSize, key);
    mValues = GrowingArrayUtils.append(mValues, mSize, value);
    //更新mSize
    mSize++;
}

其中，由GrowingArrayUtils来执行真正的append()逻辑，可能需要扩容：

//GrowingArrayUtils
public static <T> T[] append(T[] array, int currentSize, T element) {
    if (currentSize + 1 > array.length) {
        @SuppressWarnings("unchecked")
        //扩容
        T[] newArray = ArrayUtils.newUnpaddedArray(
            (Class<T>) array.getClass().getComponentType(), growSize(currentSize));
        System.arraycopy(array, 0, newArray, 0, currentSize);
        array = newArray;
    }
    //如果要扩容先扩容
    //然后直接在最后位置添加新元素
    array[currentSize] = element;
    return array;
}

4. 查找元素

get(int key)
get(int key, E valueIfKeyNotFound)

这个就简单了，就是二分查找，时间复杂度为O(logN)，如果找到的value不是DELETED，就返回，否则返回null，或者默认值：

//SparseArray<E>
public E get(int key) {
    return get(key, null);
}
//如果没找到，可以给一个默认值，类似getOrDefault()的设计。
public E get(int key, E valueIfKeyNotFound) {
    //一样也是先二分查找，找到下标位置
    int i = ContainerHelpers.binarySearch(mKeys, mSize, key);
    //如果没找到，或者这个位置的元素以及被删除了
    if (i < 0 || mValues[i] == DELETED) {
        return valueIfKeyNotFound;
    } else {
        //下标找到了，值也可以用，算是找到了
        return (E) mValues[i];
    }
}

5. 查找排序第index位的Key值

int keyAt(int index)

我们知道SparseArray维护的mKeys是升序数组，除了为本身逻辑提供二分查找，也为用户提供了key升序的特性，可以直接拿到第i小，第k大的元素。

//key是升序的，拿到排在第index的key
public int keyAt(int index) {
    if (index >= mSize && UtilConfig.sThrowExceptionForUpperArrayOutOfBounds) {

        throw new ArrayIndexOutOfBoundsException(index);
    }
    //除了删除操作，都要判断是否需要整理数组
    if (mGarbage) {
        gc();
    }

    return mKeys[index];
}

6. 查找对应Value所在的位置

int indexOfValueByValue(E value)

就是O(N)的遍历查找，查看目标Value所在的下标，如果没找到就返回-1

//SparseArray
public int indexOfValueByValue(E value) {
    //除了删除，都需要尝试整理数组
    if (mGarbage) {
        gc();
    }
	//遍历
    for (int i = 0; i < mSize; i++) {
        //允许value为null，所以要先做null的判断
        if (value == null) {
            if (mValues[i] == null) {
                return i;
            }
        } else {
            //如果value不为null，再去用equals()来判断
            if (value.equals(mValues[i])) {
                return i;
            }
        }
    }
    return -1;
}

SparseArray允许value为null，所以要先对null做判断，如果不为null，才尝试equals()比较，这和HashMap对null元素的判断设计一致。

7. 删除元素

remove(int key)
delete(int key)

这个我们在前面将 DELETED value的时候也提到了delete()的主要任务，我们来看一下源码：

//SparseArray
private static final Object DELETED = new Object();
private boolean mGarbage = false;

public void remove(int key) {
    delete(key);
}
public void delete(int key) {
    //一样也是先二分查找，找到下标位置
    int i = ContainerHelpers.binarySearch(mKeys, mSize, key);

    if (i >= 0) {
        //并不是直接置空，也不调整结构，只有下次要用的时候才去调整，提高效率
        if (mValues[i] != DELETED) {
            //标记为DELETED
            mValues[i] = DELETED;
            //提示下次插入的时候调整数组结构
            mGarbage = true;
        }
    }
}

为了兼容不同程序员对“删除”操作命名的习惯，设计为remove()和delete()的作用一样。

8. 删除元素并返回原值

E removeReturnOld(int key)

和删除的逻辑一致，不过在将mValue[i]=DELETED之前，将原来的值记录下来，用于返回。

//SparseArray.java
public E removeReturnOld(int key) {
    //不仅delete，还把原有的值返回出去，如果存在的话
    int i = ContainerHelpers.binarySearch(mKeys, mSize, key);
	//如果找到了要删除元素的下标
    if (i >= 0) {
        if (mValues[i] != DELETED) {
            //将原有的值记录
            final E old = (E) mValues[i];
            //将value置为DELETED这个对象
            mValues[i] = DELETED;
            //通知下次插入、查找操作的时候先进行整理
            mGarbage = true;
            //返回原有的值
            return old;
        }
    }
    //如果要删除的元素不存在，直接return null
    return null;
}

9. 删除排序第index位的元素

removeAt(int index)

我们知道，在SparseArray的mKeys中，所有已插入的key是按升序排列的，这设计初衷是为了配合二分查找，但也为我们的业务提供了方便，类似TreeMap，它提供了按Key排序的插入！

//SparseArray
//删除按key排序为index位置上的元素
public void removeAt(int index) {
    //越界检查
    if (index >= mSize && UtilConfig.sThrowExceptionForUpperArrayOutOfBounds) {
        throw new ArrayIndexOutOfBoundsException(index);
    }
    //SparseArray中的删除就是把value置为DELETED，并将mGarbage标志置为true
    if (mValues[index] != DELETED) {
        mValues[index] = DELETED;
        mGarbage = true;
    }
}

10. 批量删除

removeAtRange(int index, int size)

可以删除排序第index位以及接连着的size个数的元素

//SparseArray
public void removeAtRange(int index, int size) {
    //为了不越界，最后一个index为mSize和 index+size的最小值
    final int end = Math.min(mSize, index + size);
    for (int i = index; i < end; i++) {
        removeAt(i);
    }
}

总结

SparseArray与HashMap/TreeMap对比，表中说明只针对SparseArray

任务	SparseArray	说明	HashMap	TreeMap
删除	O(logN)	二分查找，置DELETED	O(1)	O(logN)
顺序插入	O(1) or O(N)	O(1)原因：append()直接放在最后可能扩容 O(N)原因：可能需要整理数组gc()	O(1)	O(logN)
随机插入	O(logN) or O(N)	O(logN)：二分查找插入位置 O(N)；可能需要整理数组gc() O(N)：插入前可能需要移动数组元素	O(1)	O(logN)
倒序插入	O(N)	O(logN):二分查找插入位置 O(N)：一定需要移动数组元素	O(1)	O(logN)
查找	O(logN)	二分查找	O(1)	O(logN)
查找排序为index的Key	O(1)+O(N)	O(1)直接index索引 O(N)：可能需要整理数组gc()	结合API自行实现	结合API自行实现

同样KeyValue类型时，几乎只有一半的内存占用：SparseArray = 1/2 HashMap

这个也挺好理解的，假设有N个元素，大概来测算一下：

//TreeMap
Entry<K,V> root;// 21 * N Byte
class Entry<K,V>{//至少21 Byte
    K key;//4 Byte
    V value;//4 Byte
    Entry<K,V> left;//4 Byte
    Entry<K,V> right;//4 Byte
    Entry<K,V> parent;//4 Byte
    boolean color = BLACK;//1 Byte
}
//HashMap
Node<K,V>[] table;//16 * N Byte
class Node<K,V>{//至少16 Byte
    final int hash;//4 Byte
    final K key;//4 Byte
    V value;//4 Byte
    Node<K,V> next;//4 Byte
}
//SparseArray
int[] mKeys;//4 * N Byte
Object[] mValues;//4 * N Byte