1. 铜中电子的速度

信号在传输线上传输的速度有多快？如果人们经常错误地认为信号在传输线上的速度取决于导线中电子的速度。凭着这种错误的直觉，我们可能会想象降低互连的电阻会提高信号的速度。事实上，典型铜线中电子的速度实际上比信号速度慢约 100 亿倍。

估算铜线中电子的速度很容易。假设我们有一根粗略的 18 号圆线，直径 1 毫米，电流为 1 安培。我们可以根据每秒有多少电子通过一段导线、导线中电子的密度和导线的横截面积来计算导线中电子的速度。导线中的电流可以表示为：

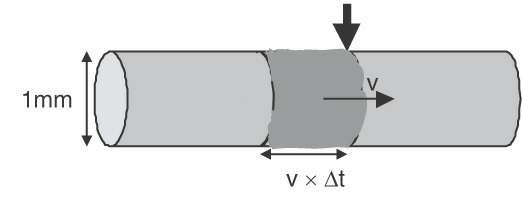
从7-1我们可以计算出电子的电压：

其中I表示通过某一点的电流，以安培表示；△Q表示在一个时间间隔内流动的电荷，以库仑为单位;△t表示时间间隔；q表示一个电子的电荷，等于1.6x10负十九次方库仑；n表示自由电子的密度，以/m三次方为单位；A表示导线横截面面积；v表示导线中的电子移动速度，单位m/s。

每个铜原子贡献大约两个可以穿过导​​线的自由电子。铜原子之间的距离约为 1 nm。这使得自由电子的密度 n 约为 n ∼ 10的27次方每平方米。

对于直径为 1 mm 的导线，横截面积约为 A ∼ 10的-6次方平方米。结合这些术语并在导线中使用 1 安培电流，导线中电子的速度可粗略估算为：

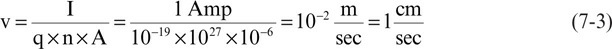
电子以大约 1 厘米/秒的速度行进。这大约和一只蚂蚁在地上奔跑一样快。

通过这个简单的分析，我们看到电子在导线中的速度与空气中的光速相比非常慢。导线中电子的速度实际上与信号的速度无关。同样，正如我们将看到的，电线的电阻对传输线中信号的速度只有非常小的、几乎无关紧要的影响。只有在极端情况下，互连的电阻才会影响信号速度——即便如此，影响也非常小。我们必须从错误的观念中重新校准我们的直觉，即较低的电阻意味着更快的信号。

但是我们如何调和信号的速度与电线中电子的极慢速度呢？信号如何在比电子从一端到达另一端所需的时间短得多的时间内从导线的一端到达另一端？答案在于电子之间的相互作用。

如果我们有一个装满弹珠的管子，将一颗弹珠从一端推入，另一端几乎是瞬间就会出现另一颗弹珠。弹珠之间的相互作用——一个弹珠对下一个弹珠的力——从弹珠传递到弹珠的速度比弹珠的实际速度快得多。

当火车停在十字路口并再次启动时，车厢之间的联轴器与火车的接合速度比机车向前移动的速度快得多。以同样的方式，当导线中的一个电子被源抖动时，它通过它们之间的电场与相邻电子的相互作用也会抖动。电场中的这种扭结以变化场允许的光速传播到下一个电子。

当电线一端的电子移动时，电场中的扭结传播到下一个电子，并且该电子移动，在其电场中产生扭结到下一个电子，并一直沿着链向下直到最后一个电子电子从另一端移出电线。相互作用的速度——电子之间电场的扭结——决定了信号传播的速度，而不是电子本身的速度。

2. 传输线中信号的速度

如果电子速度并不决定信号的速度，那么信号的速度由谁决定呢？

信号的速度取决于导体周围的材料以及与信号相关的不断变化的电场和磁场在传输线导体周围的空间中建立和传播的速度。

下图展示了信号在传输线上传播的最简单方式。信号是信号路径和返回路径之间的传播电压差。伴随着信号的传播，在两个导体之间会产生电压差，伴随电压差的是导体之间的电场。

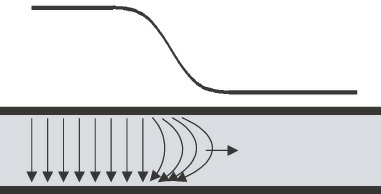
信号在传输线传输的过程中产生电场，信号的速度取决于在信号和返回路径导体之间能够产生多快的变化的电磁场。

除了电压之外，信号导体和返回导体中还必须有电流流动，以提供电荷来为导体充电，从而得到产生电场的电压差。穿过导体的电流回路会产生磁场。

只需将电池的引线接触信号和返回路径，即可将信号发射到传输线中。突然的电压变化会产生突然的电场和磁场变化。这种场扭结将以变化的电场和磁场的速度（即材料中的光速）传播通过传输线周围的介电材料。

我们通常认为光是我们可以看到的电磁辐射。然而，所有变化的电磁场都是完全相同的，并且由完全相同的一组方程式麦克斯韦方程组描述。唯一的区别是波的频率。对于可见光，频率约为 1,000,000GHz。对于高速数字产品中常见的信号，频率约为 1–10 GHz。

电磁场建立的快慢会决定信号的速度。电磁场的传播和相互作用可以用麦克斯韦方程组来描述，如果电场和磁场发生变化，它们产生的扭结将以取决于某些常数和材料特性的速度向外传播。变化速度见下式：

其中，

表示自由空间的介电常数，8.89x10的-12次方F/m

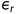表示材料的相对介电常数

表示自由空间的渗透性，4πx10的-7次方H/m

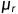表示材料的相对渗透性

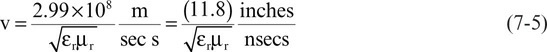
在空气中，相对介电常数和相对渗透性都是1，所以光速大约12inch/s。

对于几乎所有互连材料，电介质的磁导率 μ 为 1。所有不含铁磁材料的聚合物的磁导率为 1。因此，可以忽略该项。相比之下，材料的相对介电常数 ε 绝不会小于或等于 1，空气除外。在所有真实的互连材料中，介电常数都大于 1。这意味着互连中的光速将始终小于 12 英寸/纳秒。速度是：

为简洁起见，我们通常将相对介电常数简称为“介电常数”。这个数字表征了绝缘体的一些电气特性。它是一个重要的电性能。对于大多数聚合物，它大约为 4。对于玻璃，它约为 6，而对于陶瓷，它约为 10。

在某些材料中，介电常数可能随频率变化。换句话说，材料中的光速可能与频率有关。我们称这种特性色散为频率对材料中光速的依赖性。通常，介电常数随频率升高而降低。当我们走向更高的频率时，这使得材料中的光速增加。在大多数应用中，色散很小，可以忽略不计。

在大多数常见材料中，例如 FR4，介电常数在 500 MHz 至 10 GHz 范围内变化很小。根据环氧树脂与玻璃纤维的比例，FR4 的介电常数可以从 3.5 到 4.5。大多数互连层压板材料的介电常数约为 4。这表明了一个简单易记的概括。

要记住的一个很好的经验法则是，大多数互连中的光速约为 12 英寸/纳秒/sqrt(4) = 6 英寸/纳秒。

在评估板级互连中的信号速度时，我们可以假设它们以大约 6 英寸/纳秒的速度传播。

当场线看到介电材料的组合时，例如微带线，其中一些场线在大块材料中，一些在上方的空气中，影响信号速度的有效介电常数是不同材料的组合。当材料在整个横截面上不均匀时，预测有效介电常数的唯一方法是使用 2D 场解算器。例如，在带状线的情况下，所有场都看到相同的材料，有效介电常数是体介电常数。

互连的时间延迟、TD 和长度通过以下方式相关：

这意味着，例如，在 FR4 中向下传输 6 英寸长的互连，时间延迟约为 6 英寸/6 英寸/纳秒，或约 1 纳秒。行进 12 英寸大约需要 2 纳秒。

布线延迟，即每英寸互连延迟的皮秒数，也是一个有用的指标。它只是速度的倒数：1/v。对于 FR4，布线延迟约为 1/6 英寸/纳秒 = 0.166 纳秒/英寸，或 170 皮秒/英寸。这是在 FR4 中沿着传输线传播的信号的每英寸延迟。每英寸互连都有 170 皮秒的传播延迟。通过 0.5 英寸 BGA 引线的总延迟为 170 皮秒/英寸 × 0.5 英寸 = 85 皮秒。