1599. 经营摩天轮的最大利润

题目描述

你正在经营一座摩天轮，该摩天轮共有 4 个座舱，每个座舱最多可以容纳 4 位游客。你可以逆时针轮转座舱，但每次轮转都需要支付一定的运行成本 runningCost 。摩天轮每次轮转都恰好转动 1 / 4 周。

给你一个长度为 n 的数组 customers ， customers[i] 是在第 i 次轮转（下标从 0 开始）之前到达的新游客的数量。这也意味着你必须在新游客到来前轮转 i 次。每位游客在登上离地面最近的座舱前都会支付登舱成本 boardingCost ，一旦该座舱再次抵达地面，他们就会离开座舱结束游玩。

你可以随时停下摩天轮，即便是在服务所有游客之前。如果你决定停止运营摩天轮，为了保证所有游客安全着陆，将免费进行所有后续轮转。注意，如果有超过 4 位游客在等摩天轮，那么只有 4 位游客可以登上摩天轮，其余的需要等待下一次轮转。

返回最大化利润所需执行的最小轮转次数。如果不存在利润为正的方案，则返回 -1 。

示例 1

在这里插入图片描述

输入：customers = [8,3], boardingCost = 5, runningCost = 6
输出：3
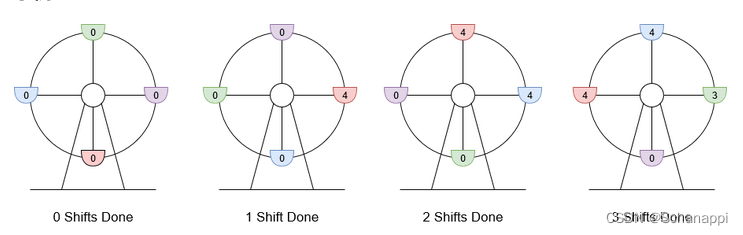
解释：座舱上标注的数字是该座舱的当前游客数。

8 位游客抵达，4 位登舱，4 位等待下一舱，摩天轮轮转。当前利润为 4 * $5 - 1 * $6 = $14 。
3 位游客抵达，4 位在等待的游客登舱，其他 3 位等待，摩天轮轮转。当前利润为 8 * $5 - 2 * $6 = $28 。
最后 3 位游客登舱，摩天轮轮转。当前利润为 11 * $5 - 3 * $6 = $37 。
轮转 3 次得到最大利润，最大利润为 $37 。

示例 2

输入：customers = [10,9,6], boardingCost = 6, runningCost = 4
输出：7
解释：

10 位游客抵达，4 位登舱，6 位等待下一舱，摩天轮轮转。当前利润为 4 * $6 - 1 * $4 = $20 。
9 位游客抵达，4 位登舱，11 位等待（2 位是先前就在等待的，9 位新加入等待的），摩天轮轮转。当前利润为 8 * $6 - 2 * $4 = $40 。
最后 6 位游客抵达，4 位登舱，13 位等待，摩天轮轮转。当前利润为 12 * $6 - 3 * $4 = $60 。
4 位登舱，9 位等待，摩天轮轮转。当前利润为 * $6 - 4 * $4 = $80 。
4 位登舱，5 位等待，摩天轮轮转。当前利润为 20 * $6 - 5 * $4 = $100 。
4 位登舱，1 位等待，摩天轮轮转。当前利润为 24 * $6 - 6 * $4 = $120 。
1 位登舱，摩天轮轮转。当前利润为 25 * $6 - 7 * $4 = $122 。
轮转 7 次得到最大利润，最大利润为$122 。

示例 3

输入：customers = [3,4,0,5,1], boardingCost = 1, runningCost = 92
输出：-1
解释：

3 位游客抵达，3 位登舱，0 位等待，摩天轮轮转。当前利润为 3 * $1 - 1 * $92 = -$89 。
4 位游客抵达，4 位登舱，0 位等待，摩天轮轮转。当前利润为 is 7 * $1 - 2 * $92 = -$177 。
0 位游客抵达，0 位登舱，0 位等待，摩天轮轮转。当前利润为 7 * $1 - 3 * $92 = -$269 。
5 位游客抵达，4 位登舱，1 位等待，摩天轮轮转。当前利润为 12 * $1 - 4 * $92 = -$356 。
1 位游客抵达，2 位登舱，0 位等待，摩天轮轮转。当前利润为 13 * $1 - 5 * $92 = -$447 。
利润永不为正，所以返回 -1 。

提示

n == customers.length
1 <= n <= 105
0 <= customers[i] <= 50
1 <= boardingCost, runningCost <= 100

算法一：模拟

思路

模拟摩天轮的运行情况，每次轮转时，累加等待游客以及新到达的游客，每次只允许最多 4 个人上舱，计算当前利润，考虑是否更新最大利润和对应的轮次，并更新等待的游客数量。

收获

合并考虑两种情况

我一开始的想法是，先遍历 customer.size() 的轮次，接着遍历剩余未上舱的 customer ，分成两个循环考虑。但其实两部分代码差不多，完全可以合并考虑。
```
for(int i=0; i<customers.size() || wait>0; ++i)
	wait += i<customers.size()? customers[i] : 0;
```
对于每次上舱的人数也可以合并考虑，如int up = min(4, wait); ，我分成了两个 if 语句，显得很繁琐；
对于利润最大的轮次，直接进行保存，如果后续有利润更高的情况，直接覆盖 ans 即可； ans = i+1;
题解中 wait 的考虑也很巧妙， wait += i<customers.size()? customers[i] : 0;

算法情况

时间复杂度：O（s/4），其中 s 为 customer 的总和；
空间复杂度：O（1）；

代码

class Solution {
public:
    int minOperationsMaxProfit(vector<int>& customers, int boardingCost, int runningCost) {
        if(boardingCost * 4 <= runningCost) return -1;
        int ans = 0;
        // 目前在排队的顾客数
        int wait = 0;
        int profit = 0, maxProfit = 0;
        for(int i=0; i<customers.size() || wait>0; ++i){
            wait += i<customers.size()? customers[i] : 0;
            int up = min(4, wait); // 计算此轮能上舱的人数
            profit += boardingCost * up - runningCost; // 计算当前利润
            if(profit > maxProfit){ // 更新最大利润
                maxProfit = profit;  
                ans = i+1;  // ans 表示最大利润的轮次
            } 
            wait -= up;
        }
        return ans == 0 ? -1 : ans;
    }
};