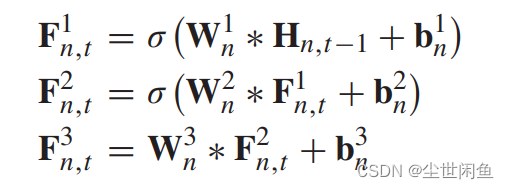深度学习笔记：数据正规化和抑制过拟合

1 Batch-normalization

batch-normalization将输入数据转化为平均值0，标准差为1的分布，该方法可以加速学习并抑制过拟合。batch-normalization作为神经网络特定的一个层出现

batch-normalization计算表达式：
在这里插入图片描述
接下来，会对数据进行一定的缩放和平移，得到y = γx + β，其中γ和β为参数，初始值为1和0，会根据学习更新

batch-normalization计算图表示：
在这里插入图片描述
比较batch-normalization对训练准确度影响：

# coding: utf-8
import sys, os
sys.path.append("D:\AI learning source code")  # 为了导入父目录的文件而进行的设定
import numpy as np
import matplotlib.pyplot as plt
from dataset.mnist import load_mnist
from common.multi_layer_net_extend import MultiLayerNetExtend
from common.optimizer import SGD, Adam

(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True)

# 减少学习数据
x_train = x_train[:1000]
t_train = t_train[:1000]

max_epochs = 20
train_size = x_train.shape[0]
batch_size = 100
learning_rate = 0.01


def __train(weight_init_std):
    bn_network = MultiLayerNetExtend(input_size=784, hidden_size_list=[100, 100, 100, 100, 100], output_size=10, 
                                    weight_init_std=weight_init_std, use_batchnorm=True)
    network = MultiLayerNetExtend(input_size=784, hidden_size_list=[100, 100, 100, 100, 100], output_size=10,
                                weight_init_std=weight_init_std)
    optimizer = SGD(lr=learning_rate)
    
    train_acc_list = []
    bn_train_acc_list = []
    
    iter_per_epoch = max(train_size / batch_size, 1)
    epoch_cnt = 0
    
    for i in range(1000000000):
        batch_mask = np.random.choice(train_size, batch_size)
        x_batch = x_train[batch_mask]
        t_batch = t_train[batch_mask]
    
        for _network in (bn_network, network):
            grads = _network.gradient(x_batch, t_batch)
            optimizer.update(_network.params, grads)
    
        if i % iter_per_epoch == 0:
            train_acc = network.accuracy(x_train, t_train)
            bn_train_acc = bn_network.accuracy(x_train, t_train)
            train_acc_list.append(train_acc)
            bn_train_acc_list.append(bn_train_acc)
    
            print("epoch:" + str(epoch_cnt) + " | " + str(train_acc) + " - " + str(bn_train_acc))
    
            epoch_cnt += 1
            if epoch_cnt >= max_epochs:
                break
                
    return train_acc_list, bn_train_acc_list


# 3.绘制图形==========
weight_scale_list = np.logspace(0, -4, num=16)
x = np.arange(max_epochs)

for i, w in enumerate(weight_scale_list):
    print( "============== " + str(i+1) + "/16" + " ==============")
    train_acc_list, bn_train_acc_list = __train(w)
    
    plt.subplot(4,4,i+1)
    plt.title("W:" + str(w))
    if i == 15:
        plt.plot(x, bn_train_acc_list, label='Batch Normalization', markevery=2)
        plt.plot(x, train_acc_list, linestyle = "--", label='Normal(without BatchNorm)', markevery=2)
    else:
        plt.plot(x, bn_train_acc_list, markevery=2)
        plt.plot(x, train_acc_list, linestyle="--", markevery=2)

    plt.ylim(0, 1.0)
    if i % 4:
        plt.yticks([])
    else:
        plt.ylabel("accuracy")
    if i < 12:
        plt.xticks([])
    else:
        plt.xlabel("epochs")
    plt.legend(loc='lower right')
    
plt.show()

在该程序中，我们使用mnist数据集训练两个6层神经网络（5个隐藏层，每层100个神经元），其中一个网络使用batch-normalization，另一个不使用。两个网络权重更新方法均为SGD，学习率均为0.01。

每一个epoch中，我们随机抽取mnist数据集100个数据作为训练样本。每20个epoch将两个网络训练结果绘制成图象，并开启下一轮实验，一共进行16轮实验，比较使用batch-normalization和不使用的识别准确率区别。

实验结果：
在这里插入图片描述
可以看出在大多数情况，使用batch-normalization（蓝色实线）训练效果远强于不使用（橙色虚线）。

过拟合

过拟合指神经网络对于训练数据预测准确率高，但对测试数据准确率低的情况。为了提高网络的泛化能力，我们需要抑制过拟合。

过拟合出现条件：
1 训练样本量过少，没有涵盖多样的数据
2 神经网络层数太多，导致表现力过强，容易和训练数据过拟合

过拟合状况复现：

# coding: utf-8
import os
import sys

sys.path.append("D:\AI learning source code")  # 为了导入父目录的文件而进行的设定
import numpy as np
import matplotlib.pyplot as plt
from dataset.mnist import load_mnist
from common.multi_layer_net import MultiLayerNet
from common.optimizer import SGD

(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True)

# 为了再现过拟合，减少学习数据
x_train = x_train[:300]
t_train = t_train[:300]

# weight decay（权值衰减）的设定 =======================
weight_decay_lambda = 0 # 不使用权值衰减的情况
# weight_decay_lambda = 0.1
# ====================================================

network = MultiLayerNet(input_size=784, hidden_size_list=[100, 100, 100, 100, 100, 100], output_size=10,
                        weight_decay_lambda=weight_decay_lambda)
optimizer = SGD(lr=0.01)

max_epochs = 201
train_size = x_train.shape[0]
batch_size = 100

train_loss_list = []
train_acc_list = []
test_acc_list = []

iter_per_epoch = max(train_size / batch_size, 1)
epoch_cnt = 0

for i in range(1000000000):
    batch_mask = np.random.choice(train_size, batch_size)
    x_batch = x_train[batch_mask]
    t_batch = t_train[batch_mask]

    grads = network.gradient(x_batch, t_batch)
    optimizer.update(network.params, grads)

    if i % iter_per_epoch == 0:
        train_acc = network.accuracy(x_train, t_train)
        test_acc = network.accuracy(x_test, t_test)
        train_acc_list.append(train_acc)
        test_acc_list.append(test_acc)

        print("epoch:" + str(epoch_cnt) + ", train acc:" + str(train_acc) + ", test acc:" + str(test_acc))

        epoch_cnt += 1
        if epoch_cnt >= max_epochs:
            break


# 3.绘制图形==========
markers = {'train': 'o', 'test': 's'}
x = np.arange(max_epochs)
plt.plot(x, train_acc_list, marker='o', label='train', markevery=10)
plt.plot(x, test_acc_list, marker='s', label='test', markevery=10)
plt.xlabel("epochs")
plt.ylabel("accuracy")
plt.ylim(0, 1.0)
plt.legend(loc='lower right')
plt.show()

在该程序中，我们为了模拟过拟合现象，使用300的样本量，和7层神经网络（6个隐藏层，每次神经元个数100），进行200个epoch训练，并绘制训练准确度和测试准确度图象

实验结果：
在这里插入图片描述
可以看到神经网络对训练数据集拟合度非常高，在后期直接达到1（对每个epoch中300个数据预测完全正确），但是对测试数据集准确度较低，并在后期没有增长，这就是过拟合的现象。

权值衰减

权值衰减是一种抑制过拟合的方法。一般来说，过大的权重值是导致过拟合的原因。权值衰减的原理是在损失函数上加上权重的L2范数作为对过大权重值“惩罚”。由于神经网络学习的目的是降低损失函数的值，对损失函数加上关于权重值的函数即可抑制过大权重

用公式表达即为：
total loss = (1/2)λ * (√∑w²)

其中λ为控制权值衰减的超参数，其值越大权值衰减将越强（可以更好一直过拟合，但也会导致训练难以达到高准确率），加上1/2是为了方便求导

这里L2范数指各权重值的平方和的开方，即√∑w²，与其类似的还有L1范数，指各权重值绝对值的和，L∞（又称Max范数），为权重值中最大值。这三个范数都可用于权值衰减，但一般常用的是L2

再次运行上面测试过拟合的实验程序，但加上权值衰减，λ取值0.1

# coding: utf-8
import os
import sys

sys.path.append("D:\AI learning source code")  # 为了导入父目录的文件而进行的设定
import numpy as np
import matplotlib.pyplot as plt
from dataset.mnist import load_mnist
from common.multi_layer_net import MultiLayerNet
from common.optimizer import SGD

(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True)

# 为了再现过拟合，减少学习数据
x_train = x_train[:300]
t_train = t_train[:300]

# weight decay（权值衰减）的设定 =======================
# weight_decay_lambda = 0 # 不使用权值衰减的情况
weight_decay_lambda = 0.1
# ====================================================

network = MultiLayerNet(input_size=784, hidden_size_list=[100, 100, 100, 100, 100, 100], output_size=10,
                        weight_decay_lambda=weight_decay_lambda)
optimizer = SGD(lr=0.01)

max_epochs = 201
train_size = x_train.shape[0]
batch_size = 100

train_loss_list = []
train_acc_list = []
test_acc_list = []

iter_per_epoch = max(train_size / batch_size, 1)
epoch_cnt = 0

for i in range(1000000000):
    batch_mask = np.random.choice(train_size, batch_size)
    x_batch = x_train[batch_mask]
    t_batch = t_train[batch_mask]

    grads = network.gradient(x_batch, t_batch)
    optimizer.update(network.params, grads)

    if i % iter_per_epoch == 0:
        train_acc = network.accuracy(x_train, t_train)
        test_acc = network.accuracy(x_test, t_test)
        train_acc_list.append(train_acc)
        test_acc_list.append(test_acc)

        print("epoch:" + str(epoch_cnt) + ", train acc:" + str(train_acc) + ", test acc:" + str(test_acc))

        epoch_cnt += 1
        if epoch_cnt >= max_epochs:
            break


# 3.绘制图形==========
markers = {'train': 'o', 'test': 's'}
x = np.arange(max_epochs)
plt.plot(x, train_acc_list, marker='o', label='train', markevery=10)
plt.plot(x, test_acc_list, marker='s', label='test', markevery=10)
plt.xlabel("epochs")
plt.ylabel("accuracy")
plt.ylim(0, 1.0)
plt.legend(loc='lower right')
plt.show()