Q-Learning:Off-Policy TD Control

强化学习的早期突破之一是开发了一种称为Q学习的非策略TD控制算法（Watkins，1989）。其最简单的形式，定义为

$\text{[math]}$ (6.8)

在这种情况下，学习的动作-值函数Q直接近似于最优动作-值函数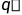 $\text{[math]}$ ，与所遵循的策略无关。这极大地简化了算法的分析，并实现了早期收敛证明。该策略仍然具有影响，因为它确定访问和更新哪些状态-操作对。但是，正确收敛所需要的只是所有对继续更新。正如我们在第5章中所观察到的，这是一个最低要求，因为任何保证在一般情况下找到最佳行为的方法都必须这样要求。在此假设和步长参数序列的通常随机逼近条件的变体下，Qt已被证明以概率 1 收敛到 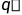$\text{[math]}$ 。Q 学习算法以如下程序形式所示。

Q-learning (off-policy TD control) for estimating $\text{[math]}$

Algorithm parameters: step size $\text{[math]}$ , small $\text{[math]}$

Initialize Q(s,a), for all 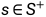$\text{[math]}$ , $\text{[math]}$ arbitrarily except that Q(terminal,.)=0

Loop for each episode:

Initialize S

Loop for each step of episode:

Choose A from S using policy derived from Q (e.g.,ε-greedy)

Take action A, observe R,S'

$\text{[math]}$

S <- S';

until s is terminal

Q-learning的备份图是什么？规则（6.8）更新状态-操作对，因此顶部节点（更新的根节点）必须是小型的填充操作节点。更新也来自操作节点，最大化下一个状态下可能的所有操作。因此，备份关系图的底部节点应该是所有这些操作节点。最后，请记住，我们指示在这些“下一步操作”节点中，它们有一个弧形（图 3.4-右）。您现在能猜出图表是什么吗？如果是这样，请在转到第 134 页图 6.4 中的答案之前进行猜测。