算法分析
研究算法的最终目的就是如何花更少的时间，如何占用更少的内存去完成相同的需求，并且也通过案例演示了不同算法之间时间耗费和空间耗费上的差异，但我们并不能将时间占用和空间占用量化，因此，接下来我们要学习有关算法时间耗费和算法空间耗费的描述和分析。有关算法时间耗费分析，我们称之为算法的时间复杂度分析，有关算法的空间耗费分析，我们称之为算法的空间复杂度分析。
算法的时间复杂度分析
我们要计算算法时间耗费情况，首先我们得度量算法的执行时间，那么如何度量呢？
事后分析估算方法：
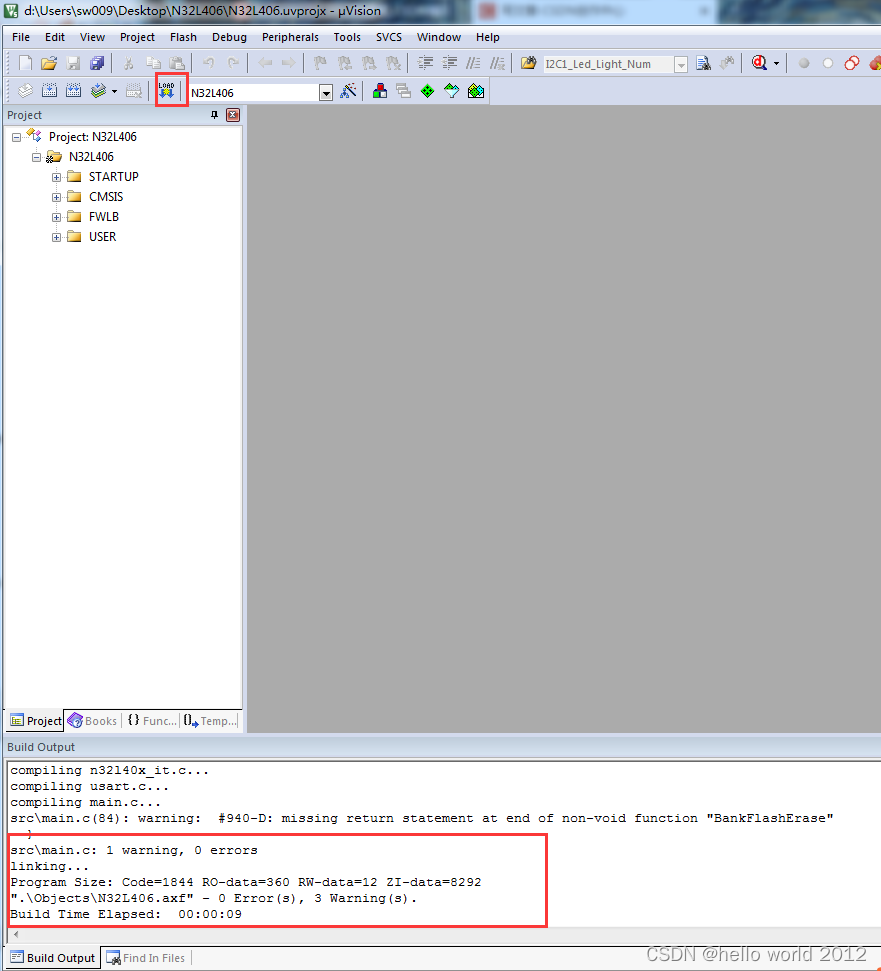
比较容易想到的方法就是我们把算法执行若干次，然后拿个计时器在旁边计时，这种事后统计的方法看上去的确不错，并且也并非要我们真的拿个计算器在旁边计算，因为计算机都提供了计时的功能。这种统计方法主要是通过设计好的测试程序和测试数据，利用计算机计时器对不同的算法编制的程序的运行时间进行比较，从而确定算法效率的高低，但是这种方法有很大的缺陷：必须依据算法实现编制好的测试程序，通常要花费大量时间和精力，测试完了如果发现测试的是非常糟糕的算法，那么之前所做的事情就全部白费了，并且不同的测试环境(硬件环境)的差别导致测试的结果差异也很大。
public static void main(String[] args) {
long start = System.currentTimeMillis();
int sum = 0;
int n=100;
for (int i = 1; i <= n; i++) {
sum += i;
}
System.out.println("sum=" + sum);
long end = System.currentTimeMillis();
System.out.println(end-start);
}事前分析估算方法：
在计算机程序编写前，依据统计方法对算法进行估算，经过总结，我们发现一个高级语言编写的程序程序在计算机
上运行所消耗的时间取决于下列因素：
1.算法采用的策略和方案；
2.编译产生的代码质量；
3.问题的输入规模(所谓的问题输入规模就是输入量的多少)；
4.机器执行指令的速度；
由此可见，抛开这些与计算机硬件、软件有关的因素，一个程序的运行时间依赖于算法的好坏和问题的输入规模。
如果算法固定，那么该算法的执行时间就只和问题的输入规模有关系了。
我么再次以之前的求和案例为例，进行分析。
需求：
计算1到100的和。
第一种解法：
如果输入量为n为1，则需要计算1次；
如果输入量n为1亿，则需要计算1亿次；
public static void main(String[] args) {
int sum = 0;//执行1次
int n=100;//执行1次
for (int i = 1; i <= n; i++) {//执行了n+1次
sum += i;//执行了n次
}
System.out.println("sum=" + sum);
}第二种解法：
如果输入量为n为1，则需要计算1次；
如果输入量n为1亿，则需要计算1次；
public static void main(String[] args) {
int sum = 0;//执行1次
int n=100;//执行1次
sum = (n+1)*n/2;//执行1次
System.out.println("sum="+sum);
}因此，当输入规模为n时，第一种算法执行了1+1+(n+1)+n=2n+3次；第二种算法执行了1+1+1=3次。如果我们把
第一种算法的循环体看做是一个整体，忽略结束条件的判断，那么其实这两个算法运行时间的差距就是n和1的差
距。
为什么循环判断在算法1里执行了n+1次，看起来是个不小的数量，但是却可以忽略呢？我们来看下一个例子：
需求：
计算100个1+100个2+100个3+...100个100的结果
代码：
public static void main(String[] args) {
int sum=0;
int n=100;
for (int i = 1; i <=n ; i++) {
for (int j = 1; j <=n ; j++) {
sum+=i;
}
}
System.out.println("sum="+sum);
}上面这个例子中，如果我们要精确的研究循环的条件执行了多少次，是一件很麻烦的事情，并且，由于真正计算和的代码是内循环的循环体，所以，在研究算法的效率时，我们只考虑核心代码的执行次数，这样可以简化分析。
我们研究算法复杂度，侧重的是当输入规模不断增大时，算法的增长量的一个抽象(规律)，而不是精确地定位需要执行多少次，因为如果是这样的话，我们又得考虑回编译期优化等问题，容易主次跌倒。我们不关心编写程序所用的语言是什么，也不关心这些程序将跑在什么样的计算机上，我们只关心它所实现的算法。这样，不计那些循环索引的递增和循环终止的条件、变量声明、打印结果等操作，最终在分析程序的运行时间时，最重要的是把程序看做是独立于程序设计语言的算法或一系列步骤。我们分析一个算法的运行时间，最重要的就是把核心操作的次数和输入规模关联起来。
函数渐近增长
给定两个函数f(n)和g(n),如果存在一个整数N，使得对于所有的n>N,f(n)总是比g(n)大，那么我们说f(n)的增长渐近快于g(n)。
概念似乎有点艰涩难懂，那接下来我们做几个测试。
测试一：
假设四个算法的输入规模都是n：
1.算法A1要做2n+3次操作，可以这么理解：先执行n次循环，执行完毕后，再有一个n次循环，最后有3次运算；
2.算法A2要做2n次操作；
3.算法B1要做3n+1次操作，可以这个理解：先执行n次循环，再执行一个n次循环，再执行一个n次循环，最后有1
次运算。
4.算法B2要做3n次操作；
那么，上述算法，哪一个更快一些呢？
通过数据表格，比较算法A1和算法B1：
当输入规模n=1时，A1需要执行5次，B1需要执行4次，所以A1的效率比B1的效率低；
当输入规模n=2时，A1需要执行7次，B1需要执行7次，所以A1的效率和B1的效率一样；
当输入规模n>2时，A1需要的执行次数一直比B1需要执行的次数少，所以A1的效率比B1的效率高；
所以我们可以得出结论：
当输入规模n>2时，算法A1的渐近增长小于算法B1 的渐近增长
通过观察折线图，我们发现，随着输入规模的增大，算法A1和算法A2逐渐重叠到一块，算法B1和算法B2逐渐重叠
到一块，所以我们得出结论：
随着输入规模的增大，算法的常数操作可以忽略不计
测试二：
假设四个算法的输入规模都是n：
1.算法C1需要做4n+8次操作
2.算法C2需要做n次操作
3.算法D1需要做2n^2次操作
4.算法D2需要做n^2次操作
那么上述算法，哪个更快一些？
通过数据表格，对比算法C1和算法D1：
当输入规模n<=3时，算法C1执行次数多于算法D1，因此算法C1效率低一些；
当输入规模n>3时，算法C1执行次数少于算法D1，因此，算法D2效率低一些，
所以，总体上，算法C1要优于算法D1.
通过折线图，对比对比算法C1和C2：
随着输入规模的增大，算法C1和算法C2几乎重叠
通过折线图，对比算法C系列和算法D系列：
随着输入规模的增大，即使去除n^2前面的常数因子，D系列的次数要远远高于C系列。
因此，可以得出结论：
随着输入规模的增大，与最高次项相乘的常数可以忽略
测试三：
假设四个算法的输入规模都是n：
算法E1:
2n^2+3n+1;
算法E2：
n^2
算法F1：
2n^3+3n+1
算法F2：
n^3
那么上述算法，哪个更快一些？
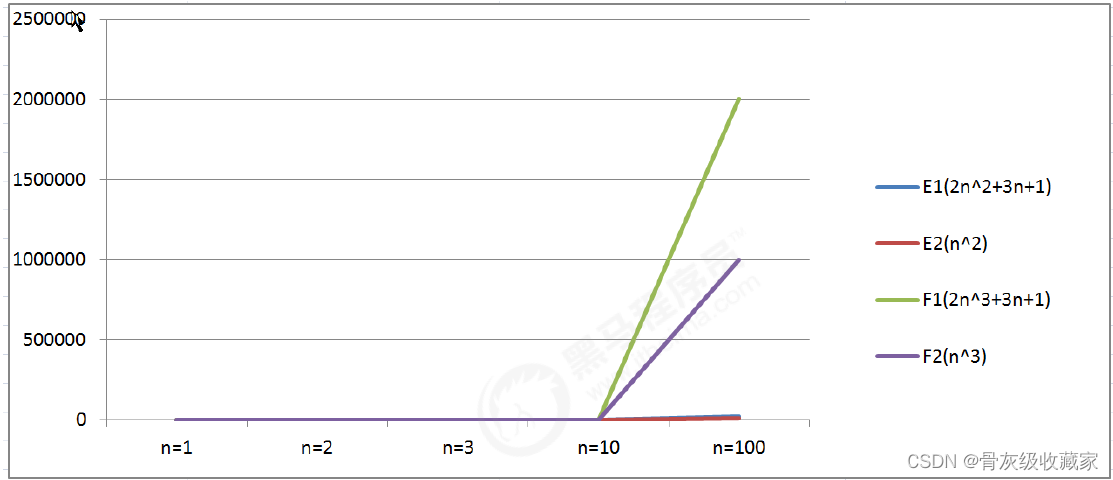通过数据表格，对比算法E1和算法F1：
当n=1时，算法E1和算法F1的执行次数一样；
当n>1时，算法E1的执行次数远远小于算法F1的执行次数；
所以算法E1总体上是由于算法F1的。
通过折线图我们会看到，算法F系列随着n的增长会变得特块，算法E系列随着n的增长相比较算法F来说，变得比较慢，所以可以得出结论：
最高次项的指数大的，随着n的增长，结果也会变得增长特别快
算法时间复杂度
大O记法
定义：
在进行算法分析时，语句总的执行次数T(n)是关于问题规模n的函数，进而分析T(n)随着n的变化情况并确定T(n)的量级。算法的时间复杂度，就是算法的时间量度，记作:T(n)=O(f(n))。它表示随着问题规模n的增大，算法执行时间的增长率和f(n)的增长率相同，称作算法的渐近时间复杂度，简称时间复杂度，其中f(n)是问题规模n的某个函数。
在这里，我们需要明确一个事情：执行次数=执行时间
用大写O()来体现算法时间复杂度的记法，我们称之为大O记法。一般情况下，随着输入规模n的增大，T(n)增长最
慢的算法为最优算法。
下面我们使用大O表示法来表示一些求和算法的时间复杂度：
算法一：
public static void main(String[] args) {
int sum = 0;//执行1次
int n=100;//执行1次
sum = (n+1)*n/2;//执行1次
System.out.println("sum="+sum);
}算法二：
public static void main(String[] args) {
int sum = 0;//执行1次
int n=100;//执行1次
for (int i = 1; i <= n; i++) {
sum += i;//执行了n次
}
System.out.println("sum=" + sum);
}public static void main(String[] args) {
int sum=0;//执行1次
int n=100;//执行1次
for (int i = 1; i <=n ; i++) {
for (int j = 1; j <=n ; j++) {
sum+=i;//执行n^2次
}
}
System.out.println("sum="+sum);
}如果忽略判断条件的执行次数和输出语句的执行次数，那么当输入规模为n时，以上算法执行的次数分别为：
算法一：3次
算法二：n+3次
算法三：n^2+2次
如果用大O记法表示上述每个算法的时间复杂度，应该如何表示呢？基于我们对函数渐近增长的分析，推导大O阶
的表示法有以下几个规则可以使用：
1.用常数1取代运行时间中的所有加法常数；
2.在修改后的运行次数中，只保留高阶项；
3.如果最高阶项存在，且常数因子不为1，则去除与这个项相乘的常数；
所以，上述算法的大O记法分别为：
算法一：O(1)
算法二：O(n)
算法的空间复杂度分析
计算机的软硬件都经历了一个比较漫长的演变史，作为为运算提供环境的内存，更是如此，从早些时候的512k,经
历了1M，2M，4M...等，发展到现在的8G，甚至16G和32G，所以早期，算法在运行过程中对内存的占用情况也是
一个经常需要考虑的问题。我么可以用算法的空间复杂度来描述算法对内存的占用。
java中常见内存占用
1.基本数据类型内存占用情况：
计算机访问内存的方式都是一次一个字节
一个引用（机器地址）需要8个字节表示：
例如： Date date = new Date(),则date这个变量需要占用8个字节来表示
4.创建一个对象，比如new Date()，除了Date对象内部存储的数据(例如年月日等信息)占用的内存，该对象本身也有内存开销，每个对象的自身开销是16个字节，用来保存对象的头信息。
5.一般内存的使用，如果不够8个字节，都会被自动填充为8字节：
6.java中数组被被限定为对象，他们一般都会因为记录长度而需要额外的内存，一个原始数据类型的数组一般需要24字节的头信息(16个自己的对象开销，4字节用于保存长度以及4个填充字节)再加上保存值所需的内存。
算法的空间复杂度
了解了java的内存最基本的机制，就能够有效帮助我们估计大量程序的内存使用情况。
算法的空间复杂度计算公式记作：S(n)=O(f(n)),其中n为输入规模，f(n)为语句关于n所占存储空间的函数。
案例：
对指定的数组元素进行反转，并返回反转的内容。
解法一：
public static int[] reverse1(int[] arr){
int n=arr.length;//申请4个字节
int temp;//申请4个字节
for(int start=0,end=n-1;start<=end;start++,end--){
temp=arr[start];
arr[start]=arr[end];
arr[end]=temp;
}
return arr;
}解法二：
public static int[] reverse2(int[] arr){
int n=arr.length;//申请4个字节
int[] temp=new int[n];//申请n*4个字节+数组自身头信息开销24个字节
for (int i = n-1; i >=0; i--) {
temp[n-1-i]=arr[i];
}
return temp;
}忽略判断条件占用的内存，我们得出的内存占用情况如下：
算法一：
不管传入的数组大小为多少，始终额外申请4+4=8个字节；
算法二：
4+4n+24=4n+28;
根据大O推导法则，算法一的空间复杂度为O(1),算法二的空间复杂度为O(n),所以从空间占用的角度讲，算法一要
优于算法二。
由于java中有内存垃圾回收机制，并且jvm对程序的内存占用也有优化（例如即时编译），我们无法精确的评估一个java程序的内存占用情况，但是了解了java的基本内存占用，使我们可以对java程序的内存占用情况进行估算。
由于现在的计算机设备内存一般都比较大，基本上个人计算机都是4G起步，大的可以达到32G，所以内存占用一般情况下并不是我们算法的瓶颈，普通情况下直接说复杂度，默认为算法的时间复杂度。但是，如果你做的程序是嵌入式开发，尤其是一些传感器设备上的内置程序，由于这些设备的内存很小，一般为几kb，这个时候对算法的空间复杂度就有要求了，但是一般做java开发的，基本上都是服务器开发，一般不存在这样的问题。
