💌 所属专栏:【LeetCode题解(持续更新中)】
😀 作 者:我是夜阑的狗🐶
🚀 个人简介:一个正在努力学技术的CV工程师,专注基础和实战分享 ,欢迎咨询!
💖 欢迎大家:这里是CSDN,我总结知识的地方,喜欢的话请三连,有问题请私信 😘 😘 😘
您的点赞、关注、收藏、评论,是对我最大的激励和支持!!!🤩 🤩 🤩
文章目录
- 前言
- 一、编程题:面试题 01.07. 旋转矩阵(原地旋转+翻转替旋转)
- 1.题目描述
- 2.示例1:
- 3.示例2:
- 二、解题思路
- 1. 方法1(原地旋转)
- 思路:
- 复杂度分析:
- 算法图解
- 2. 方法二:翻转替旋转
- 思路:
- 复杂度分析:
- 算法图解
- 三、代码实现
- 总结
前言
大家好,又见面了,我是夜阑的狗✨,本文是专栏【LeetCode题解】专栏的第21篇文章,主要讲解的是LeetCode 面试题 01.07. 旋转矩阵(原地旋转+翻转替旋转)。
专栏地址:【LeetCode题解(持续更新中)】, 此专栏是我是夜阑的狗对LeetCode问题的讲解,希望能够加深自己的印象,以及帮助到其他的小伙伴😉😉。
如果文章有什么需要改进的地方还请大佬不吝赐教👏👏。
一、编程题:面试题 01.07. 旋转矩阵(原地旋转+翻转替旋转)
1.题目描述
给你一幅由 N × N 矩阵表示的图像,其中每个像素的大小为 4 字节。请你设计一种算法,将图像旋转 90 度。
不占用额外内存空间能否做到?LeetCode题目链接。
2.示例1:
给定 matrix =
[
[1,2,3],
[4,5,6],
[7,8,9]
],
原地旋转输入矩阵,使其变为:
[
[7,4,1],
[8,5,2],
[9,6,3]
]
3.示例2:
给定 matrix =
[
[ 5, 1, 9,11],
[ 2, 4, 8,10],
[13, 3, 6, 7],
[15,14,12,16]
],
原地旋转输入矩阵,使其变为:
[
[15,13, 2, 5],
[14, 3, 4, 1],
[12, 6, 8, 9],
[16, 7,10,11]
]
注意:本题与主站 48 题相同:https://leetcode-cn.com/problems/rotate-image/
二、解题思路
1. 方法1(原地旋转)
为了不使用额外内存空间,可以采用数学公式推导出原地旋转的方法;
矩阵旋转90度,对比旋转前后元素的位置,可以得到这么一个规律:
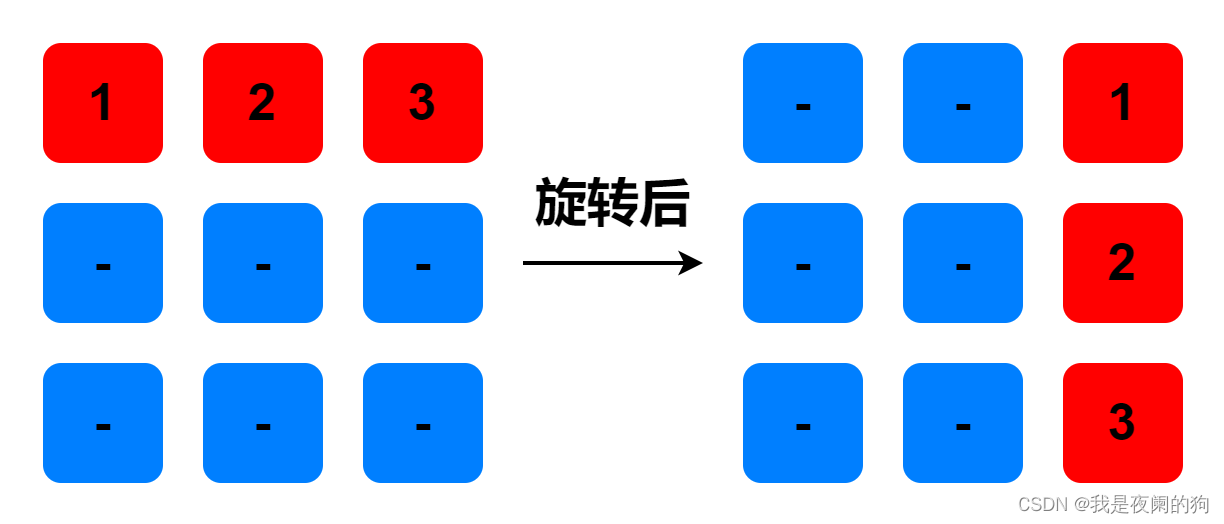
矩阵中第
i行的第j个元素,旋转后出现在第n-i列的第j个位置;(n为矩阵的行列数)
根据这个规律可以得到:matrix[j][n-i-1] = matrix[i][j](1)。这里因为矩阵中行列从0开始计数,所以旋转后列位置要减1;
接下来要根据公式(1)推导出下面三个位置:

首先我们可以知道2的位置为a[i][j],将其代入公式(1)得到6的位置a[j][n-i-1],同理可以再把6的位置代入公式(1)得到8的位置a[n-i-1][n-j-1],在重复一次最后得到4的位置a[n-j-1][i]。
这里知道这4个位置之后,这四个位置变量进行交换则需要一个额外变量temp来进行操作:
{ t e m p = a [ i ] [ j ] a [ i ] [ j ] = a [ n − j − 1 ] [ i ] a [ n − j − 1 ] [ i ] = a [ n − i − 1 ] [ n − j − 1 ] a [ n − j − 1 ] [ n − i − 1 ] = a [ j ] [ n − i − 1 ] a [ j ] [ n − i − 1 ] = t e m p ( 2 ) \begin{cases} temp\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ = a[i][j] \\ a[i][j] \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ = a[n-j-1][i] \\ a[n-j-1][i] \ \ \ \ \ \ \ \ \ \ \ \ \ \ = a[n-i-1][n-j-1] \\ a[n-j-1][n-i-1] = a[j][n-i-1] \\ a[j][n-i-1] \ \ \ \ \ \ \ \ \ \ \ \ \ \ = temp \end{cases} (2) ⎩ ⎨ ⎧temp =a[i][j]a[i][j] =a[n−j−1][i]a[n−j−1][i] =a[n−i−1][n−j−1]a[n−j−1][n−i−1]=a[j][n−i−1]a[j][n−i−1] =temp(2)
思路:
- Step 1.由上面的推导过程可以知道用公式(2)对矩阵进行原地旋转;
- Step 2.矩阵为偶数时,需要遍历
(n/2)x(n/2)(3)个位置,矩阵为奇数时,需要遍历(n-1)/2x(n+1)/2(4)个位置,根据(3)(4)可以知道要满足这两个要求需要遍历n/2x(n+1)/2(5)个位置; - Step 3.根据公式(2)(5)就完整实现矩阵原地旋转;
看不懂解释的话,直接看算法图解比较容易理解点
复杂度分析:
时间复杂度:O(N^2),其中N是矩阵的边长,最大遍历个数为O([n/2]x[(n+1)/2]) = O(N^2)。
空间复杂度:O(1)。原地旋转。
算法图解
- 当n为偶数时,最少需要遍历
(n/2)x(n/2)(3)个位置,红色部分表示遍历的位置;(注:本人不会做成流程动画,希望会的朋友可以私信我指点一二,说个软件名字也可以,谢谢 🤩 🤩 🤩)

- 当n为奇数时,由于中心的位置经过旋转后位置不变,最少需要遍历
(n-1)/2x(n+1)/2(4)个位置,红色部分表示遍历的位置;

2. 方法二:翻转替旋转
当然也可以用翻转操作来实现旋转操作(大学高等代数里就有讲过这个基础内容),这里翻转顺序是可以不唯一的,可以先水平翻转在对角线翻转,或者对角线翻转在水平翻转,垂直翻转跟对角线翻转也可以,关键是要看对角线翻转的方向,下面以水平翻转+对角线翻转为例;
思路:
- Step 1.首先进行水平翻转,根据算法图解可以知道位置转换
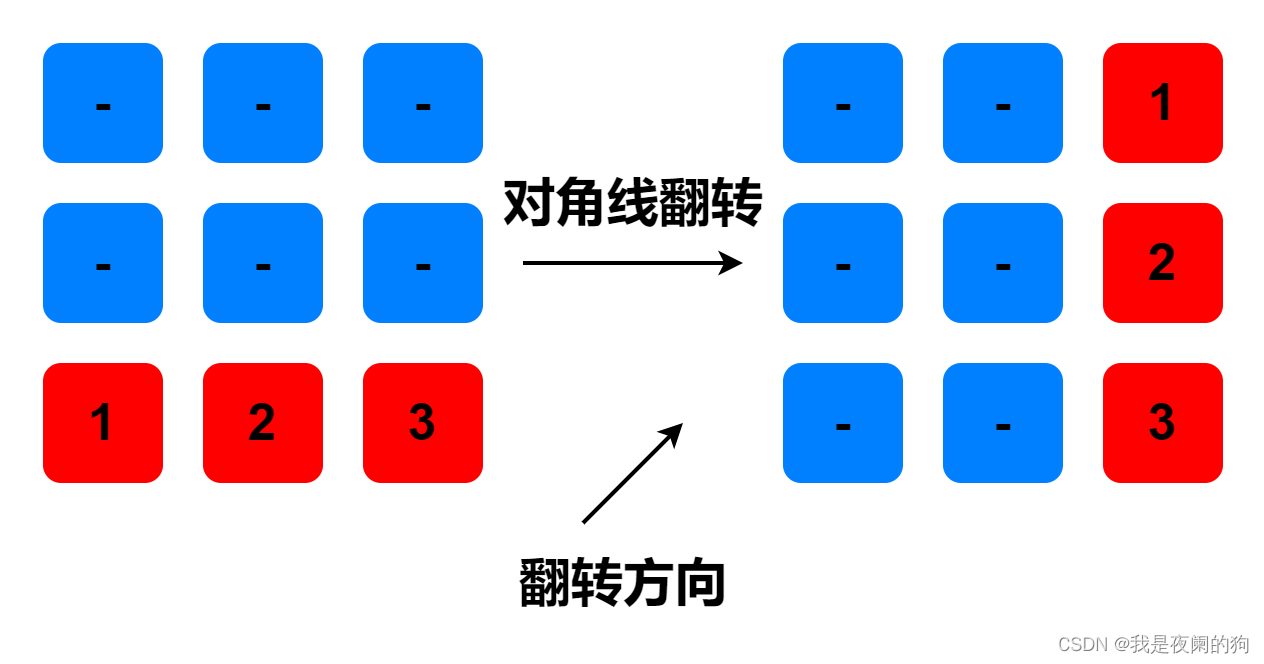
a[i][j] = a[n - i - 1][j](6); - Step 2.接着对角线翻转,根据算法图解可以知道位置转换
a[i][j] = a[j][i](7)。这里最重要的翻转的方向; - Step 3.根据公式(6)(7)就完整实现矩阵翻转替原地旋转;
看不懂解释的话,直接看算法图解比较容易理解点
复杂度分析:
时间复杂度:O(N^2),其中N是矩阵的边长,对于每一次翻转操作,我们都需要枚举矩阵中一半的元素。
空间复杂度:O(1)。原地旋转。
算法图解
水平翻转;(注:本人不会做成流程动画,希望会的朋友可以私信我指点一二,说个软件名字也可以,谢谢)
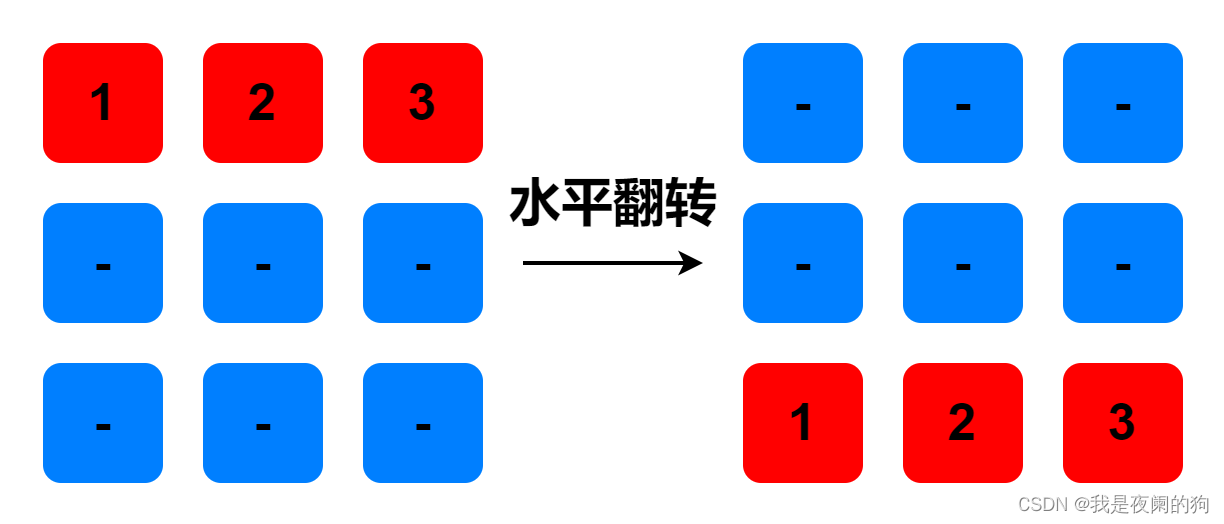
对角线翻转(重点是方向,别翻转错了!!!😂 😂 😂);
三、代码实现
每个代码块都写了注释,方便理解,代码还可以改进;
方法一:原地旋转
class Solution {
public void rotate(int[][] matrix) {
// 旋转对称
int n = matrix.length, temp;
for(int i = 0; i < n/2; i++){
for(int j = 0; j < (n+1)/2; j++){
temp = matrix[i][j];
matrix[i][j] = matrix[n - 1 - j][i];
matrix[n - 1 - j][i] = matrix[n - 1 - i][n - 1 - j];
matrix[n - 1 -i][n - 1 - j] = matrix[j][n - 1 - i];
matrix[j][n - 1 - i] = temp;
}
}
}
}
提交结果:

方法二:翻转替旋转
class Solution {
public void rotate(int[][] matrix) {
// 旋转对称
int n = matrix.length, temp;
//水平翻转
for(int i = 0; i < n/2; i++){
for(int j = 0; j < n; j++){
temp = matrix[i][j];
matrix[i][j] = matrix[n - 1 - i][j];
matrix[n - 1 - i][j] = temp;
}
}
//对角线
for(int i = 0; i < n; i++){
for(int j = 0; j < i; j++){
temp = matrix[i][j];
matrix[i][j] = matrix[j][i];
matrix[j][i] = temp;
}
}
}
}
}
提交结果:
总结
感谢观看,如果有帮助到你,请给题解点个赞和收藏,让更多的人看到。🌹 🌹 🌹
也欢迎你,关注我。👍 👍 👍
原创不易,还希望各位大佬支持一下,你们的点赞、收藏和留言对我真的很重要!!!💕 💕 💕 最后,本文仍有许多不足之处,欢迎各位认真读完文章的小伙伴们随时私信交流、批评指正!
更多专栏订阅:
- 😀 【LeetCode题解(持续更新中)】
- 🚝 【Java Web项目构建过程】
- 💛 【数字图像处理】
- ⚽ 【JavaScript随手笔记】
- 🤩 【大数据学习笔记(华为云)】
- 🦄 【程序错误解决方法(建议收藏)】
- 🚀 【软件安装教程】
订阅更多,你们将会看到更多的优质内容!!

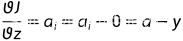
![buu [UTCTF2020]basic-crypto 1](https://img-blog.csdnimg.cn/6011adb31fbd4c42ada2ccc3f5e37ae8.png)