有 N件物品和一个容量是 V的背包。每件物品只能使用一次。

第 i件物品的体积是 vi，价值是 wi。

求解将哪些物品装入背包，可使这些物品的总体积不超过背包容量，且总价值最大。
输出最大价值。

输入格式 

第一行两个整数，N，V用空格隔开，分别表示物品数量和背包容积。

接下来有 N行，每行两个整数 vi,wi，用空格隔开，分别表示第 i 件物品的体积和价值。

输出格式 

输出一个整数，表示最大价值。

数据范围： 

0<N,V≤1000
0<vi,wi≤1000 

输入样例： 

4 5

1 2

2 4

3 4 

4 5 

输出样例： 

8 

注意：本题比较坑的地方就是物品的体积和价值不唯一，可以重复，如果想不到动态规划用暴力解法的话要注意。 

朴素版动态规划如下：

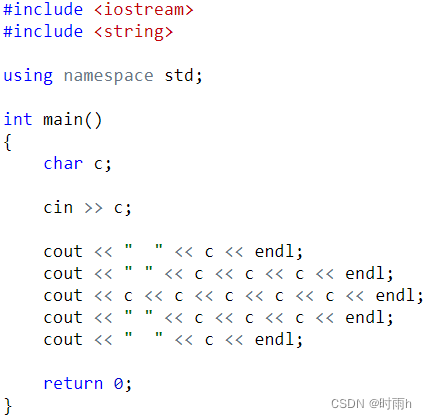
import java.util.*;
 
public class Main {
	public static int N = 1010;
    public static void main(String[] args) {
      Scanner sc = new Scanner(System.in);
      int v[] = new int[N];
      int M[] = new int[N];
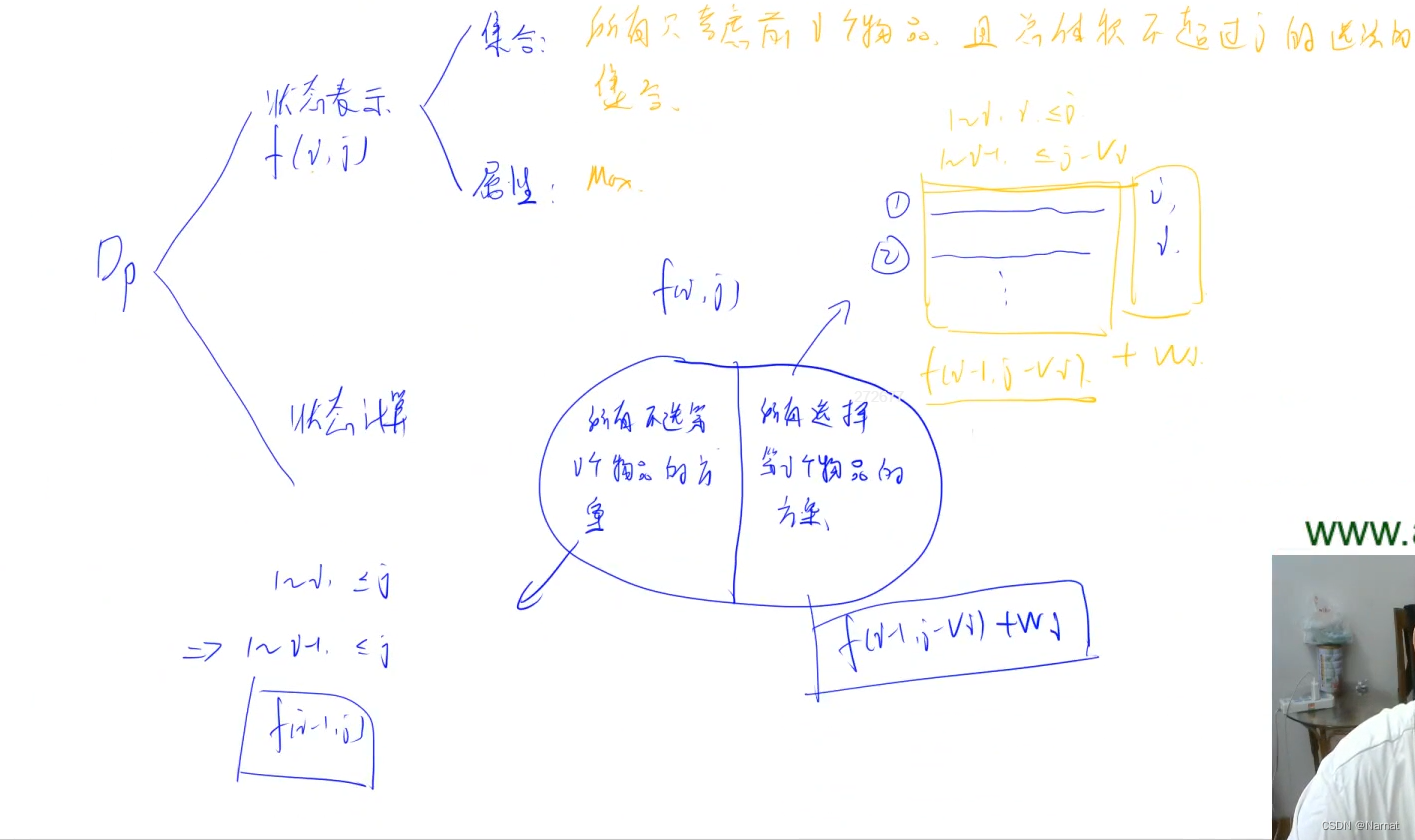
      int f[][] = new int[N][N];//代表函数f(i,j)=price,其意义是考虑前i件物品，且背包体积为j时所能装入的最大价值
      int n = sc.nextInt();
      int m = sc.nextInt();//物品数，体积
      for(int i = 1; i <= n; i ++) {
    	 v[i] = sc.nextInt();
    	 M[i] = sc.nextInt();
      }
      for(int i = 1; i <=n; i++)//i代表考虑前i件物品
    	  for(int j = 0; j <=m; j++) {//j表示背包体积为j时（体积可以为零0，所以由0开始）
    	     f[i][j] = f[i-1][j];//不装入第i件物品
    	     if(j >= v[i]) f[i][j] = Math.max(f[i][j], f[i - 1][j - v[i]] + M[i]);//装入第i件物品
    	  }//由初始往上递推，储存了必要值。
      System.out.print(f[n][m]);
	  }
}

 实在没事思路可以在：对应01背包问题后方找这位大哥的视频讲解

精华版（不好理解，由上述代码优化而来，思路完全一样）：

import java.util.*;
 
public class Main {
	public static int N = 1010;
    public static void main(String[] args) {
      Scanner sc = new Scanner(System.in);
      int v[] = new int[N];
      int M[] = new int[N];
      int f[] = new int[N];
      int n = sc.nextInt();
      int m = sc.nextInt();
      for(int i = 1; i <= n; i ++) {
    	  v[i] = sc.nextInt();
    	  M[i] = sc.nextInt();
      }
      for(int i = 1; i <= n;i++)
    	  for(int j = m; j >= v[i]; j--) f[j] = Math.max(f[j], f[j - v[i]] + M[i]);
      System.out.print(f[m]);
	  }
}

01背包本质上：由简单到易计算并记录每一个状态的最优解，根据记录的最优解推广到下一个状态的最优解，就这样层层递推。

递推：对于第i件物品，无非分为装与不装两个状态，装入就先装第i件物品，再查找剩下背包状态最优解并相加。不装就是取记录的i - 1件物品最优解。两者取最大即新状态最优解。