$e.g.$
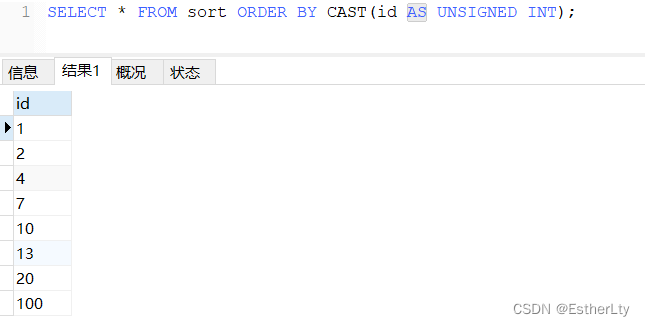
假设你想要卖一个房子，希望可以用人工智能来算出能卖多少钱。机器学习可以根据提供的数据集合构建出很多模型，但是到底哪种模型最好的拟合你的数据？或者说，哪种模型可以最准确的算出你的卖多少钱？

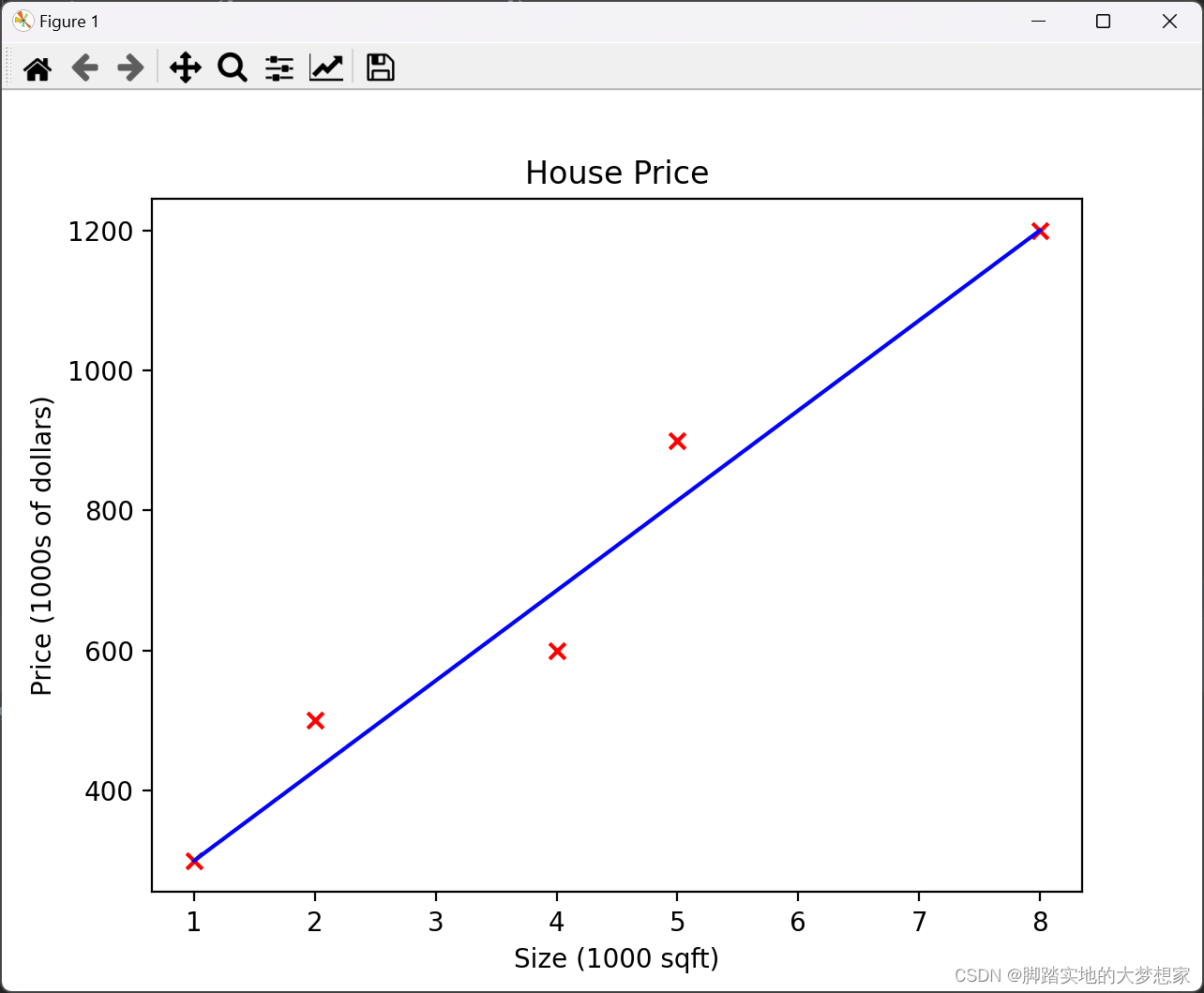
假设机器提出的第一种模型：

假设机器提出的第二种模型：

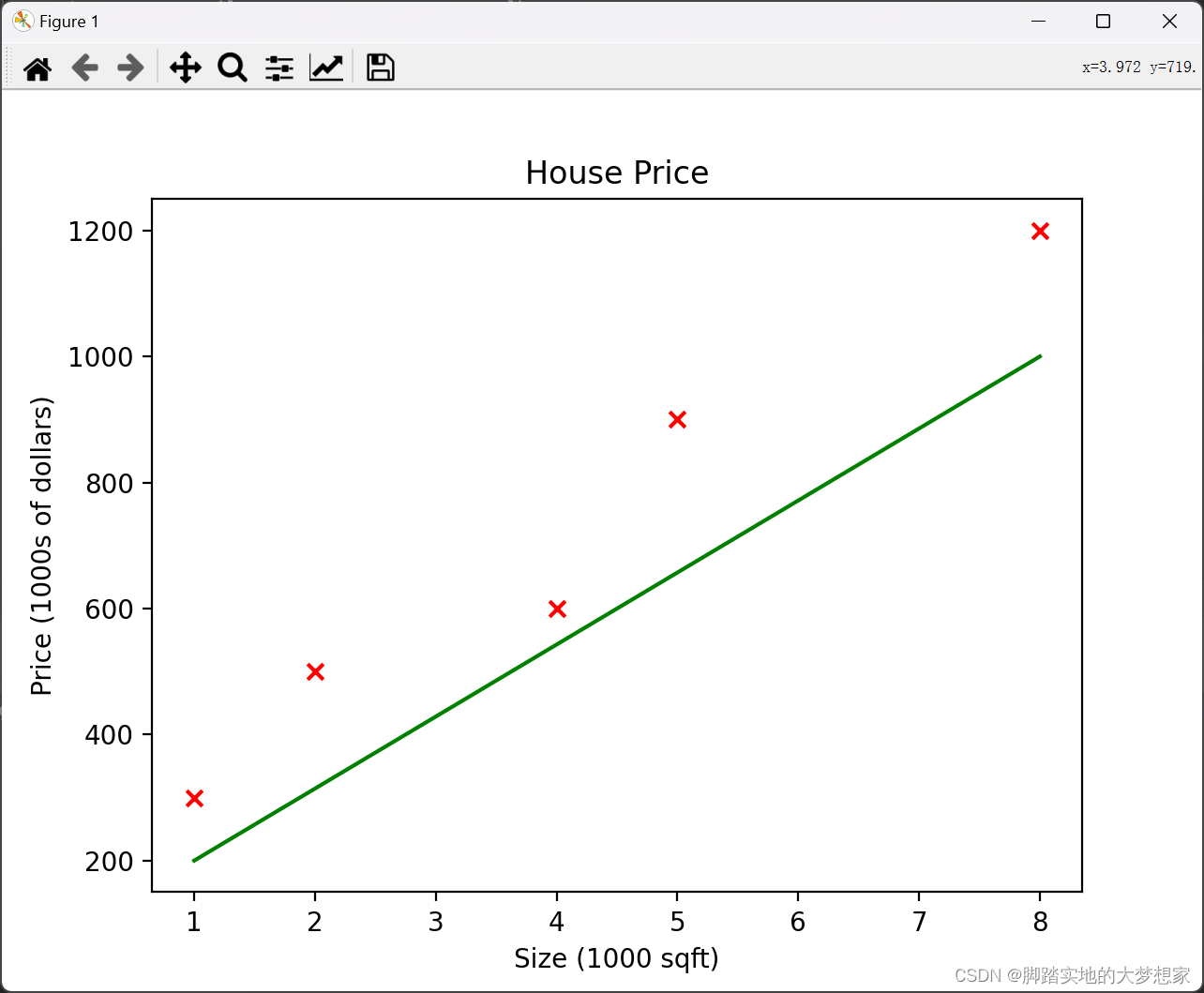
很明显第一种更好的拟合数据结果，但是我们如何用量化去判断？
用 Cost Function，损失函数

$$J(w,b)=\frac{1}{2m}\sum _{i=1}^m(f_{w,b}(x^{(i)})-y^{(i)}{)}^2$$

其中：
$f_{w,b}(x^{(i)})=wx+b$
$y^{(i)}$为实际值，即Label

该函数（损失函数）的含义是通过计算所有点的实际值与预测值的差的平方作为判断哪种模型更好的拟合数据。以此种方法作为量化判断模型的方法。

P.S. 不要纠结于为什么是 $\frac{1}{2m}$ 而不是 $\frac{1}{m}$，这个最好的解释就是，习惯。加不加2不影响其损失函数值大小的判断。

---

但是实际生活中就像如上所述，一般一个结果是由于很多因素共同构成的结果，即：
$y=w_1{x}_1+w_2{x}_2+...+w_n{x}_n+b$

假设函数为： $f(x)=wx+b$

我们用Python程序写出损失函数的计算公式：

$J(w,b)=\frac{1}{2m}{\sum }_{i=1}^m(f_{w,b}(x^{(i)})-y^{(i)}{)}^2$

def compute_cost(x, y, w, b):
	m = x.shape[0]   
    cost_sum = 0
    for i in range(m): 
        f_wb = w * x[i] + b   
        cost = (f_wb - y[i]) ** 2  
        cost_sum = cost_sum + cost  
    total_cost = (1 / (2 * m)) * cost_sum  

    return total_cost