计算机视觉偏底层的工作会跟摄像机打交道,最近正好有接触,所以整理总结一下。
相机参数通常分为内参数、外参数,偶尔会有畸变参数等滤镜参数。
申明:本文图例均为原创,借用需附此文链接。
内参数:相机内部的参数,包括焦距、像素偏移等。
外参数:相机摆放的位置、角度等。
本文主要介绍相机内参数,并且给出简单的数学推理。
必需预备知识:初中数学+初中物理(不满足条件的不用往下看了-_-)
这里用到的物理知识是“光沿直线传播”,用到的数学知识是“相似三角形”。相机成像用到的是“小孔成像原理”,相机内部有一块平面感光元件,物体光线通过光圈(小孔成像的小孔)打到平面感光元件上完成成像。
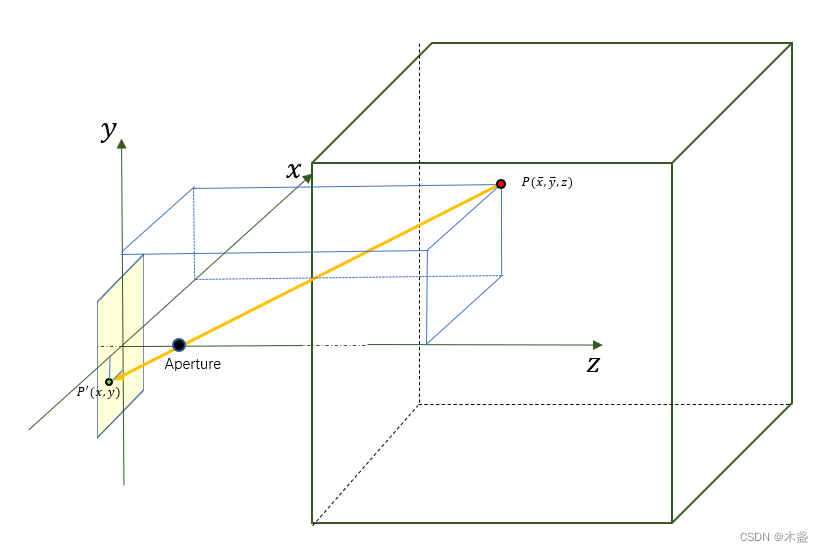
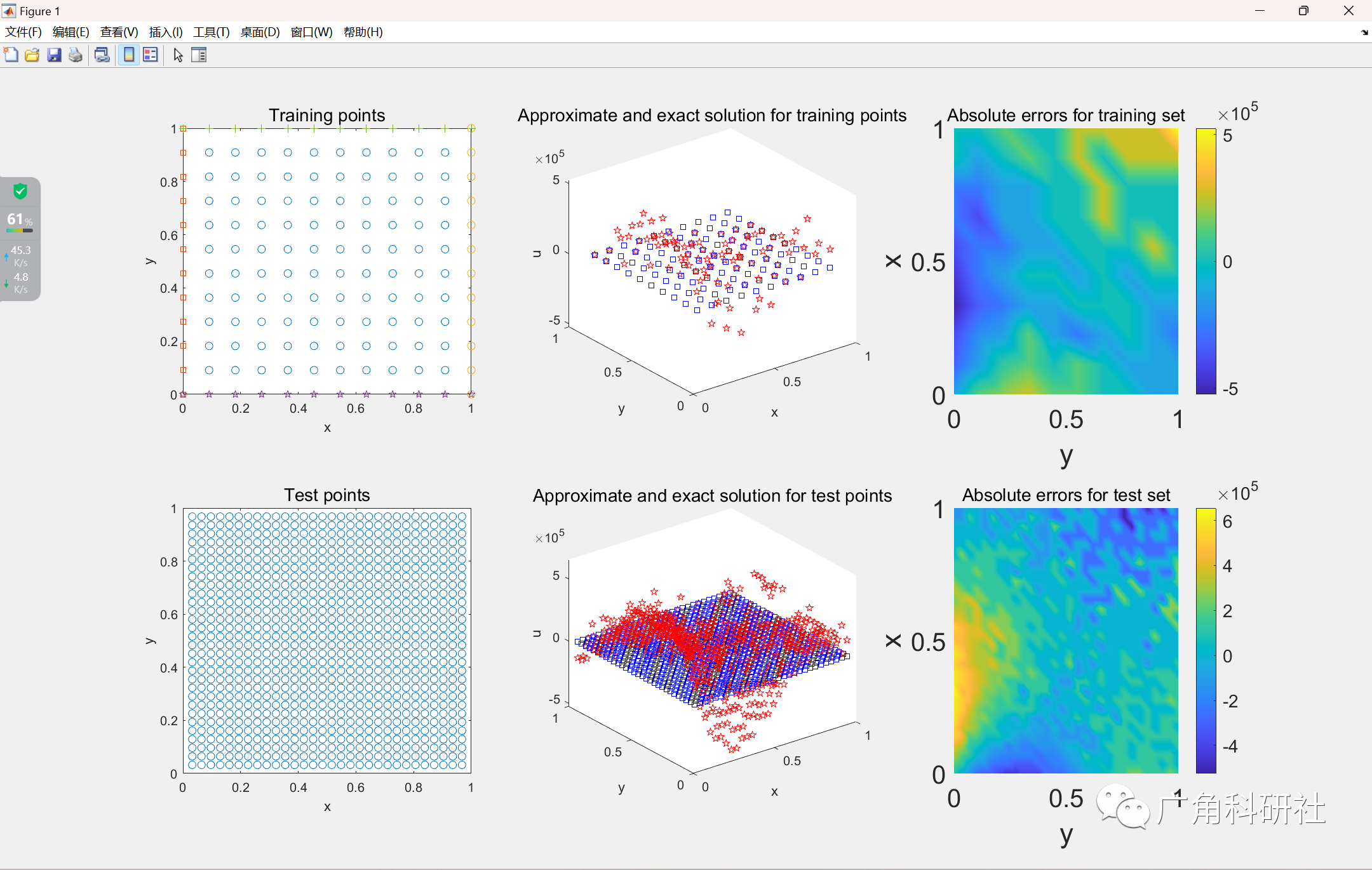
相机成像无非就是把真实世界里三维坐标里的一个点投影到胶片平面上。图1里描述了空间中一个点
P
(
x
ˉ
,
y
ˉ
,
z
)
P(\bar{x},\bar{y},z)
P(xˉ,yˉ,z)投影到平面(图中黄色部分)点
P
′
(
x
,
y
)
P^{'}(x,y)
P′(x,y),在这里为了方便理解,我构建了一个坐标系,原点位置为二维平面的中心位置,z轴方向为相片法向量向外。
重点:相机成像就是做个
(
x
ˉ
,
y
ˉ
,
z
)
(\bar{x},\bar{y},z)
(xˉ,yˉ,z)到
(
x
,
y
)
(x,y)
(x,y)的计算。
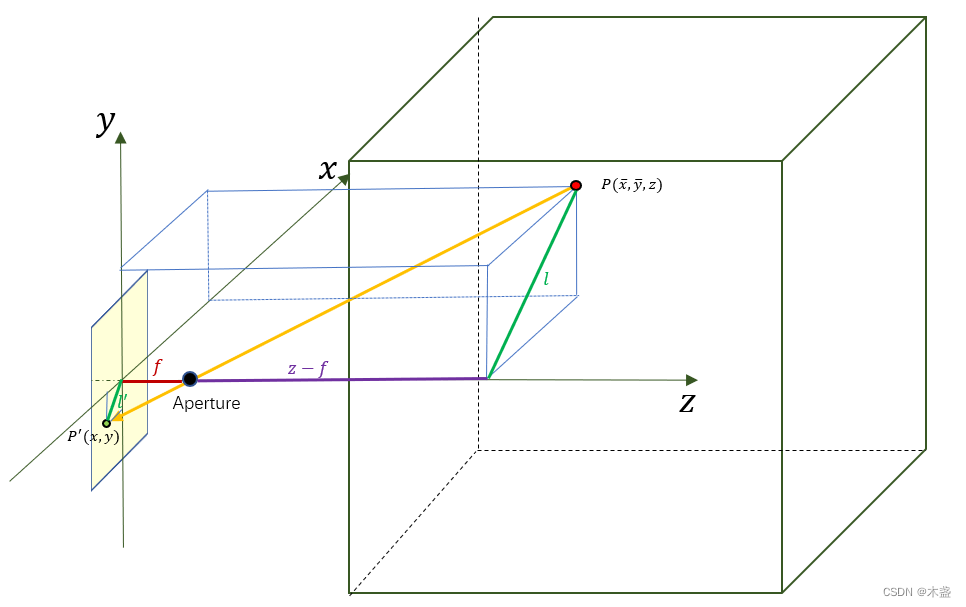
咱们可以构建一个相似三角形,有
f
/
(
z
−
f
)
=
l
′
/
l
=
x
/
x
ˉ
=
y
/
y
ˉ
(1)
f/(z-f)=l^{'}/l=x/\bar{x}=y/\bar{y} \tag{1}
f/(z−f)=l′/l=x/xˉ=y/yˉ(1)
所以,
{
x
=
x
ˉ
f
/
(
z
−
f
)
y
=
y
ˉ
f
/
(
z
−
f
)
(2)
\begin{cases} x=\bar{x}f/(z-f)\\ y=\bar{y}f/(z-f)\\ \end{cases} \tag{2}
{x=xˉf/(z−f)y=yˉf/(z−f)(2)
通常图像坐标原点并不是图像中心点,而是左上角,于是需要加一个偏移量
O
x
O_x
Ox、
O
y
O_y
Oy来对应像素坐标。所以,式子变为
{
x
=
x
ˉ
f
/
(
z
−
f
)
+
O
x
y
=
y
ˉ
f
/
(
z
−
f
)
+
O
y
(3)
\begin{cases} x=\bar{x}f/(z-f)+O_x\\ y=\bar{y}f/(z-f)+O_y\\ \end{cases} \tag{3}
{x=xˉf/(z−f)+Oxy=yˉf/(z−f)+Oy(3)
咱们可以将Aperture(即孔径点)定义成我们坐标系的原点,以换取更简单的表示形式,则图2中紫色部分的
(
z
−
f
)
(z-f)
(z−f)就变成了
z
z
z,替换式子得到
{
x
=
x
ˉ
f
/
z
+
O
x
y
=
y
ˉ
f
/
z
+
O
y
(4)
\begin{cases} x=\bar{x}f/z+O_x\\ y=\bar{y}f/z+O_y\\ \end{cases} \tag{4}
{x=xˉf/z+Oxy=yˉf/z+Oy(4)
改写成齐次矩阵乘积描述形式,
[
x
y
1
]
=
1
z
[
f
0
O
x
0
f
O
y
0
0
1
]
[
x
ˉ
y
ˉ
z
]
(5)
\left[ \begin{matrix} x \\ y \\ 1 \end{matrix} \right] ={1\over{z}} \left[ \begin{matrix} f & 0 & O_x\\ 0 & f & O_y\\ 0 & 0 & 1 \end{matrix} \right] \left[ \begin{matrix} \bar{x} \\ \bar{y} \\ z \end{matrix} \right] \tag{5}
xy1
=z1
f000f0OxOy1
xˉyˉz
(5)
内参数包含焦距
f
f
f、两个方向的中心偏移量
O
x
O_x
Ox、
O
y
O_y
Oy。通常,用矩阵
K
K
K来描述内参数,
K
=
[
f
0
O
x
0
f
O
y
0
0
1
]
(6)
K= \left[ \begin{matrix} f & 0 & O_x\\ 0 & f & O_y\\ 0 & 0 & 1\end{matrix} \right] \tag{6}
K=
f000f0OxOy1
(6)
所以,式(5)可以写成
[
x
y
1
]
=
1
z
K
[
x
ˉ
y
ˉ
z
]
(7)
\left[ \begin{matrix} x \\ y \\ 1 \end{matrix} \right] ={1\over{z}} K \left[ \begin{matrix} \bar{x} \\ \bar{y} \\ z \end{matrix} \right] \tag{7}
xy1
=z1K
xˉyˉz
(7)
通过这个内参数公式,我们可以通过像素(二维)坐标,反算出相机(三维)坐标。
[
x
ˉ
y
ˉ
z
]
=
z
K
−
1
[
x
y
1
]
(8)
\left[ \begin{matrix} \bar{x} \\ \bar{y} \\ z \end{matrix} \right]=zK^{-1}\left[ \begin{matrix} x \\ y \\ 1 \end{matrix} \right] \tag{8}
xˉyˉz
=zK−1
xy1
(8)
根据式(8),若想从像素(二维)坐标拿到相机坐标(三维)坐标,还需要知道深度信息,即目标点离相机的距离。
文毕,有疑问或指导请留言交流!
![[SSD固态硬盘技术 15] FTL映射表的神秘面纱](https://img-blog.csdnimg.cn/img_convert/c1213fdcabb34ef2af8cb706aa6ae2b7.png)