RMQ(Range Minimum/Maximum Query)
- RMQ解决的问题
- ST算法 O(nlogn)
- 线段树
- 例题
- 数列区间最大值
- 最敏捷的机器人
- 天才的记忆
- Frequent values
- 总结(ST和线段树对比)
RMQ解决的问题
RMQ是一个解决多个区间最值查询的算法,即区间最值查询;
如果我们要查询某一个区间内的最值,显然我们可以用暴力搜索的方式在O(n)的时间复杂度内获得结果,但是当我们要查询10000个不同区间内的最值时,我们如果依然采用暴力搜索的方式,那么时间复杂度就会变成O(mn),其中m指的是查询次数,n指的是数据个数。
RMQ算法的目标就是降低多区间最值查询问题的时间复杂度,一般还可以使用线段树求解,复杂度是O(mlogn) 。但还有一种更简便的ST算法,预处理复杂度是O(nlogn),查询O(1)。
RMQ四种解法
ST算法 O(nlogn)
ST(Sparse Table)即稀疏表,算法是通过动态规划思想实现的,他需要在O(nlogn)的时间复杂度内预处理出部分区间的最值,在O(1)的时间内获得一个区间的最值查询结果。总的时间复杂度被降到了O(nlogn)。
预处理 O(nlogn)
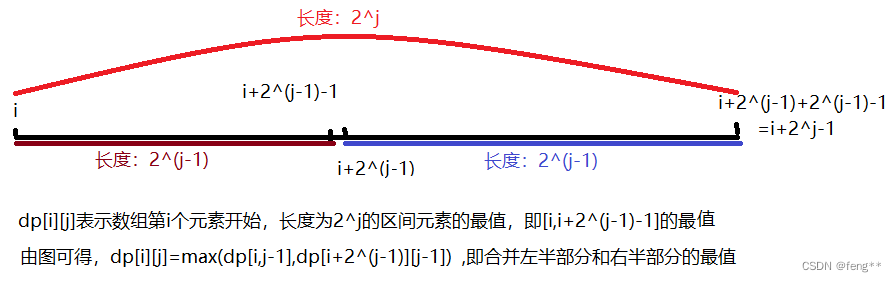
dp[i][j]表示数组第i个元素开始,长度为2^j的区间内的最值。
根据这种dp定义方式,我们可以轻松获得dp[i][j]的递推公式:
dp[i][j]=max(dp[i][j-1],dp[i+2^(j-1)][j-1]);
原理类似倍增,首先比较每2个元素的最值,然后再通过比较这2个最值,得到4个元素的最值,以此类推8个、16个……不断地枚举区间长度,,对每种区间长度求出所有不同起点的区间的最值。
代码实现:
void ST()
{
//下标i最好是从1开始
for(int i=1;i<=n;i++) dp[i][0]=a[i]; //区间长度为1时最值就是自己
//int t=(int)(log(n) / log(2)); j<=t也可以
for(int j=1;pow(2,j)<=n;j++) //枚举区间的长度 ,必须先遍历j再遍历i
{
for(int i=1;i+pow(2,j)-1<=n;i++) //保证左右合并后的区间的r不超过最后下标n
{
dp[i][j]=max(dp[i][j-1],dp[i+pow(2,j-1)][j-1]);
}
}
}
void ST()
{
for(int i=1;i<=n;i++) dp[i][0]=a[i];
for(int j=1;1<<j<=n;j++)
{
for(int i=1;i+1<<j-1<=n;i++) //用左移的方式更快一些
{
dp[i][j]=max(dp[i][j-1],dp[i+(1<<(j-1))][j-1]);
}
}
}
查询 O(1)
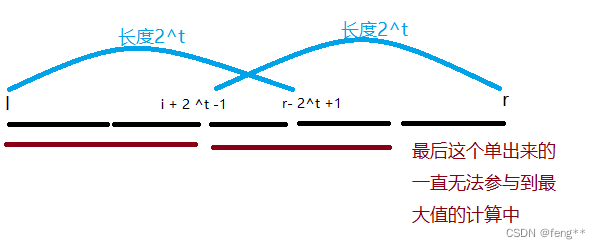
预处理算法的每个区间除了第一个以外都是偶数,那万一他给个不符合条件的区间怎么办,也就是显然我们似乎不能直接一步从dp数组中得到问题的答案,这里我们采用的是从两个有重叠的区间中找到我们需要的答案,这两个重叠的区间一定会包含[l,r]区间内的所有元素
我们需要先算出不超过这个区间长度的 2^ t的t的最大值:log2(r−l+1) 。
那么这个区间的最大值就为 “从l开始的2^ t 个数” 和 “以r结尾的2^ t个数” 这两段的最大值较大的一个。即 max(f[l][t], f[r-(1<<t)+1][t])。
2^t是不超过区间长度r-l+1的最大的数,那2 ^(t+1)一定是超过r-l+1的,也就是前2 ^t个数和后2 ^t个数的和2 ^(t+1)个数的长度一定是大于等于区间长度r-l+1的,因此前后区间能够囊括这个区间内的所有数
代码实现:
//查询
LL query(LL l,LL r)
{
LL t=log2(r-l+1);
return max(dp[l][t],dp[r-(1<<t)+1][t]);
}
线段树
线段树是一种二叉搜索树,与区间树相似,它将一个区间划分成一些单元区间,每个单元区间对应线段树中的一个叶结点。对于线段树中的每一个非叶子节点[a,b],它的左儿子表示的区间为[a,(a+b)/2],右儿子表示的区间为[(a+b)/2+1,b]。因此线段树是平衡二叉树,最后的子节点数目为N,即整个线段区间的长度。使用线段树可以快速的查找某一个节点在若干条线段中出现的次数,时间复杂度为O(logN)。而未优化的空间复杂度为2N,因此有时需要离散化让空间压缩。
例题
数列区间最大值
题目链接:https://www.acwing.com/problem/content/1272/
ST算法
思路分析:直接暴力求,明显的,最坏情况下时间复杂度为O(nm)=10^11,肯定超时
用ST算法来求,预处理O(nlogn)=10^7,查询O(m*1)=10 ^6不会超时
暴力超时代码:
#include<iostream>
using namespace std;
const int N=100005;
int a[N];
int n,m,x,y;
int main()
{
scanf("%d %d",&n,&m);
for(int i=1;i<=n;i++) cin>>a[i];
for(int i=0;i<m;i++)
{
scanf("%d %d",&x,&y);
int max=0;
for(int j=x;j<=y;j++)
{
if(a[j]>max) max=a[j];
}
printf("%d\n",max);
}
return 0;
}
AC代码:
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const LL N=100005;
LL a[N];
LL n,m,x,y;
LL dp[N][20]; //2^20就足够大于n了
//预处理
void ST()
{
for(LL i=1;i<=n;i++) dp[i][0]=a[i];
for(LL j=1;1<<j<=n;j++)
{
for(LL i=1;i+(1<<j)-1<=n;i++)
{
dp[i][j]=max(dp[i][j-1],dp[i+(1<<(j-1))][j-1]);
}
}
}
//查询
LL query(LL l,LL r)
{
LL t=log2(r-l+1);
return max(dp[l][t],dp[r-(1<<t)+1][t]);
}
int main()
{
scanf("%d %d",&n,&m);
for(LL i=1;i<=n;i++) scanf("%d",&a[i]);
ST();
while(m--)
{
scanf("%d %d",&x,&y);
printf("%d\n",query(x,y));
}
return 0;
}
线段树算法
思路分析:
AC代码:
最敏捷的机器人
题目链接:https://www.acwing.com/problem/content/description/1273/
思路分析:就维护最大值和最小值数组即可
AC代码:
#include<bits/stdc++.h>
using namespace std;
const int N=100005;
typedef long long LL;
LL a[N];
LL Max[N][20]; // 最大值
LL Min[N][20]; //最小值
int n,k;
int main()
{
scanf("%d %d",&n,&k);
for(int i=1;i<=n;i++)
{
scanf("%ld",&a[i]);
Max[i][0]=a[i];
Min[i][0]=a[i];
}
for(int j=1;1<<j<=n;j++)
{
for(int i=1;i+(1<<(j-1))-1<=n;i++)
{
Max[i][j]=max(Max[i][j-1],Max[i+(1<<(j-1))][j-1]);
Min[i][j]=min(Min[i][j-1],Min[i+(1<<(j-1))][j-1]);
}
}
int t=n-k+1;
for(int i=1;i<=t;i++)
{
int l=i,r=i+k-1;
int tmp=log2(k);
printf("%d ",max(Max[l][tmp],Max[r-(1<<tmp)+1][tmp]));
printf("%d\n",min(Min[l][tmp],Min[r-(1<<tmp)+1][tmp]));
}
return 0;
}
天才的记忆
题目链接:https://www.acwing.com/activity/content/problem/content/1795/
ST算法
跟上面两个题代码一样
线段树算法
Frequent values
题目链接:http://poj.org/problem?id=3368
ST算法
思路分析:首先需要对给出的区间进行一下处理,将连续的元素进行连续标号,对于标号后的数组,任意给出一个区间,可以将这个区间看做由两部分组成,前面部分是前一个连续数组遗留下来的一些元素,后面部分是多个属于区间内的连续元素组成的数组,最后取遗留下来的元素个数和后面多个连续数的最大的数量二者的最大值即可,也就是先找到这两部分的分界点:区间[i,j]内的第一个1的位置为k,答案就为max(k - i,RMQ(k,j));

AC代码:
#include<iostream>
#include<stdio.h>
#include<math.h>
using namespace std;
const int N=100005;
int a[N];
int dp[N][20];
int n,q,t,pre,x,y;
void ST()
{
for(int i=1;i<=n;i++) dp[i][0]=a[i];
for(int j=1;1<<j<=n;j++)
{
for(int i=1;i+(1<<j)-1<=n;i++)
{
dp[i][j]=max(dp[i][j-1],dp[i+(1<<(j-1))][j-1]);
}
}
}
int query(int l,int r)
{
t=log2(r-l+1);
return max(dp[l][t],dp[r-(1<<t)+1][t]);
}
int main()
{
while(scanf("%d", &n) && n != 0)
{
scanf("%d",&q);
int pre=-100001;
for(int i=1;i<=n;i++)
{
scanf("%d",&t);
if(t==pre) a[i]=a[i-1]+1;
else a[i]=1;
pre=t;
}
ST();
while(q--)
{
scanf("%d %d",&x,&y);
int l=-1;
for(int i=x;i<=y;i++)
{
if(a[i]==1)
{
l=i;
break;
} //找到第一个1作为区间左部
}
if(l!=-1) printf("%d\n",max(l-x,query(l,y))); //区间内有1
else printf("%d\n",y-x+1); //区间内没有1
}
}
return 0;
}
/*
10 4
1 2 3 4 5 6 7 8 9 10 //下标
-1 -1 1 1 1 1 3 10 10 10 //所给数组
1 2 1 2 3 4 1 1 2 3 //连续标号后的数组
2 3 --1 待求区间内只有一组连续重复值,前面有上一组剩下的一个元素
1 10 -- 4 待求区间内有多组连续重复值,前面没有上一个组剩下的一些元素
5 10 --3 待求区间内有多组连续重复值,前面有上一组剩下的两个元素
4 6 --3 待求区间内没有新的连续重复值,只有前面上一组剩下的元素
0
*/
线段树算法
总结(ST和线段树对比)
当题目是离线的时侯使用ST算法更快,时间复杂度为O(nlogn),当题目是在线的时候直接使用线段树维护即可,因为线段树可以进行修改,单点修改维护也是logn,总的时间复杂度为O(nlogn+mlogn)