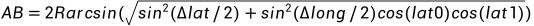参考：

Https://blog.csdn.net/u011339749/article/details/125048180

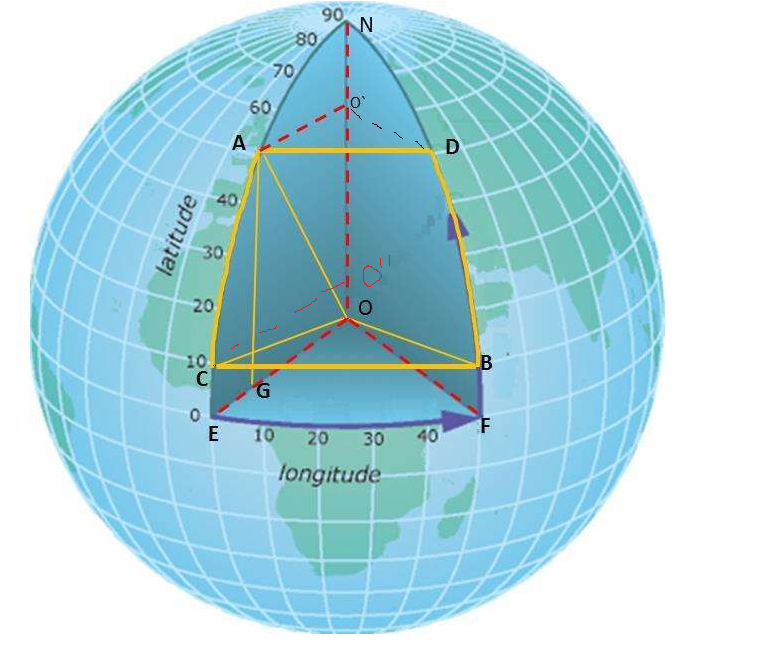
任意两点对应的经纬度A(lat0,long0),B(lat1,long1)

则C(lat1,long0),D(lat0,long1)。通过A、B、C、D四个点可以确定一个四边形平面。同一纬度相互平行，可知连接ACBD四点构成了一个等腰梯形。

设地球半径R，

AO'=Rcos(lat0)，其中lat0是A点的纬度

△AO'D中∠AO'D=long1-long0=∆long,

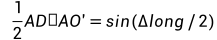
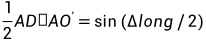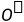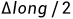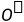 注释：这里AD的一半可以连一条辅助线从到AD交点假设为X0，就是∠AX0的角度

AD=2AO'sin(∆long/2)=2Rcos(lat0)sin(∆long/2)

同理：CO''=Rcos(lat1)   ，即R是CO那条边

再三角形CO''B

CB=2CO''sin(∆long)=2Rcos(lat1)sin(∆long/2)

∠AOC=lat0-lat1=∆lat

从O点连辅助线到AC，交点为X，则∠AOX为∆lat，由于AO=CO（都是地球半径），则AX=AC，那么AX=AOsin(∆lat),即AX=Rsin(∆lat)则AC=2AX=2Rsin(∆lat)

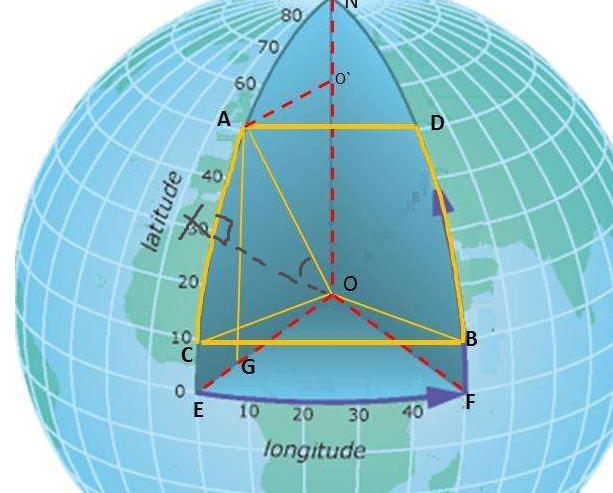
可知:AC=BD=2Rsin(∆lat/2)

现在求AB的长度，得知AB的长度后，可以求得对应的圆心角，进而求得

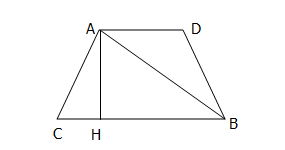
由于ACBD是等腰四边形，那么建立辅助线，可知AGHF是矩形，因此，AG=HF，AD=2AG，CB=2CF

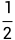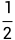则CH=CF-HF=CF-AG=CB-AD=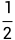（CB-AD)

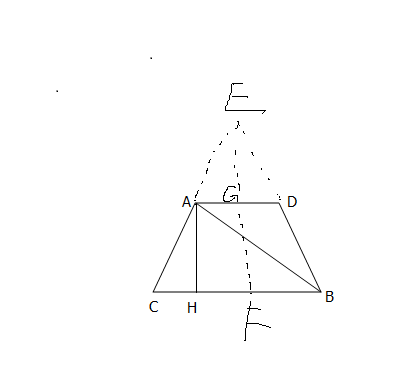
因此可得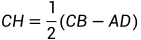

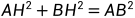
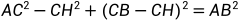
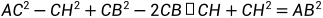
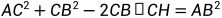
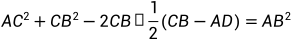
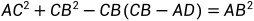
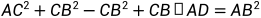
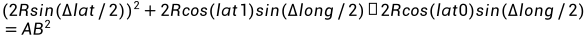
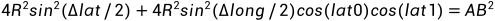
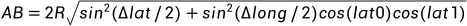
求得AB的长度，这时，只要求得AOB，即以AB为弦的同心圆的圆心角，从而求得（A到B那段圆形的长度,即弧度）

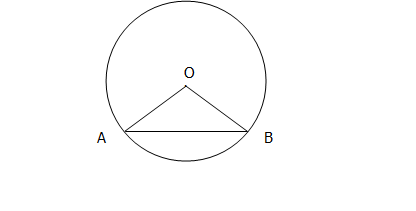
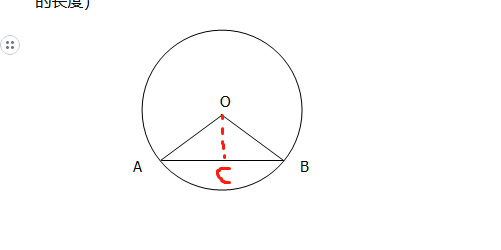
sin(∠AOC)=AC:AO=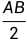:AO=AB:2AO=AB:2R

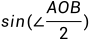=AB:2R

在这里要反三角给出的是弧度值

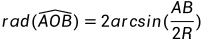
弧度与角度及半径的关系如下：

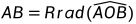
则：

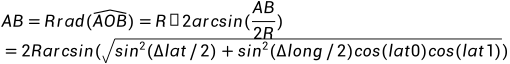
距离公式