写题一点思路也没有，题解也不能看得很懂。

所以系统性的学习DP ing……跟着进度来，因此刷了一些已经刷过的类型的题（也算再次熟悉一下）

P1077 [NOIP2012 普及组] 摆花

题目描述

小明的花店新开张，为了吸引顾客，他想在花店的门口摆上一排花，共 mm 盆。通过调查顾客的喜好，小明列出了顾客最喜欢的 nn 种花，从 11 到 nn 标号。为了在门口展出更多种花，规定第 ii 种花不能超过 a_iai 盆，摆花时同一种花放在一起，且不同种类的花需按标号的从小到大的顺序依次摆列。

试编程计算，一共有多少种不同的摆花方案。

输入格式

第一行包含两个正整数 nn 和 mm，中间用一个空格隔开。

第二行有 nn 个整数，每两个整数之间用一个空格隔开，依次表示 a_1,a_2, \cdots ,a_na1,a2,⋯,an。

输出格式

一个整数，表示有多少种方案。注意：因为方案数可能很多，请输出方案数对 10^6+7106+7 取模的结果。

输入输出样例

输入 #1复制

2 4

3 2

输出 #1复制

2

说明/提示

【数据范围】

对于 20\%20% 数据，有 0<n \le 8,0<m \le 8,0 \le a_i \le 80<n≤8,0<m≤8,0≤ai≤8。

对于 50\%50% 数据，有 0<n \le 20,0<m \le 20,0 \le a_i \le 200<n≤20,0<m≤20,0≤ai≤20。

对于 100\%100% 数据，有 0<n \le 100,0<m \le 100,0 \le a_i \le 1000<n≤100,0<m≤100,0≤ai≤100。

NOIP 2012 普及组 第三题

#include<stdio.h>
#include<string.h>
#include<stdlib.h>
#include<math.h>
int min_(int x,int y)
{
    return x>y?y:x;
}
int main()
{
    int n,m,a[105],dp[105][105]={0};
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++)
    {
        scanf("%d",a+i);
    }
    dp[0][0]=1;
    for(int i=1;i<=n;i++)//花种类的遍历
    {
        for(int j=0;j<=m;j++)//盆数的递增
        {
            for(int k=0;k<=min_(j,a[i]);k++)//k不能超过j和a[i];
            {
                dp[i][j]+=dp[i-1][j-k];
                dp[i][j]%=1000007;
            }
        }
    }
    printf("%d",dp[n][m]);
}

不同路径

题目描述：

一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为 “Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish” ）。

问总共有多少条不同的路径？

示例 1：

输入：m = 3, n = 7

输出：28

示例 2：

输入：m = 3, n = 2

输出：3

解释：

从左上角开始，总共有 3 条路径可以到达右下角。

1. 向右 -> 向下 -> 向下

2. 向下 -> 向下 -> 向右

3. 向下 -> 向右 -> 向下

示例 3：

输入：m = 7, n = 3

输出：28

示例 4：

输入：m = 3, n = 3

输出：6

提示：

• 1 <= m, n <= 100

• 题目数据保证答案小于等于 2 * 109

思路：和昨天的过河卒一模一样，比那个简单多了。首先我们找他的状态转移方程，坐标为(i,j)的点的路径数为a[i][j]=a[i-1][j]+a[i][j-1];再判断一下边界即可。昨天的总结有更详细的解释

代码如下：

int uniquePaths(int m, int n)
{
    int dp[101][101];
    int i=1,j=1;
    for(i=1;i<=n;i++)
    {
        for(j=1;j<=m;j++)
        {
            if(i==1&&j==1)
            {
                dp[i][j]=1;
            } else
            if(i==1&&j>1)判断上边界
            {
                dp[i][j]=dp[i][j-1];
            } else
            if(i>1&&j==1)//判断左边界
            {
                dp[i][j]=dp[i-1][j];
            }
            else dp[i][j]=dp[i-1][j]+dp[i][j-1];
        }
    }
    return dp[n][m];
}

使用最小花费爬楼梯

题目描述

给你一个整数数组 cost ，其中 cost[i] 是从楼梯第 i 个台阶向上爬需要支付的费用。一旦你支付此费用，即可选择向上爬一个或者两个台阶。

你可以选择从下标为 0 或下标为 1 的台阶开始爬楼梯。

请你计算并返回达到楼梯顶部的最低花费。

示例 1：

输入：cost = [10,15,20]

输出：15

解释：你将从下标为 1 的台阶开始。

- 支付 15 ，向上爬两个台阶，到达楼梯顶部。

总花费为 15 。

示例 2：

输入：cost = [1,100,1,1,1,100,1,1,100,1]

输出：6

解释：你将从下标为 0 的台阶开始。

- 支付 1 ，向上爬两个台阶，到达下标为 2 的台阶。

- 支付 1 ，向上爬两个台阶，到达下标为 4 的台阶。

- 支付 1 ，向上爬两个台阶，到达下标为 6 的台阶。

- 支付 1 ，向上爬一个台阶，到达下标为 7 的台阶。

- 支付 1 ，向上爬两个台阶，到达下标为 9 的台阶。

- 支付 1 ，向上爬一个台阶，到达楼梯顶部。

总花费为 6 。

提示：

• 2 <= cost.length <= 1000

• 0 <= cost[i] <= 999

思路:第一步确定dp数组的含义:第二步：我们找状态转移方程：楼梯的步数有俩个来源，下一个楼梯，下俩个楼梯，也就是f[i]=min(f[i-1],f[i-2]);第三步dp数组的初始化，dp[0]=const[0],dp[1]=cost[1];

第四步，确定遍历顺序，从2开始。

代码如下

int minCostClimbingStairs(int* cost, int costSize)
{
    int min(int x,int y)
    {
        return x>y?y:x;
    }
    int dp[1005];//dp数组初始化
    dp[0]=cost[0];
    dp[1]=cost[1];
    for(int i=2;i<costSize;i++)
    {
        dp[i]=min(dp[i-1],dp[i-2])+cost[i];
    }
    return min(dp[costSize-1],dp[costSize-2]);//最后俩个选其中大的那个
}

整数拆分

题目描述：

给定一个正整数 n ，将其拆分为 k 个 正整数 的和（ k >= 2 ），并使这些整数的乘积最大化。

返回 你可以获得的最大乘积 。

示例 1:

输入: n = 2

输出: 1

解释: 2 = 1 + 1, 1 × 1 = 1。

示例 2:

输入: n = 10

输出: 36

解释: 10 = 3 + 3 + 4, 3 × 3 × 4 = 36。

提示:

• 2 <= n <= 58

思路：第一步我们确定dp[i]的含义：分解i的最大乘积，第二步我们找状态转移方程

dp[i]=max(dp[i],max(dp[i-j]*j,(i-j)*i);第三步dp数组的初始化dp[2]=1；第四步确定遍历顺序，也就是从3开始。

code：

int integerBreak(int n)
{
    int max(int x,int y)
    {
        return x>y?x:y;
    }
    int dp[65]={0};dp[2]=1;//2可以拆分为1*1=1
    for(int i=3;i<=n;i++)//从3开始遍历
    {
        for(int j=1;j<i-1;j++)
        {
            dp[i]=max(dp[i],max(dp[i-j]*j,(i-j)*j));
        }
    }
    return dp[n];
}

不同的二叉搜索树

题目描述

给你一个整数 n ，求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种？返回满足题意的二叉搜索树的种数。

示例 1：

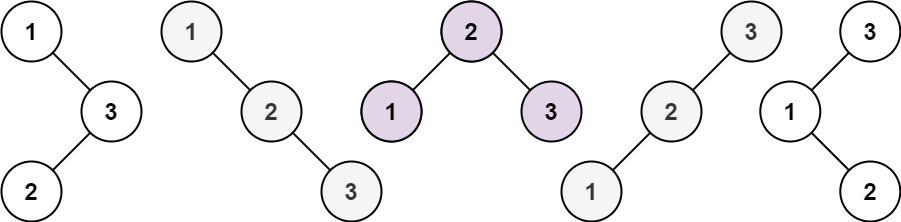
输入：n = 3

输出：5

示例 2：

输入：n = 1

输出：1

提示：

• 1 <= n <= 19

思路：第一步我们确定dp数组的含义：1到i为节点组成的⼆叉搜索树的个数为dp[i]。。第二步我们找状态转移方程：dp[i]+=dp[j-1]*dp[i-j]（笛卡尔积）;第三步我们对dp数组初始化：dp[0]=1,dp[1]=1(i=0时为空树也是一棵树)，第四步确定遍历顺序；从i=2开始。

笛卡尔积粗略解释：

举例而言，若创建以 3 为根、长度为 7 的不同二叉搜索树，整个序列是 [1, 2, 3, 4, 5, 6, 7] ，我们需要从左子序列 [1, 2，] 构建左子树，从右子序列 [4, 5, 6, 7] 构建右子树，然后将它们组合（即笛卡尔积）。

code:

class Solution 
{
public:
    int numTrees(int n) 
    {
        vector<int> dp(n+1);
        dp[1]=1;
        dp[0]=1;
        for(int i=2;i<=n;i++)
        {
            for(int j=1;j<=i;j++)
            {
                dp[i]+=dp[j-1]*dp[i-j];
            }
        }
        return dp[n];
    }
};