题目

给你一个字符串 s 和一个字符规律 p，请你来实现一个支持 ‘.’ 和 ‘*’ 的正则表达式匹配。

‘.’ 匹配任意单个字符
‘*’ 匹配零个或多个前面的那一个元素
所谓匹配，是要涵盖 整个 字符串 s的，而不是部分字符串。

思路

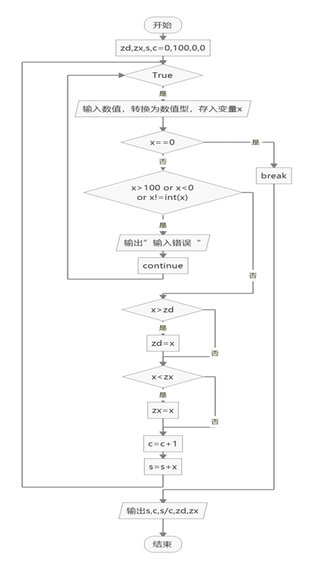
对于字符串p来说，可以有三种字符：

• 普通字符：
• '.'：能够匹配s中同一位置的任意字符
• '*' ：不能单独使用，必须和前一个字符搭配使用，能够匹配s中同一位置字符任意次（包括0次，即把前面的字符消除掉）

即关键是当出现了a*这种字符的时候，到底是匹配几个a

动态规划：

• 定义dp数组：f(i,j) 代表考虑 s 中以 i 为结尾的子串和 p 中的 j 为结尾的子串是否匹配。即最终要求的结果为 f[n][m]
• 确定递推公式：如何求得f(i,j)，这里一共分成三种情况
  （1）p[j] 为普通字符：匹配的条件是前面的字符匹配，同时 s 中的第 i 个字符和 p 中的第 j 位相同，即 f(i,j) = f(i - 1, j - 1) && s[i] == p[j]
  （2）p[j] 为 '.'：匹配的条件是前面的字符匹配， s 中的第 i 个字符可以是任意字符。即 f(i,j) = f(i - 1, j - 1) && p[j] == '.'
  （3）p[j] 为 '*'：往前读取 p[j - 1] 的字符，例如为字符 a；然后根据 a* 实际匹配 s 中 a 的个数是 0 个、1 个、2 个 …
  （3.1）当匹配为 0 个：f(i,j) = f(i, j - 2)
  （3.2）当匹配为 1 个：f(i,j) = f(i - 1, j - 2) && (s[i] == p[j - 1] || p[j - 1] == '.')
  （3.3）当匹配为 2 个：f(i,j) = f(i - 2, j - 2) && ((s[i] == p[j - 1] && s[i - 1] == p[j - 1]) || p[j - 1] == '.')

最后对于*到底匹配多少个a这个过程，对它进行一个简化过程

java代码如下：

class Solution {
    public boolean isMatch(String ss, String pp) {
        // 技巧：往原字符头部插入空格，这样得到 char 数组是从 1 开始，而且可以使得 f[0][0] = true，可以将 true 这个结果滚动下去
        int n = ss.length(), m = pp.length();
        ss = " " + ss;
        pp = " " + pp;
        char[] s = ss.toCharArray(), p = pp.toCharArray();
        // f(i,j) 代表考虑 s 中的 1~i 字符和 p 中的 1~j 字符 是否匹配
        boolean[][] f = new boolean[n + 1][m + 1];
        f[0][0] = true;
        for (int i = 0; i <= n; i++) {
            for (int j = 1; j <= m; j++) {
                // 如果下一个字符是 '*'，则代表当前字符不能被单独使用，跳过
                if (j + 1 <= m && p[j + 1] == '*') continue;
                
                if (i - 1 >= 0 && p[j] != '*') {
                    // 对应了 p[j] 为普通字符和 '.' 的两种情况
                    f[i][j] = f[i - 1][j - 1] && (s[i] == p[j] || p[j] == '.');
                } else if (p[j] == '*') {
                    // 对应了 p[j] 为 '*' 的情况
                    f[i][j] = (j - 2 >= 0 && f[i][j - 2]) || (i - 1 >= 0 && f[i - 1][j] && (s[i] == p[j - 1] || p[j - 1] == '.'));
                }
            }
        }
        return f[n][m];
    }
}

这里附上一个便于理解的版本：

没有降维，如果空间复杂度没有要求，这么写就行，比较好理解

class Solution {
    public boolean isMatch(String s, String p) {
        char[] cs = s.toCharArray();
        char[] cp = p.toCharArray();

        // dp[i][j]:表示s的前i个字符，p的前j个字符是否能够匹配
        boolean[][] dp = new boolean[cs.length + 1][cp.length + 1];

        // 初期值
        // s为空，p为空，能匹配上
        dp[0][0] = true;
        // p为空，s不为空，必为false(boolean数组默认值为false，无需处理)

        // s为空，p不为空，由于*可以匹配0个字符，所以有可能为true
        for (int j = 1; j <= cp.length; j++) {
            if (cp[j - 1] == '*') {
                dp[0][j] = dp[0][j - 2];
            }
        }

        // 填格子
        for (int i = 1; i <= cs.length; i++) {
            for (int j = 1; j <= cp.length; j++) {
                // 文本串和模式串末位字符能匹配上
                if (cs[i - 1] == cp[j - 1] || cp[j - 1] == '.') {
                    dp[i][j] = dp[i - 1][j - 1];
                } else if (cp[j - 1] == '*') { // 模式串末位是*
                    // 模式串*的前一个字符能够跟文本串的末位匹配上
                    if (cs[i - 1] == cp[j - 2] || cp[j - 2] == '.') {
                        dp[i][j] = dp[i][j - 2]      // *匹配0次的情况
                                || dp[i - 1][j];     // *匹配1次或多次的情况
                    } else { // 模式串*的前一个字符不能够跟文本串的末位匹配
                        dp[i][j] = dp[i][j - 2];     // *只能匹配0次
                    }
                }
            }
        }
        return dp[cs.length][cp.length];
    }
}