文章目录
- 题目链接
- 题目大意
- 解题思路
- 代码(C++)
- 动态规划
- 记忆化搜索
题目链接
点我(^_^)
题目大意
注意不是两个概率加和除以2


解题思路
考虑动态规划,因为汤的分配都是以 25 的倍数进行分配的,所以这里把 25 ml 的汤看作一份, 总 的 份 数 = ⌈ 汤 的 体 积 / 25 ⌉ 总的份数 = \left \lceil 汤的体积/25 \right \rceil 总的份数=⌈汤的体积/25⌉,比如 101 ml 的汤可以看作 5 份。
d p [ i ] [ j ] dp[i][j] dp[i][j] 表示在 A 类型汤剩余 i i i 份,B 类型汤剩余 j j j 时,汤A 先分配完的概率 + 汤A和汤B 同时分配完的概率 / 2。那么其递推公式如下,就是分别执行四种分配操作。
d p [ i ] [ j ] = d p [ i − 4 ] [ j ] + d p [ i − 3 ] [ j − 1 ] + d p [ i − 2 ] [ j − 2 ] + d p [ i − 1 ] [ j − 3 ] 4 dp[i][j]=\frac{dp[i-4][j]+dp[i-3][j-1]+dp[i-2][j-2]+dp[i-1][j-3]}{4} dp[i][j]=4dp[i−4][j]+dp[i−3][j−1]+dp[i−2][j−2]+dp[i−1][j−3]
下面考虑起始状态:
- d p [ 0 ] [ 0 ] = 0.5 dp[0][0]=0.5 dp[0][0]=0.5 此时 汤A和汤B 同时分配完的概率为 1,除以 2 之后就是 0.5。
- d p [ i ] [ 0 ] = 0 dp[i][0]=0 dp[i][0]=0 此时 汤B 先被分配完的概率为 1,那么其他情况概率就是 0。
- d p [ 0 ] [ j ] = 0 dp[0][j]=0 dp[0][j]=0 此时 汤A 先被分配完的概率为 1。
此时时间复杂度为 O(n2/125),肯定是不行的, 我们可以发现,每次分配操作有 (4,0),(3,1),(2,2),(1,3) 四种,那么在一次分配中,汤 A 平均会被分配的份数期望为 E(A)=(4+3+2+1)×0.25=2.5,汤 B 平均会被分配的份数期望为 E(B)=(0+1+2+3)×0.25=1.5。因此在 n 非常大的时候,汤 A 会有很大的概率比 B 先分配完,汤 A 被先取完的概率应该非常接近 1。事实上,当我们进行实际计算时发现,当 n≥4475 时,所求概率已经大于0.99999了(可以通过上面的动态规划方法求出),它和 1 的误差(无论是绝对误差还是相对误差)都小于 10−5。
实际我们在进行测算时发现:
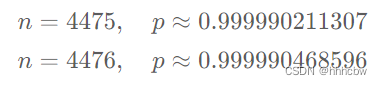
因此在
n
≥
179
×
25
n \ge 179 \times 25
n≥179×25 时,我们只需要输出 1 作为答案即可。在其它的情况下,我们使用动态规划计算出答案。
当然,也可以使用记忆化搜索,这时可以省去计算某些不必要的状态。
代码(C++)
动态规划
class Solution {
public:
double soupServings(int n) {
n = ceil((double) n / 25);
if (n >= 179) {
return 1.0;
}
vector<vector<double>> dp(n + 1, vector<double>(n + 1));
dp[0][0] = 0.5;
for (int i = 1; i <= n; i++) {
dp[0][i] = 1.0;
}
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
dp[i][j] = (dp[max(0, i - 4)][j] + dp[max(0, i - 3)][max(0, j - 1)] +
dp[max(0, i - 2)][max(0, j - 2)] + dp[max(0, i - 1)][max(0, j - 3)]) / 4.0;
}
}
return dp[n][n];
}
};
记忆化搜索
class Solution {
public:
double soupServings(int n) {
n = ceil((double) n / 25);
if (n >= 179) {
return 1.0;
}
memo = vector<vector<double>>(n + 1, vector<double>(n + 1));
return dfs(n, n);
}
double dfs(int a, int b) {
if (a <= 0 && b <= 0) {
return 0.5;
} else if (a <= 0) {
return 1;
} else if (b <= 0) {
return 0;
}
if (memo[a][b] > 0) {
return memo[a][b];
}
memo[a][b] = 0.25 * (dfs(a - 4, b) + dfs(a - 3, b - 1) +
dfs(a - 2, b - 2) + dfs(a - 1, b - 3));
return memo[a][b];
}
private:
vector<vector<double>> memo;
};

![[附源码]java毕业设计校园二手交易平台的设计](https://img-blog.csdnimg.cn/2c1b6ec77e274151964a6bce79b03da6.png)








![[附源码]java毕业设计校园超市进销存管理系统](https://img-blog.csdnimg.cn/6d03989ba7674d859895e9cef26ca113.png)