---

前言

在之前的文章中，我们介绍了对于系统频域上的分析，主要集中在傅里叶变换和Z变换后对于频率响应的分析，包括幅频响应，相位响应和群延迟，并介绍了LTI系统中的幅频响应相同系统、全通系统、最小相位系统等系统。

在接下来的文章中，将会真正的学习在计算机中如何实现傅里叶变换，以及通过傅里叶变换实现之前所介绍的系统。

本篇文章将会介绍新的傅里叶变换——DFT，即离散傅里叶变换的分析和解释，这是一种可以通过数字系统实现的傅里叶变换。然后对于DFT的性质将会做一个归纳。

|版本声明：山河君，未经博主允许，禁止转载

---

一、FT、FS、DTFT、DFS

在以前的文章中，我们介绍过总的傅里叶变换，以及对于DTFT、DFS的详细介绍。而一些傅里叶变换是无法在数字系统中进行实现的。

1.FT和FS

• 傅里叶变换（FT）：用于连续时间信号的频谱分析，通常适用于无限长的信号。由于时域信号是连续的，频域也是连续的，计算机无法直接处理连续的频域，因此我们无法直接应用传统的傅里叶变换进行数值计算。
• 傅里叶级数（FS）：用于分析周期信号，也适用于连续时间的信号，频域由一系列离散的频率分量组成。频谱是离散的，但由于时域信号是连续的，所以计算机处理起来仍然存在困难。

对于FT和FS如同下图，总的来说因为时域是连续的，所以无法在数字系统中进行结算。

2.DTFT和DFS

对于时域连续导致无法在数字系统上计算的问题，在这一系列最开始的文章中音频进阶学习二——模数和数模转换中的采样、量化和编码中就有说过，将模拟信号通过模数转换为离散的数字信号，此时就可以在数字系统上进行计算。

• 离散时间傅里叶变换（DTFT）：是对离散时间信号（无限长）进行傅里叶变换，产生一个连续频域，就像传统的傅里叶变换一样。由于时域是离散的，但频域是连续的，所以仍然不能直接在计算机上进行处理。
• 离散傅里叶级数（DFS）：是对周期离散信号进行傅里叶级数展开，结果是离散频率的频谱。由于信号是周期的，频域也是离散的，但由于序列无限长，因此只能说是计算上是可能的。

对于DTFT和DFS的解析在这系列音频进阶学习九——离散时间傅里叶变换DTFT和音频进阶学习十一——离散傅里叶级数DFS中。

二、DFT定义

1.对于DFT的理解

很明显，数字系统处理的需要是在时域和频域上是离散的，且是有限长的。为了达成这样的条件，延申出了DFT也就是离散傅里叶变换。

那么下面对于DTFT的理解可以从下文的三种角度上来分析：

1）DTFT和DFT

由于DTFT在时域上是离散的，在频域上是在$[-\pi ,\pi ]$上连续，那么如果我们对于频域上再进行采样，那么就可以得到时域离散信号对应的离散的频域。
对于DTFT进行周期采样有：
$$X(e^{j\omega })=\sum _{n=-\infty }^{\infty }x[n]e^{-j\omega n}=>X(k)=X(e^{j\omega }){|}_{\omega =\frac{2\pi k}{N}}=\sum _{n=-\infty }^{\infty }x[n]e^{-j\frac{2\pi kn}{N}}$$
其中

• $X(k)$:是序列的DFT
• $N$:是序列周期
• $k$:表示频率索引，范围是$[0,N-1]$
• $e^{j(\frac{-2\pi kn}{N})}$:复指数，表示信号的频率分量

2）DFS和DFT

对于周期信号而言，我们可以只取一个周期进行分析，这样就避免了无限长序列在数字系统中无法计算的问题。而对于DFT实际上就是周期序列一个周期等间隔取样的频谱。
如下图：

而在表达式上，实际上就是把~去掉
$$\tilde{X}[k]=\sum _{n=0}^{N-1}{e}^{j(\frac{-2\pi kn}{N})}\tilde{x}[n]=>X[k]=\sum _{n=0}^{N-1}{e}^{j(\frac{-2\pi kn}{N})}x[n]$$
$$\tilde{x}[n]=\frac{1}{N}\sum _{k=0}^{N-1}{e}^{j(\frac{2\pi kn}{N})}\tilde{X}[k]=>x[n]=\frac{1}{N}\sum _{k=0}^{N-1}{e}^{j(\frac{2\pi kn}{N})}X[k]$$
所以对于DFT，和DFS存在一样的性质。

3）有限长序列和周期序列

真实采样的信号通常是非周期且无限长的，所以针对于非周期的信号，在时域上进行截断，此时就变成了有限长序列，同时对于截断的时域信号认为它是周期信号来进行分析。
如同下图：

此时非周期序列和周期的序列关系如：
$$\begin{gathered} x[n]=\tilde{x}[n]R_N[n];R_N[n]=\{\begin{array}{l}1,0\le n\le N-1\\ 0,n>N-1||n<0\end{array} \\ \tilde{x}[n]=x[((n){)}_N] \end{gathered}$$
其中$N$是序列周期，$x[((n){)}_N]$表示$n$对于$N$进行取模运算。

但值得注意的是设信号在截断的两端突然变为零，这相当于信号发生了突变，会发生频谱泄露。这个会在以后讲解加窗的文章中进行详细介绍。

2.圆周卷积

1）线性卷积

回顾一下，在音频进阶学习五——求线性时不变系统卷积和的解时，对于系统的输出线性卷积的长度有做过理解：
$$y[n]=\sum _{m=0}^{M-1}x[m]h[n-m]$$
如果系统的输入是有限的$N$，并且系统响应也有有限的为$L$，那么系统的输出长度为$N+L-1$。

2）圆周卷积

圆周卷积是针对于 DFT 计算中出现的一种特殊卷积，它的本质是在有限长度的序列上执行周期性卷积，而不像普通的线性卷积那样在无限长度序列上进行计算。

对于周期序列，当一个信号滑动超过长度$N$ 时，它会绕回到起点，并与最开始的部分重新进行卷积计算。即系统的输入长度为$N$，那么系统的输出长度也是$N$，此时用圆周卷积表示
$$y[n]=\sum _{m=0}^{N-1}x[m]h((n-m)\mathrm{mod}N)$$
其中$(n-m)\mathrm{mod}N$让索引$n-m$始终保持在$[0,N-1]$之内，而不会越过序列长度。

三、频率采样和插值恢复

上文中分析了DTFT与DFT，DFS与DFT的关系。我们知道对于DFT可以看作对于DTFT进行频率采样，又可以看作是DFS的一个周期的分析。接下来我们进一步了解如何进行频率采样，并且如何将采样恢复到DTFT。

1.频率采样的影响

对于序列$x[n]$，如果它是周期为$N$的，那么$X(e^{j\omega })=\tilde{X}[k]$，但如果$x[n]$是非周期，$X(e^{j\omega })$会包含所有的频率分量，而对其进行采样，可能会丢失掉一部分频率分量，如同下图：

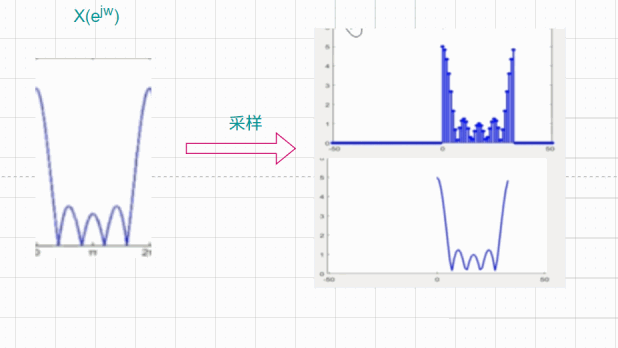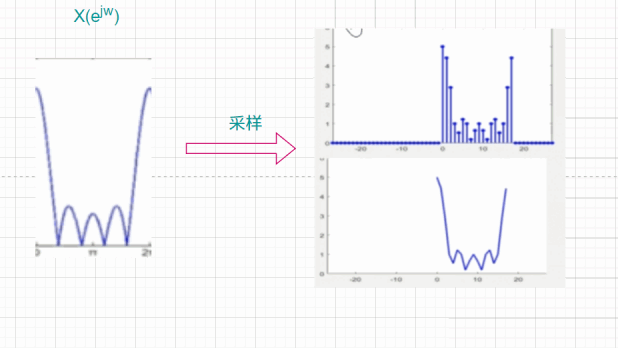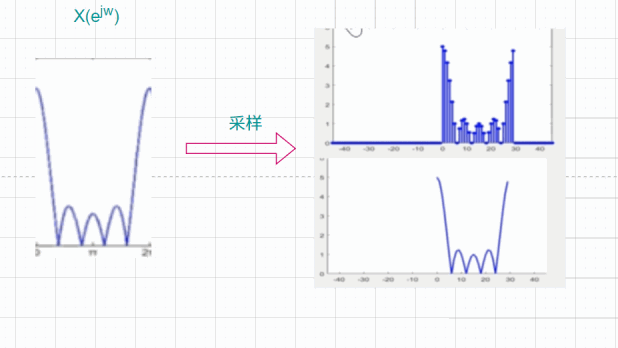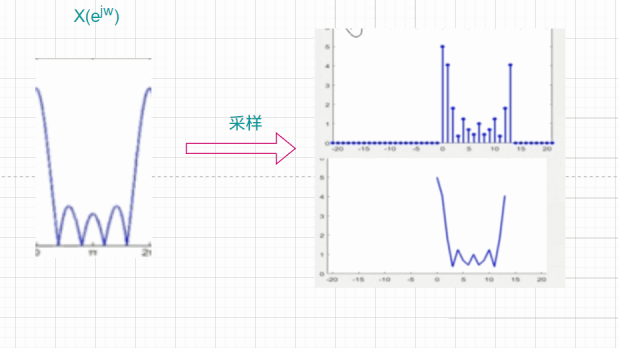
但是可以从上图看出，如果采样越密，那么得到的DFS就越平滑，而对于DFT也就越接近原始序列的DTFT。

2.频率采样和时域序列的关系

1）从频率采样看时域的关系

我们知道DTFT的频域范围是在$[-\pi ,\pi ]$或者说是在$[0,2\pi ]$之间的。在上文中对于DTFT进行采样，采样点数为$N$：
$$X(e^{j\omega }){|}_{\omega =\frac{2\pi k}{N}}=\sum _{n=-\infty }^{\infty }x[n]e^{-j\frac{2\pi kn}{N}}$$
那么实际上是将$2\pi$分为了$N$个等份，$k\in [0,N-1]$，此时认为该序列是一个周期序列，与此对应的时域上序列的周期应该是N，对应的输入序列$x[n]$的长度应该看作是周期信号。

2）从时域截取看频域的关系

如果对于非周期无限长序列$x_a[n]$进行截取$L$（有限长且认为是频域带限），并以$L$为周期进行延拓，那么得到一个周期序列$x[n]$，那么此时通过DTFT得到的是一个在$[0,2\pi ]$之间连续的频域，而DFS是一个无限长离散的离散频域，对于DFT则是有限长且离散的频域，如下图:

3）序列长度L与周期N

从上文可知，此时非周期序列截断后成为长度为$L$的序列$x[n]$，可以表示为：
$$x[n]=\tilde{x}[n]R_N[n];R_N[n]=\{\begin{array}{l}1,0\le n\le L-1\\ 0,n>L-1||n<0\end{array}$$
那么再进行周期延拓可以表示为：
$$\tilde{x}[n]=x[((n){)}_N]$$
其中$N$是序列周期，$x[((n){)}_N]$表示$n$对于$N$进行取模运算。

如果此时对于周期$N$和序列长度$L$不一致会发生什么呢？

• $N\ge L$时：假设频率采样$N=10$，而时域截取为$L=5$，那么系统输出不会有叠加
  

• $N<L$时：假设频率采样$N=10$，而时域截取为$L=11$，那么系统输出会有叠加
  

也就是说，当$N\ge L$时，频域采样不会造成时域混叠。

3.插值恢复

从上文可知，当$N\ge L$时，从DTFT采样到DFT，频域采样不会造成时域混叠。那么此时就可以利用DFT通过插值恢复为DTFT。所以之前为什么可以利用计算机显示DTFT，实际上就是用DFT计算再进行恢复。下面就是通过$X[k]$通过插值核$\frac{\sin \left(\frac{N\omega -2\pi k}{2}\right)}{\sin \left(\frac{N\omega -2\pi k}{2N}\right)}$进行插值，最后再进行相位调整对齐$e^{-j(\omega -\frac{2\pi k}{N})\frac{N-1}{2}}$的推导：

我们知道DTFT和DFT为：
$$\begin{gathered} X(e^{j\omega })=\sum _{n=-\infty }^{\infty }x[n]e^{-j\omega n} \\ x[n]=\frac{1}{N}\sum _{k=0}^{N-1}{e}^{j(\frac{2\pi kn}{N})}X[k] \end{gathered}$$
那么当序列周期周期为$N$，也就是时域截断为$N$时，对于DTFT：
$$X(e^{j\omega })=\sum _{n=-\infty }^{\infty }x[n]e^{-j\omega n}=\sum _{n=-0}^{N-1}x[n]e^{-j\omega n}$$
将DFT时域表示代入
$$\begin{gathered} X(e^{j\omega })=\sum _{n=-0}^{N-1}(\frac{1}{N}\sum _{k=0}^{N-1}{e}^{j(\frac{2\pi kn}{N})}X[k])e^{-j\omega n} \\ =\frac{1}{N}\sum _{n=-0}^{N-1}\sum _{k=0}^{N-1}X[k]e^{j(\frac{2\pi kn}{N})}{e}^{-j\omega n} \\ =\frac{1}{N}\sum _{k=0}^{N-1}X[k]\sum _{n=-0}^{N-1}\left(e^{j(\frac{2\pi kn}{N})}{e}^{-j\omega n}\right) \\ =\frac{1}{N}\sum _{k=0}^{N-1}X[k]\sum _{n=-0}^{N-1}{e}^{-j(\omega -\frac{2\pi k}{N})n} \end{gathered}$$
此时对于${\sum }_{n=-0}^{N-1}{e}^{-j(\omega -\frac{2\pi k}{N})n}$是一个等比数列，那么此时：
$$\frac{1}{N}\sum _{k=0}^{N-1}X[k]\sum _{n=-0}^{N-1}{e}^{-j(\omega -\frac{2\pi k}{N})n}=\frac{1}{N}\sum _{k=0}^{N-1}X[k]\frac{1-e^{-jN(\omega -\frac{2\pi k}{N})}}{1-e^{-j(\omega -\frac{2\pi k}{N})}}$$
将该式分解替换分子分母的1：
$$\frac{1}{N}\sum _{k=0}^{N-1}X[k]\frac{1-e^{-jN(\omega -\frac{2\pi k}{N})}}{1-e^{-j(\omega -\frac{2\pi k}{N})}}=\frac{1}{N}\sum _{k=0}^{N-1}X[k]\frac{(e^{j\frac{N(\omega -\frac{2\pi k}{N})}{2}}-e^{-j\frac{N(\omega -\frac{2\pi k}{N})}{2}})e^{-j\frac{N(\omega -\frac{2\pi k}{N})}{2}}}{\frac{e^{j\frac{(\omega -\frac{2\pi k}{N})}{2}}-e^{-j\frac{(\omega -\frac{2\pi k}{N})}{2}}}{2}{e}^{-j\frac{(\omega -\frac{2\pi k}{N})}{2}}}$$
根据上述公式通过欧拉公式解可得：
$$X(e^{j\omega )}=\frac{1}{N}\sum _{k=0}^{N-1}X[k]\frac{\sin \left(\frac{N\omega -2\pi k}{2}\right)}{\sin \left(\frac{N\omega -2\pi k}{2N}\right)}{e}^{-j(\omega -\frac{2\pi k}{N})\frac{N-1}{2}}$$

四、DFT的性质和定理

结合上文，我们知道对于DFT和DFS有一样的性质和定理，和DTFT有相似的性质，区别是DFT的卷积是一种圆周卷积，这里不做证明只进行列举了。建议是结合对于DTFT、DFS的性质对照理解：音频进阶学习十——DTFT的条件、性质与举例，音频进阶学习十一——离散傅里叶级数DFS。

性质	时域 ( x[n] )	频域 ( X[k] )
线性性质	$a{x}_1[n]+b{x}_2[n]$	$a{X}_1[k]+b{X}_2[k]$
时域循环移位	$x[(n-m)\mathrm{mod}N]$	$e^{-j\frac{2\pi }{N}mk}X[k]$
频域循环移位	$e^{j\frac{2\pi }{N}mn}x[n]$	$X[(k-m)\mathrm{mod}N]$
时间倒置	$x[-n\mathrm{mod}N]$	$X[-k\mathrm{mod}N]$
实信号的对称性	$x[n]$为实数	$X[k]$满足共轭对称$X[N-k]=X^{\ast }[k]$
时域循环卷积	$(x_1⊛x_2)[n]={\sum }_{m=0}^{N-1}{x}_1[m]x_2[(n-m)\mathrm{mod}N]$	$X_1[k]X_2[k]$
频域循环卷积	$x[n]X[k]$	时域的循环卷积
Parseval 定理	$\sum_{n=0}^{N-1}	x[n]
Plancherel 定理	${\sum }_{n=0}^{N-1}{x}_1[n]x_2^{\ast }[n]=\frac{1}{N}{\sum }_{k=0}^{N-1}{X}_1[k]X_2^{\ast }[k]$

其中：

• $⊛$代表 时域的循环卷积： $(x_1⊛x_2)[n]={\sum }_{m=0}^{N-1}{x}_1[m]x_2[(n-m)\mathrm{mod}N]$
• Parseval 定理 说明了 时域和频域的能量守恒关系。
• Plancherel 定理 是 Parseval 定理的更一般形式，涉及 内积关系。

---

总结

本篇文章中介绍了新的傅里叶变换——DFT，这是一种可以在计算机中实现的傅里叶变换。但是值得注意的是，这种变换的计算次数过多，于是会衍生出一种在计算机中快速进行计算的方法FFT——快速傅里叶变换。这也是在下一篇文章中将要学习的变换。

反正收藏也不会看，不如点个赞吧