0 专栏介绍

🔥课设、毕设、创新竞赛必备！🔥本专栏涉及更高阶的运动规划算法轨迹优化实战，包括：曲线生成、碰撞检测、安全走廊、优化建模(QP、SQP、NMPC、iLQR等)、轨迹优化(梯度法、曲线法等)，每个算法都包含代码实现加深理解

🚀详情：运动规划实战进阶：轨迹优化篇

---

本期实现如下的碰撞检测效果

1 凸多边形碰撞检测

在计算机图形学、游戏开发和机器人运动规划中，碰撞检测是保证物体交互真实性的核心技术。凸多边形因其独特的几何特性（任意两点连线均位于图形内部），成为碰撞检测的高效研究对象。与凹多边形相比，凸多边形的碰撞判定可通过分离轴定理（Separating Axis Theorem, SAT）在多项式时间内完成，且无需复杂的三角剖分。本节将通过几何投影原理，揭示如何通过极值投影快速判断两个凸多边形是否相交

2 多边形判凸算法

并非所有多边形都天生为“凸”。判凸算法是碰撞检测的前置关卡，其任务是判断给定多边形的顶点序列是否满足凸性条件，只有凸多边形才能应用分离轴定理进行碰撞检测。

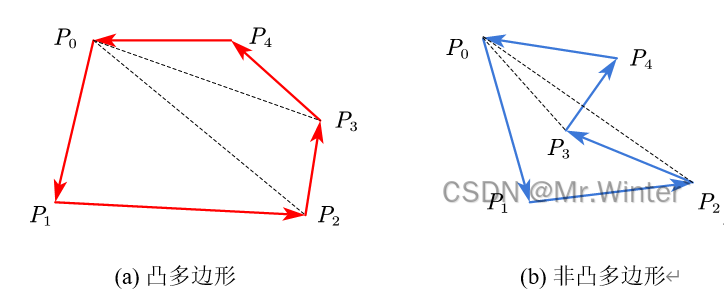
通过向量积可以判断向量的旋转方向。如图所示，由于

$$\overrightarrow{P_1{P}_2}\times \overrightarrow{P_2{P}_3}>0$$

说明从$\overrightarrow{P_1{P}_2}$到$\overrightarrow{P_2{P}_3}$是向左转；由于

$$\overrightarrow{P_2{P}_3}\times \overrightarrow{P_3{P}_4}>0$$

说明从$\overrightarrow{P_2{P}_3}$到$\overrightarrow{P_3{P}_4}$是向右转。若多边形是凸多边形，则向量的选择方向始终同向——逆时针遍历则总是向左转、顺时针遍历则总是向右转。所以在逆时针遍历多边形顶点的过程中，若存在

$$\overrightarrow{P_{i-1}{P}_i}\times \overrightarrow{P_i{P}_{i+1}}<0$$

则表明多边形非凸，否则为凸多边形。

3 分离轴定理(SAT)

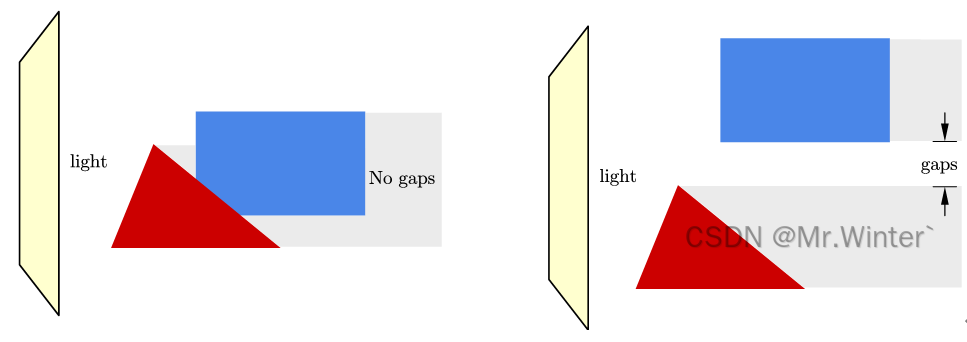
分离轴定理的核心思想直击几何本质：若存在一条直线能将两图形投影分隔，则二者不相交；反之则碰撞。直观地，如下图所示，若两个凸多边形没有发生碰撞，则必存在某角度的光源使两物体的投影存在间隙；也即必存在一条直线使得两个多边形在这条直线上的投影不重叠，这条直线被称为分离轴

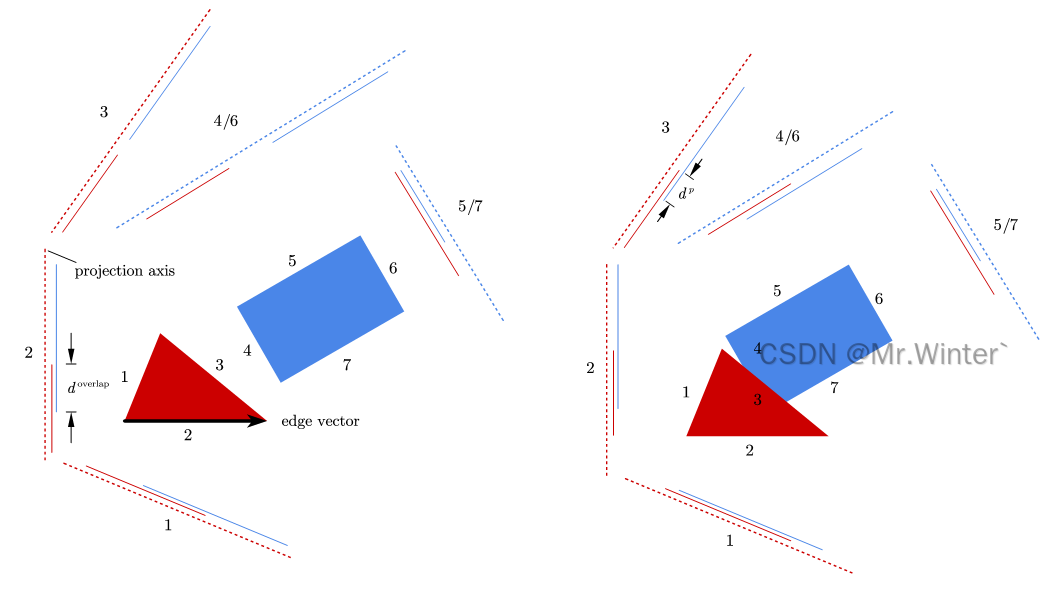
如下图所示，称凸多边形的某条边为边缘向量，平行于边缘向量法向的直线称为投影轴。所有投影轴组成投影轴集合$P$，$|P|$等于两个凸多边形的边数之和。遍历$P$中的每条投影轴${\mathbf{p}}_i$，将两个多边形分别投影到${\mathbf{p}}_i$上得到两个投影线段，其重叠区域的长度称为重叠深度$d_i^{\mathrm{o}\mathrm{v}\mathrm{e}\mathrm{r}\mathrm{l}\mathrm{a}\mathrm{p}}$。定义穿透深度

$$d^p=\underset{i}{\min }\left\{d_i^{\mathrm{o}\mathrm{v}\mathrm{e}\mathrm{r}\mathrm{l}\mathrm{a}\mathrm{p}}\right\}$$

若$d^p=0$则两个凸多边形没有发生碰撞；若$d^p>0$则两凸多边形存在碰撞，其中$d^p$所在的投影轴称为穿透向量或分离向量，将其中一个多边形沿分离向量运动$d^p$个单位可以最快消除碰撞。

分离轴定理的算法流程如下所示

4 算法仿真与可视化

4.1 核心算法

首先，找到两个待检测多边形的分离轴。分离轴平行于边缘法向量，其位置不限，因为其长度是无限的，该轴的方向才是关键

std::vector<Ogre::Vector3> axes;
for (int i = 0; i < size(); ++i)
{
  const auto& pt1 = points_[i];
  const auto& pt2 = points_[next(i)];
  const auto& edge = pt2 - pt1;
  Ogre::Vector3 nor(edge.y, -edge.x, 0.0);
  nor.normalise();
  axes.emplace_back(std::move(nor));
}

for (int i = 0; i < other->size(); ++i)
{
  const auto& pt1 = other->points()[i];
  const auto& pt2 = other->points()[other->next(i)];
  const auto& edge = pt2 - pt1;
  Ogre::Vector3 nor(edge.y, -edge.x, 0.0);
  nor.normalise();
  axes.emplace_back(std::move(nor));
}

接着，对每一条分离轴计算两个多边形在该轴的投影。通过将一个多边形上的每个顶点向量，与选定的投影轴进行点积，然后保留该多边形在该投影轴上所有投影中的最大值和最小值，即可表示一个多边形在某投影轴上的投影

double proj_1_min, proj_1_max;
double proj_2_min, proj_2_max;
project(points_, axis, proj_1_min, proj_1_max);
project(other->points(), axis, proj_2_min, proj_2_max);

只要存在一条分离轴使两个多边形的投影不重合，即表明不发生碰撞

if (!(proj_1_min <= proj_2_max && proj_2_min <= proj_1_max))
{
  return false;
}

4.2 仿真实验

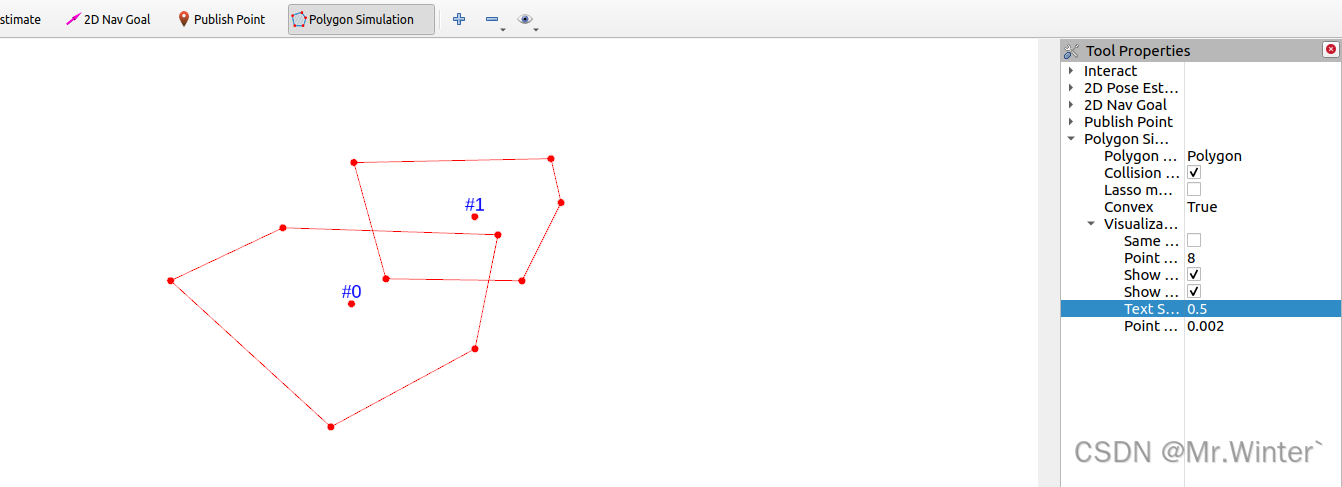
通过Rviz->Add New Tool添加Polygon Simulation插件

开启碰撞检测功能后验证凸多边形的相交检测功能

• 未相交情形

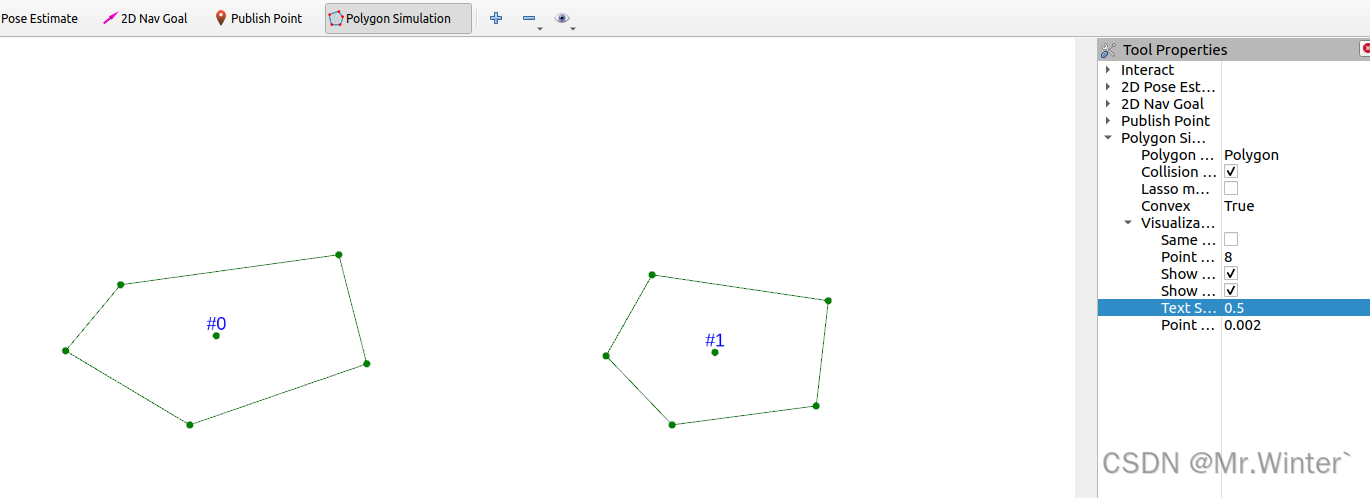
• 相交情形

完整工程代码请联系下方博主名片获取

---

🔥 更多精彩专栏：

• 《ROS从入门到精通》
• 《Pytorch深度学习实战》
• 《机器学习强基计划》
• 《运动规划实战精讲》
• …

👇源码获取 · 技术交流 · 抱团学习 · 咨询分享 请联系👇