机器学习算法 - 随机森林之决策树初探（1）

news2025/4/3 1:32:26

随机森林是基于集体智慧的一个机器学习算法，也是目前最好的机器学习算法之一。

随机森林实际是一堆决策树的组合（正如其名，树多了就是森林了）。在用于分类一个新变量时，相关的检测数据提交给构建好的每个分类树。每个树给出一个分类结果，最终选择被最多的分类树支持的分类结果。回归则是不同树预测出的值的均值。

要理解随机森林，我们先学习下决策树。

决策树 - 把你做选择的过程呈现出来

决策树是一个很直观的跟我们日常做选择的思维方式很相近的一个算法。

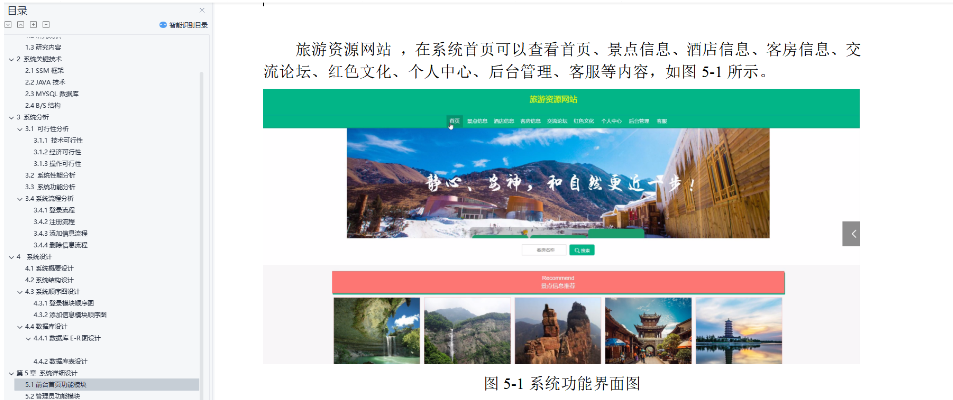
如果有一个数据集如下：

data <- data.frame(x=c(0,0.5,1.1,1.8,1.9,2,2.5,3,3.6,3.7), color=c(rep('blue',5),rep('green',5)))
data

##      x color
## 1  0.0  blue
## 2  0.5  blue
## 3  1.1  blue
## 4  1.8  blue
## 5  1.9  blue
## 6  2.0 green
## 7  2.5 green
## 8  3.0 green
## 9  3.6 green
## 10 3.7 green

那么假如加入一个新的点，其x值为1，那么该点对应的最可能的颜色是什么？

根据上面的数据找规律，如果x<2.0则对应的点颜色为blue，如果x>=2.0则对应的点颜色为green。这就构成了一个只有一个决策节点的简单决策树。

决策树常用来回答这样的问题：给定一个带标签的数据集(标签这里对应我们的color列)，怎么来对新加入的数据集进行分类?

如果数据集再复杂一些，如下，

data <- data.frame(x=c(0,0.5,1.1,1.8,1.9,2,2.5,3,3.6,3.7),
                   y=c(1,0.5,1.5,2.1,2.8,2,2.2,3,3.3,3.5),
                   color=c(rep('blue',3),rep('red',2),rep('green',5)))

data

##      x   y color
## 1  0.0 1.0  blue
## 2  0.5 0.5  blue
## 3  1.1 1.5  blue
## 4  1.8 2.1   red
## 5  1.9 2.8   red
## 6  2.0 2.0 green
## 7  2.5 2.2 green
## 8  3.0 3.0 green
## 9  3.6 3.3 green
## 10 3.7 3.5 green

如果x>=2.0则对应的点颜色为green。
如果x<2.0则对应的点颜色可能为blue，也可能为red。

这时就需要再加一个新的决策节点，利用变量y的信息。

这就是决策树，也是我们日常推理问题的一般方式。

训练决策树 - 确定决策树的根节点

第一个任务是确定决策树的根节点：选择哪个变量和对应阈值选择多少能给数据做出最好的区分。

比如上面的例子，我们可以先处理变量x，选择阈值为2 (为什么选2，是不是有比2更合适阈值，我们后续再说)，则可获得如下分类：

我们也可以先处理变量y，选择阈值为2，则可获得如下分类：

那实际需要选择哪个呢？

实际我们是希望每个选择的变量和阈值能把不同的类分的越开越好；上面选择变量x分组时，Green完全分成一组；下面选择y分组时，Blue完全分成一组。怎么评价呢？

这时就需要一个评价指标，常用的指标有Gini inpurity和Information gain。

Gini Impurity

在数据集中随机选择一个数据点，并随机分配给它一个数据集中存在的标签，分配错误的概率即为Gini impurity。

我们先看第一套数据集，10个数据点，5个blue，5个green。从中随机选一个数据点，再随机选一个分类标签作为这个数据点的标签，分类错误的概率是多少？如下表，错误概率为0.25+0.25=0.5(看下面的计算过程)。

probility <- data.frame(Event=c("Pick Blue, Classify Blue",
                                "Pick Blue, Classify Green",
                                "Pick Green, Classify Blue",
                                "Pick Green, Classify Green"), 
                        Probability=c(5/10 * 5/10, 5/10 * 5/10, 5/10 * 5/10, 5/10 * 5/10),
                        Type=c("Blue" == "Blue",
                               "Blue" == "Green",
                               "Green" == "Blue",
                               "Green" == "Green"))
probility

##                        Event Probability  Type
## 1   Pick Blue, Classify Blue        0.25  TRUE
## 2  Pick Blue, Classify Green        0.25 FALSE
## 3  Pick Green, Classify Blue        0.25 FALSE
## 4 Pick Green, Classify Green        0.25  TRUE

我们再看第二套数据集，10个数据点，2个red，3个blue，5个green。从中随机选一个数据点，再随机选一个分类标签作为这个数据点的标签，分类错误的概率是多少？0.62。

probility <- data.frame(Event=c("Pick Blue, Classify Blue",
                                "Pick Blue, Classify Green",
                                "Pick Blue, Classify Red",
                                "Pick Green, Classify Blue",
                                "Pick Green, Classify Green",
                                "Pick Green, Classify Red",
                                "Pick Red, Classify Blue",
                                "Pick Red, Classify Green",
                                "Pick Red, Classify Red"
                              ),
                        Probability=c(3/10 * 3/10, 3/10 * 5/10, 3/10 * 2/10, 
                                      5/10 * 3/10, 5/10 * 5/10, 5/10 * 2/10,
                                      2/10 * 3/10, 2/10 * 5/10, 2/10 * 2/10),
                        Type=c("Blue" == "Blue",
                               "Blue" == "Green",
                               "Blue" == "Red",
                               "Green" == "Blue",
                               "Green" == "Green",
                               "Green" == "Red",
                               "Red" == "Blue",
                               "Red" == "Green",
                               "Red" == "Red"
                               ))
probility

##                        Event Probability  Type
## 1   Pick Blue, Classify Blue        0.09  TRUE
## 2  Pick Blue, Classify Green        0.15 FALSE
## 3    Pick Blue, Classify Red        0.06 FALSE
## 4  Pick Green, Classify Blue        0.15 FALSE
## 5 Pick Green, Classify Green        0.25  TRUE
## 6   Pick Green, Classify Red        0.10 FALSE
## 7    Pick Red, Classify Blue        0.06 FALSE
## 8   Pick Red, Classify Green        0.10 FALSE
## 9     Pick Red, Classify Red        0.04  TRUE

Wrong_probability = sum(probility[!probility$Type,"Probability"])
Wrong_probability

## [1] 0.62

Gini Impurity计算公式：

假如我们的数据点共有C个类，p(i)是从中随机拿到一个类为i的数据，Gini Impurity计算公式为：

$$ G = \sum_{i=1}^{C} p(i)*(1-p(i)) $$

对第一套数据集，10个数据点，5个blue，5个green。从中随机选一个数据点，再随机选一个分类标签作为这个数据点的标签，分类错误的概率是多少？错误概率为0.25+0.25=0.5。

对第二套数据集，10个数据点，2个red，3个blue，5个green。

从中随机选一个数据点，再随机选一个分类标签作为这个数据点的标签，分类错误的概率是多少？0.62。

决策树分类后的Gini Impurity

对第一套数据集来讲，按照x<2分成两个分支，各个分支都只包含一个分类数据，各自的Gini IMpurity值为0。

这是一个完美的决策树，把Gini Impurity为0.5的数据集分类为2个Gini Impurity为0的数据集。Gini Impurity== 0是能获得的最好的分类结果。

第二套数据集，我们有两种确定根节点的方式，哪一个更优呢？

我们可以先处理变量x，选择阈值为2，则可获得如下分类：

每个分支的Gini Impurity可以如下计算：

当前决策的Gini impurity需要对各个分支包含的数据点的比例进行加权，即

我们也可以先处理变量y，选择阈值为2，则可获得如下分类：

每个分支的Gini Impurity可以如下计算：

当前决策的Gini impurity需要对各个分支包含的数据点的比例进行加权，即

两个数值比较0.24<0.29，选择x作为第一个分类节点是我们第二套数据第一步决策树的最佳选择。

前面手算单个变量、单个分组不算麻烦，也是个学习的过程。后续如果有更多变量和阈值时，再手算就不合适了。下一篇我们通过暴力方式自写函数训练决策树。

当前计算的结果，可以作为正对照，确定后续函数结果的准确性。（NBT：你想成为计算生物学家？）

参考：

https://victorzhou.com/blog/intro-to-random-forests/
https://victorzhou.com/blog/gini-impurity/
https://stats.stackexchange.com/questions/192310/is-random-forest-suitable-for-very-small-data-sets
https://towardsdatascience.com/understanding-random-forest-58381e0602d2
https://www.stat.berkeley.edu/~breiman/RandomForests/reg_philosophy.html
https://medium.com/@williamkoehrsen/random-forest-simple-explanation-377895a60d2d