【线性代数】1行列式

news2025/2/19 16:10:59

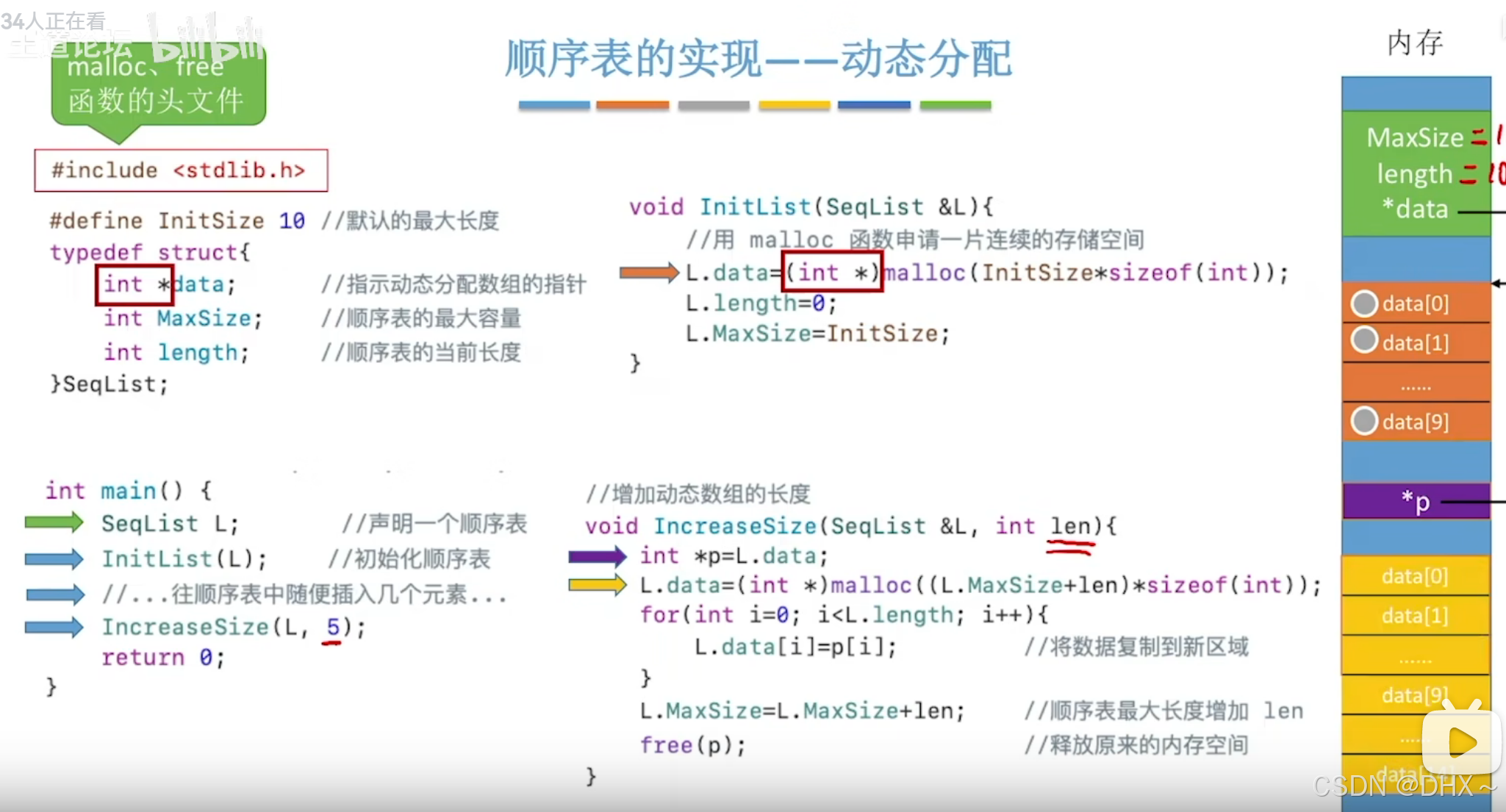
1. 行列式的概念

行列式的符号表示： $\left | A \right |,det(A)$

行列式的计算结果：一个数

计算模型1：二阶行列式

二阶行列式： $\begin{vmatrix} a &b\\ c & d \end{vmatrix}=ad-bc$

三阶行列式： $\begin{vmatrix} 3 & 0 & 4 \\ 2 & -1 & 7 \\-5 & 3 & 1\end{vmatrix}$

n阶行列式： $\begin{vmatrix}a_{11} & a_{12} & \ldots & a_{1n}\\ a_{21} & a_{22} & \ldots & a_{2n}\\ \vdots & \vdots & \ddots & \vdots\\ a_{n1} & a_{n2} & \ldots & a_{nn}\end{vmatrix}$

🍎计算行列式 $\begin{vmatrix} 1&-1\\ 4&2 \end{vmatrix}$

$\begin{vmatrix} 1&-1\\ 4&2 \end{vmatrix}=1\times 2-\left ( -1 \right )\times 4=6$

计算模型2：上三角形行列式

上三角形行列式特征：主对角线下皆为0。

上三角形行列式： $\begin{vmatrix} a_{11} & a_{12} & a_{13} \\ 0 & a_{22} & a_{23} \\ 0 & 0 & a_{33} \end{vmatrix}=a_{11}a_{22}a_{33}$

化上三角形通用方法：主对角线下，逐列变0。

2. 行列式的性质

性质1：倍加值不变

某行(列)加减另一行(列)的几倍，行列式的值不变。

行：row

列：column

🍎计算行列式 $\begin{vmatrix} 1 & -2 & 4 \\ 1 & 1 & 2 \\ 3 & 9 & 5 \end{vmatrix}.$

$\begin{vmatrix} 1 & -2 & 4 \\ 1 & 1 & 2 \\ 3 & 9 & 5 \end{vmatrix}\frac{r_2-1r_1}{r_3-3r_1} \begin{vmatrix} 1 & -2 & 4 \\ 0 & 3 & -2 \\ 0 & 15 & -7 \end{vmatrix}$

$\begin{vmatrix} 1 & -2 & 4 \\ 1 & 1 & 2 \\ 3 & 9 & 5 \end{vmatrix}= \begin{vmatrix} 1 & -2 & 4 \\ 0 & 3 & -2 \\ 0 & 15 & -7 \end{vmatrix}= \begin{vmatrix} 1 & -2 & 4 \\ 0 & 3 & -2 \\ 0 & 0 & 3 \end{vmatrix}=1\times3\times3=9$

🍎计算行列式 $\begin{vmatrix} 1 & 2 & 3 \\ -2 & 0 & -5 \\ 5 & 6 & 7 \end{vmatrix}.$

$\begin{vmatrix} 1 & 2 & 3 \\ -2 & 0 & -5 \\ 5 & 6 & 7 \end{vmatrix}= \begin{vmatrix} 1 & 2 & 3 \\ 0 & 4 & 1 \\ 0 & -4 & -8 \end{vmatrix}= \begin{vmatrix} 1 & 2 & 3 \\ 0 & 4 & 1 \\ 0 & 0 & -7 \end{vmatrix}=1\times4\times(-7)=-28$

性质2：互换要变号

互换行列式的某两行(列),行列式变号。

🍎计算行列式 $\begin{vmatrix} 2 & 3 & 5 \\ 0 & 0 & 1 \\ 0 & 4 & 7 \end{vmatrix}.$
$\begin{vmatrix} 2 & 3 & 5 \\ 0 & 0 & 1 \\ 0 & 4 & 7 \end{vmatrix}\quad\underline{r_2\leftrightarrow r_3}\quad-\quad \begin{vmatrix} 2 & 3 & 5 \\ 0 & 4 & 7 \\ 0 & 0 & 1 \end{vmatrix}\quad=-(2\times4\times1)=-8$