我们的PriorityQueue默认为最小堆，堆顶总是为最小 

215数组中的第K个最大元素

题目

思路解析

暴力解法（不符合时间复杂度）

题目要求我们找到「数组排序后的第 k 个最大的元素，而不是第 k 个不同的元素」。「数组排序后的第 k 个最大的元素」换句话说：从右边往左边数第 k 个元素（从 1 开始），那么从左向右数是第几个呢，我们列出几个找找规律就好了。

一共 6 个元素，找第 2 大，下标是 4；

一共 6 个元素，找第 4 大，下标是 2。

因此升序排序以后，目标元素的下标是 N−k，这里 N 是输入数组的长度

Arrays.sort(nums);
return nums[nums.length - k];

---

优先队列解法（堆）

我们维护一个数量为K的优先队列

我们的PriorityQueue默认为最小堆，堆顶总是为最小

所以我们一次遍历，每次数量大于K的时候踢出最小的

这样子我们遍历完后，我们就留下来了k个最大的值，第一个堆顶元素就是第K个最大的元素

---

最小堆的进一步优化

当我们的堆里元素为K个时，此时我们的要添加的num小于堆里面的最小值

我们可以不添加直接continue跳过

为什么一定要堆里面元素个数到k个的时候呢？

因为要是我们的数组元素总个数==K的时候

我们按那个跳过逻辑来弄，我们示例【2，1】，k=2

我们for循环会导致我们的元素【2】进去了堆，但是我们的元素【1】没进去堆，导致漏添加了元素

---

代码

暴力解法（不符合时间复杂度）

class Solution {
    public int findKthLargest(int[] nums, int k) {



       Arrays.sort(nums);
       return nums[nums.length - k];

       
    }

}

---

优先队列解法（堆）

class Solution {
    public int findKthLargest(int[] nums, int k) {

        PriorityQueue<Integer> heap=new PriorityQueue<>();
        for(int num:nums){
            heap.add(num);
            if(heap.size()>k){
                heap.poll();
            }   
        }

    return heap.peek();

       
    }

}

---

最小堆的进一步优化

class Solution {
    public int findKthLargest(int[] nums, int k) {

        PriorityQueue<Integer> heap=new PriorityQueue<>();
        for(int num:nums){

            if(heap.size()==k&&num<heap.peek())
            continue;

            heap.add(num);

            if(heap.size()>k){
                heap.poll();
            }   
        }

    return heap.peek();

       
    }

}

---

347前K个高频元素

题目

思路解析

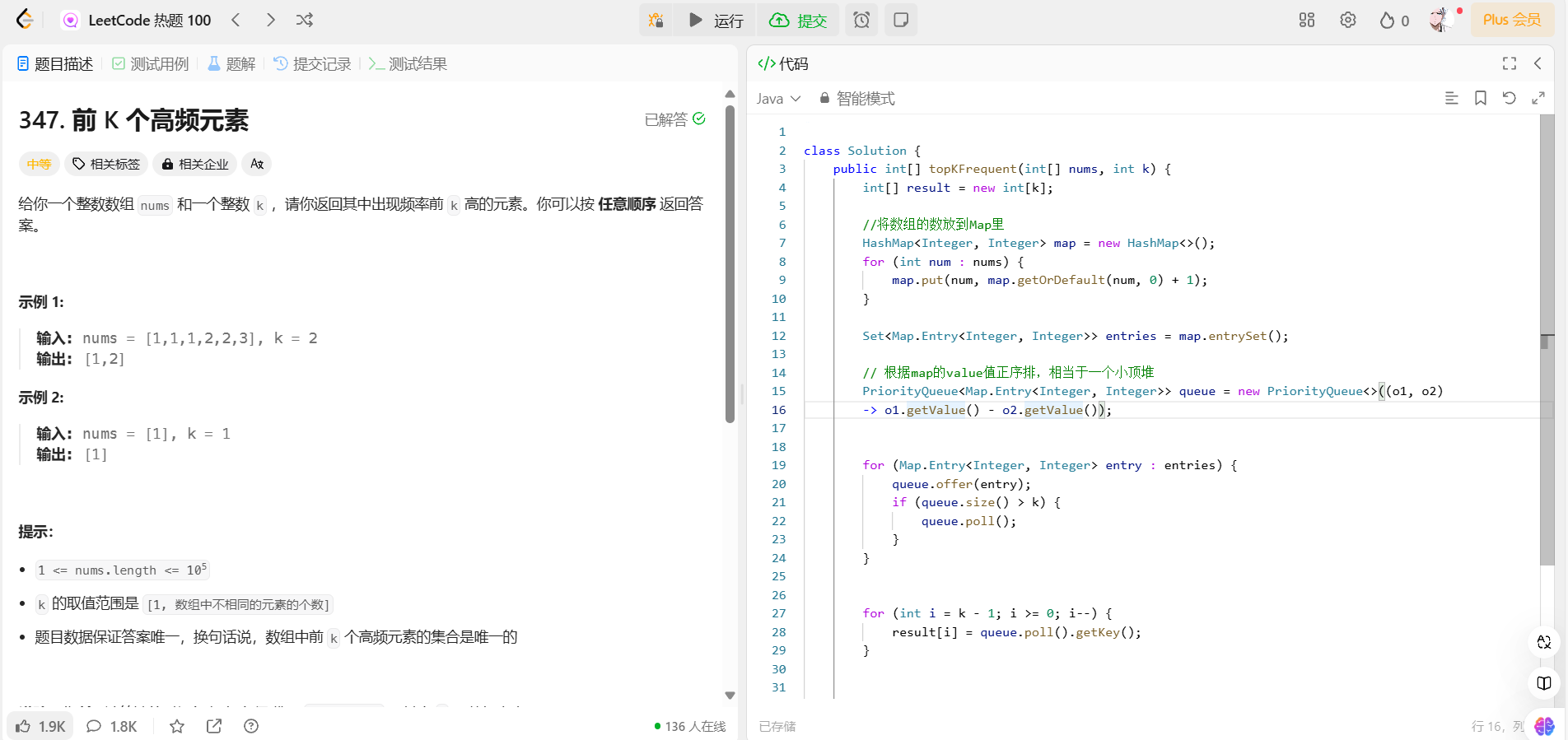
首先我们把所有的值到放到Map结构里面

然后我们把这个Map结构map.entrySet（）弄到Map结构里面

弄一个小顶堆，我们根据value来进行排序，正序，从小到大

Set<Map.Entry<Integer, Integer>> entries = map.entrySet();

// 根据map的value值正序排，相当于一个小顶堆
PriorityQueue<Map.Entry<Integer, Integer>> queue = new PriorityQueue<>((o1, o2) 
-> o1.getValue() - o2.getValue());

我们把EntrySet结构加入到优先队列，他会按照value大小，正序，从小到大排序

for (Map.Entry<Integer, Integer> entry : entries) {
            queue.offer(entry);
            if (queue.size() > k) {
                queue.poll();
            }
        }

遍历顺序

我们因为是小顶堆，但是我们最前面的一个是我们的频率最大的值

所以我们result【】数组要倒序加入我们的值

for (int i = k - 1; i >= 0; i--) {
            result[i] = queue.poll().getKey();
        }

代码

class Solution {
    public int[] topKFrequent(int[] nums, int k) {
        int[] result = new int[k];

        //将数组的数放到Map里
        HashMap<Integer, Integer> map = new HashMap<>();
        for (int num : nums) {
            map.put(num, map.getOrDefault(num, 0) + 1);
        }

        Set<Map.Entry<Integer, Integer>> entries = map.entrySet();

        // 根据map的value值正序排，相当于一个小顶堆
        PriorityQueue<Map.Entry<Integer, Integer>> queue = new PriorityQueue<>((o1, o2) 
        -> o1.getValue() - o2.getValue());

    
        for (Map.Entry<Integer, Integer> entry : entries) {
            queue.offer(entry);
            if (queue.size() > k) {
                queue.poll();
            }
        }


        for (int i = k - 1; i >= 0; i--) {
            result[i] = queue.poll().getKey();
        }

        
        return result;
    }
}

---

295数据流的中位数 

题目

思路解析

left最大堆和right最小堆的意义

中位数把这 6 个数均分成了左右两部分，一边是 left=[1,2,3]，另一边是 right=[4,5,6]。

我们要计算的中位数，就来自 left 中的最大值，以及 right 中的最小值

随着 addNum 不断地添加数字，我们需要：

1.保证 left 的大小和 right 的大小尽量相等。规定：在有奇数个数时，left 比 right 多 1 个数。

2.保证 left 的所有元素都小于等于 right 的所有元素。

只要时时刻刻满足以上两个要求（满足中位数的定义），我们就可以用 left 中的最大值以及 right 中的最小值计算中位数

分类讨论

如果当前 left 的大小和 right 的大小相等(并下一步往right添加元素)

如果添加的数字 num 比较大，比如添加 7，那么把 7 加到 right 中。

现在 left 比 right 少 1 个数，不符合前文的规定，所以必须把 right 的最小值从 right 中去掉，添加到 left 中。如此操作后，可以保证 left 的所有元素都小于等于 right 的所有元素。

如果添加的数字 num 比较小，比如添加 0，那么把 0 加到 left 中。

这两种情况可以合并：无论 num 是大是小，都可以先把 num 加到 right 中，然后把 right 的最小值从 right 中去掉，并添加到 left 中。

如果当前 left 比 right 多 1 个数（并下一步往left添加元素）

如果添加的数字 num 比较大，比如添加 7，那么把 7 加到 right 中。

如果添加的数字 num 比较小，比如添加 0，那么把 0 加到 left 中。现在 left 比 right 多 2 个数，不符合前文的规定，所以必须把 left 的最大值从 left 中去掉，添加到 right 中。如此操作后，可以保证 left 的所有元素都小于等于 right 的所有元素。

这两种情况可以合并：无论 num 是大是小，都可以先把 num 加到 left 中，然后把 left 的最大值从 left 中去掉，并添加到 right 中

总结

我们left是最大堆

我们right是最小堆

left.size（）==right.size（）的情况

然后我们往right添加元素,然后right是最小堆，我们让right中元素的最小值移动到left，变成left.size（）>right.size（）的情况

此时就是left.size（）>right.size（）的情况

我们往left添加元素，然后left是最大堆，我们让left中元素的最大值移动到right,这样子又变成了元素个数相等的情况

如果我们的left.size（）>right.size（），因为我们的逻辑让left中的元素只能比right中最多多一个

所以此时left的最大值就是中位数

如果我们的left.size（）==right.size（），我们的中位数是【（left的最大值）+（right的最小值）】/2.0

代码

class MedianFinder {
    //最大堆
    private final PriorityQueue<Integer> left=new PriorityQueue<>((a,b)->b-a);
    //最小堆
    private final PriorityQueue<Integer> right=new PriorityQueue<>();

    public MedianFinder() {

    }
    
    public void addNum(int num) {
        if(left.size()==right.size()){//两个堆内元素个数相等的情况,我们往right添加元素
        //然后弹出right的最小值加入到left里面
            right.offer(num);
            left.offer(right.poll());
        }else{//当left的元素>right的元素,我们往left添加元素
        //然后弹出left的最大值加入到right里面
            left.offer(num);
            right.offer(left.poll());
        }        
    }
    
    public double findMedian() {
        if(left.size()>right.size()){
            return left.peek();
        }

        return(left.peek()+right.peek())/2.0;

    }
}

/**
 * Your MedianFinder object will be instantiated and called as such:
 * MedianFinder obj = new MedianFinder();
 * obj.addNum(num);
 * double param_2 = obj.findMedian();
 */