刷题总结回溯算法

为了方便复习并且在把算法忘掉的时候能尽量快速的捡起来

刷完回溯算法这里需要做个总结

回溯算法的适用范围

回溯算法是深度优先搜索（DFS）的一种特定应用，在DFS的基础上引入了约束检查和回退机制。

相比于普通的DFS，回溯法的优势主要体现在解决需要约束条件判断、剪枝和回退的复杂问题上。

实际应用时有易于识别的题目类型特征：组合、分割、子集、排列、棋盘等

这些问题的共同点是解空间均为层次结构，因此回溯算法就是对回溯树进行DFS

模式识别

根据自己刷题的感受，并统计做题过程中思路上遇到过的槛，

归纳后可以得到以下模式识别树，

专门用于看到题目后进行模式识别，

快速找到解题方法：

该模式识别树综合搜索集类型、搜索规则和结果收集条件等因素

接下来对当前的模式识别树进行简单解释：

回溯算法总模板：

def backtracking(self, 参数):
    if 终止条件
        存放结果
        return

    for 选择：本层集合中元素（树中节点孩子的数量就是集合的大小）:
        处理节点
        self.backtracking(路径，选择列表) // 递归
        回溯，撤销处理结果

步骤：1.函数（无返回值，参数多） + 2.if（终止）{收集+return} + 3.for（搜索集）{处理；递归；回溯}

回溯树：

一、题目类型

回溯算法常用于解决问题：组合、分割、子集、排列、棋盘等

在我眼里以上题目类型可以总结为三个大类：组合类问题、排列类问题和约束满足类问题，

因此，这几个大类是根据解空间（回溯树）的层次结构进行划分的，

而且对模板的应用有较大的影响

1.组合类问题：层内层间顺序访问

包含类型：组合、分割、子集

模板变体：

def backtracking(self, 输入参数, start_idx, path, ans):
    if 终止条件
        存放结果
        return

    for i in range(start_idx, len(总搜索集)):
        if 约束条件：
            continue # 有时需要break
        处理节点
        self.backtracking(输入参数, start_idx + 1, path, ans) // 递归
        回溯，撤销处理结果

或

def backtracking(self, 输入参数, start_idx, path, ans):
    if 终止条件
        存放结果
        return

    for i in range(start_idx, len(总搜索集)):
        if 约束条件：
            处理节点
            self.backtracking(输入参数, start_idx + 1, path, ans) // 递归
            回溯，撤销处理结果

模式识别特征：

不考虑顺序
一般搜索集长度大于结果长度
回溯树层内层间顺序访问

题目列表：

组合

77. 组合

216. 组合总和 III

39. 组合总和

40. 组合总和 II

分割

131. 分割回文串

93. 复原 IP 地址

子集

78. 子集

90. 子集 II

491. 非递减子序列

这其中有一个特例就是重复选取题：39. 组合总和

递归命令需要改为：

# self.backtracking(输入参数, start_idx + 1, path, ans) // 递归
self.backtracking(输入参数, start_idx, path, ans) // 递归

2.排列类问题：层内遍历访问层间顺序访问

包含类型：排列

模板变体：

该类型题目有visited数组写法、集合写法和交换元素三种写法，

visited数组普适性较强，以visited数组写法为例：

def backtracking(self, 输入参数, visited, path, ans):
    if 终止条件
        存放结果
        return

    for i in range(len(总搜索集)):
        if visited[i] or 其他约束条件：
            continue
        处理节点
        visited[i] = True
        self.backtracking(输入参数, visited, path, ans) // 递归
        visited[i] = False
        其他回溯，撤销处理结果

模式识别特征：

考虑顺序
搜索集长度等于结果长度
回溯树层内遍历，层间顺序访问

题目列表：

46. 全排列

47. 全排列 II

3.约束满足问题：约束条件较强，无特定访问顺序

包含类型：安排行程、棋盘

相比于总模板无特定要求，但常需要主函数预处理搜索集以剪枝回溯树，实现高效搜索

模式识别特征：

一般类似于排列问题
有较强的约束条件
一般需要对搜索集预处理，否则会超时或代码过于复杂

题目列表：

332. 重新安排行程

棋盘

51. N 皇后

37. 解数独

二、几个需要注意的题目类型的约束条件

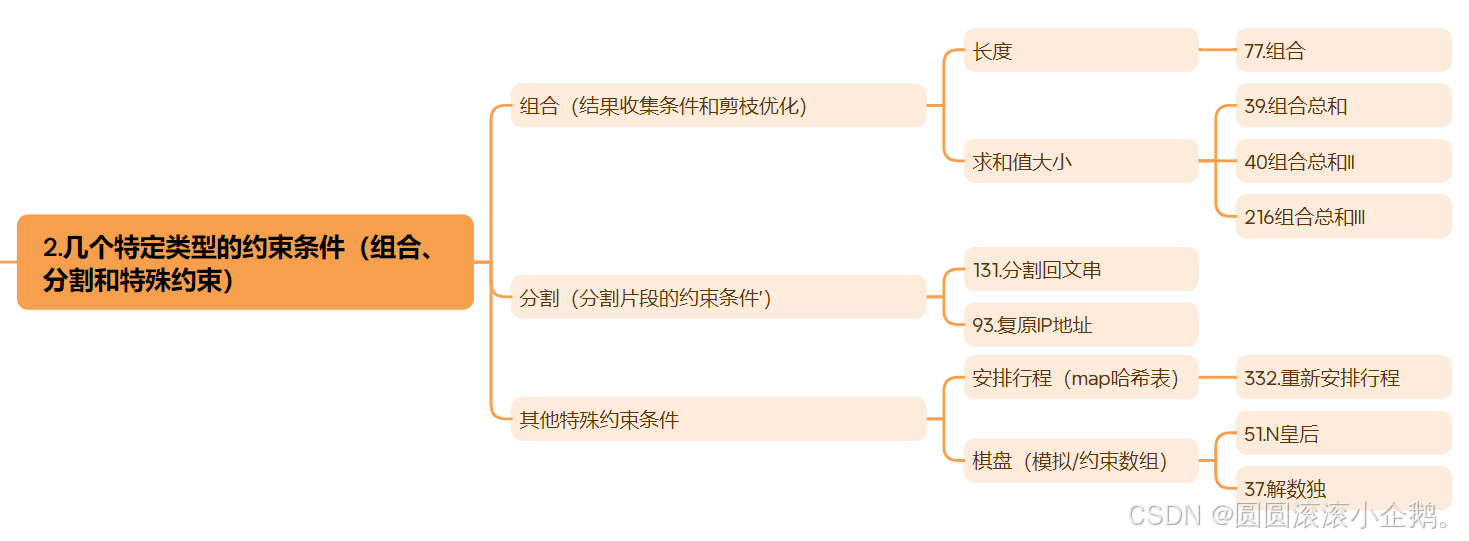
这个只有一个维度，目前共遇到三个种类：

1.组合：结果收集条件和剪枝优化

1.1 长度

用长度作为结果收集条件会产生两个结果：

（1）路径长度符合条件时收集结果并返回

（2）剪枝优化：搜索集末尾剪枝

可以通过控制单个节点内下一步访问的搜索集的末尾位置

实现方式未

把回溯树的末端指针从n调整到n - (k - len(path)) + 1

题目：

77. 组合

理解起来就是把末尾的(k - len(path))个路径去掉，

以长度作为结果收集条件的题目总搜索集长度 > 路径长度 + 节点内搜索集宽度

节点内搜索集宽度太大了，路径长度就达不到要求，

所以需要把回溯树的宽度从n调整到n - (k - len(path)) + 1，

末尾的+1是本轮访问的节点

1.2 求和值大小

类似于长度，也是有两个影响：

（1）路径求和等于目标数时收集结果并返回，大于目标数直接返回

（2）剪枝优化：排序break剪枝，

将搜索集排序，求和大于目标数舍弃节点所有后续路径

题目：

216. 组合总和 III

39. 组合总和

40. 组合总和 II

实现方式为：

如果下一层的sum（就是本层的 sum + candidates[i]）已经大于target，就可以结束本轮for循环的遍历

注意主函数种要对总搜索集排序

2.分割：分割片段的约束条件

分割类题目对分割片段有特殊的要求，因此常采用以下模板范式：

def is_valid(self, 参数):
    判断条件

def backtracking(self, 输入参数, start_idx, path, ans):
    if 终止条件
        存放结果
        return

    for i in range(start_idx, len(总搜索集)):
        if self.is_valid(参数)：
            处理节点
            self.backtracking(输入参数, start_idx + 1, path, ans) // 递归
            回溯，撤销处理结果

题目：

131. 分割回文串

93. 复原 IP 地址

3.其他特殊约束条件：棋盘、安排行程等

该类题，常常需要复杂的判断条件或在主函数中对搜索集预处理（常用哈希表）来辅助判断约束条件

其中复杂的判断条件可能导致超时，

在主函数中对搜索集预处理（常用哈希表）来辅助判断比较常用

题目：（预处理方式）

安排行程：map哈希表：

332. 重新安排行程

棋盘：数组哈希表：

51. N 皇后

37. 解数独

三、去重

1.组合问题中的去重

如果搜索集存在重复元素，则需要进行同层重复剪枝操作来去重，

否则由于回溯树中同一层存在重复元素，使得多条路径通向同一个结果

导致重复的组合结果，

去重方法可以分为索引去重和数值去重，但都需要排序，

其中排序有两个作用：使相同数字紧贴和防止异层重复访问

防止异层重复访问是去重能够在层内进行的前提，

索引去重便是利用相同数字紧贴的特性去重，有简单写法和数组写法两种写法

数值去重则是在层内统计同一个数值的使用情况来去重，不需要排序的第一个功能，

更详细介绍在刷题记录回溯算法-13：90. 子集 II-CSDN博客

题目：

40. 组合总和 II

90. 子集 II

491. 非递减子序列

其中491. 非递减子序列情况特殊，只能用数值去重，详见刷题记录回溯算法-14：491. 非递减子序列-CSDN博客

2.排列问题中的去重

和组合问题略有不同，排列问题除了层内去重还可以倒序去重，

层内去重逻辑和组合去重类似，索引去重和数值去重都可以用，同样需要排序，

但索引去重的简单写法无法使用，只能用数组写法

倒序去重很少用，以上详见：

刷题记录回溯算法-16：47. 全排列 II-CSDN博客

题目：47. 全排列 II

四、遍历与搜索（递归函数返回）

大部分题目需要找到所有结果，但有些题目找到一个结果即可返回，其代码结构会出现一些变化

1.收集所有结果

大部分题目都需要用一个数组收集所有符合条件的结果，

这也是总模板适配的情况

def backtracking(self, 参数):
    if 终止条件
        存放结果
        return

    for 选择：本层集合中元素（树中节点孩子的数量就是集合的大小）:
        处理节点
        self.backtracking(路径，选择列表) // 递归
        回溯，撤销处理结果

2.找到一个结果

有些题目只需要找到一个结果即可，且往往尝试找到所有结果会导致超时，

这种情况需要用返回值在找到结果后快速返回主函数：

def backtracking(self, 参数):
    if 终止条件
        存放结果
        return True

    for 选择：本层集合中元素（树中节点孩子的数量就是集合的大小）:
        处理节点
        if self.backtracking(路径，选择列表):  # 递归
            return True
        回溯，撤销处理结果
    return False

修改分为三处：

1.终止条件返回True

2.递归调用返回True

3.函数末尾返回False

题目：

332. 重新安排行程

37. 解数独