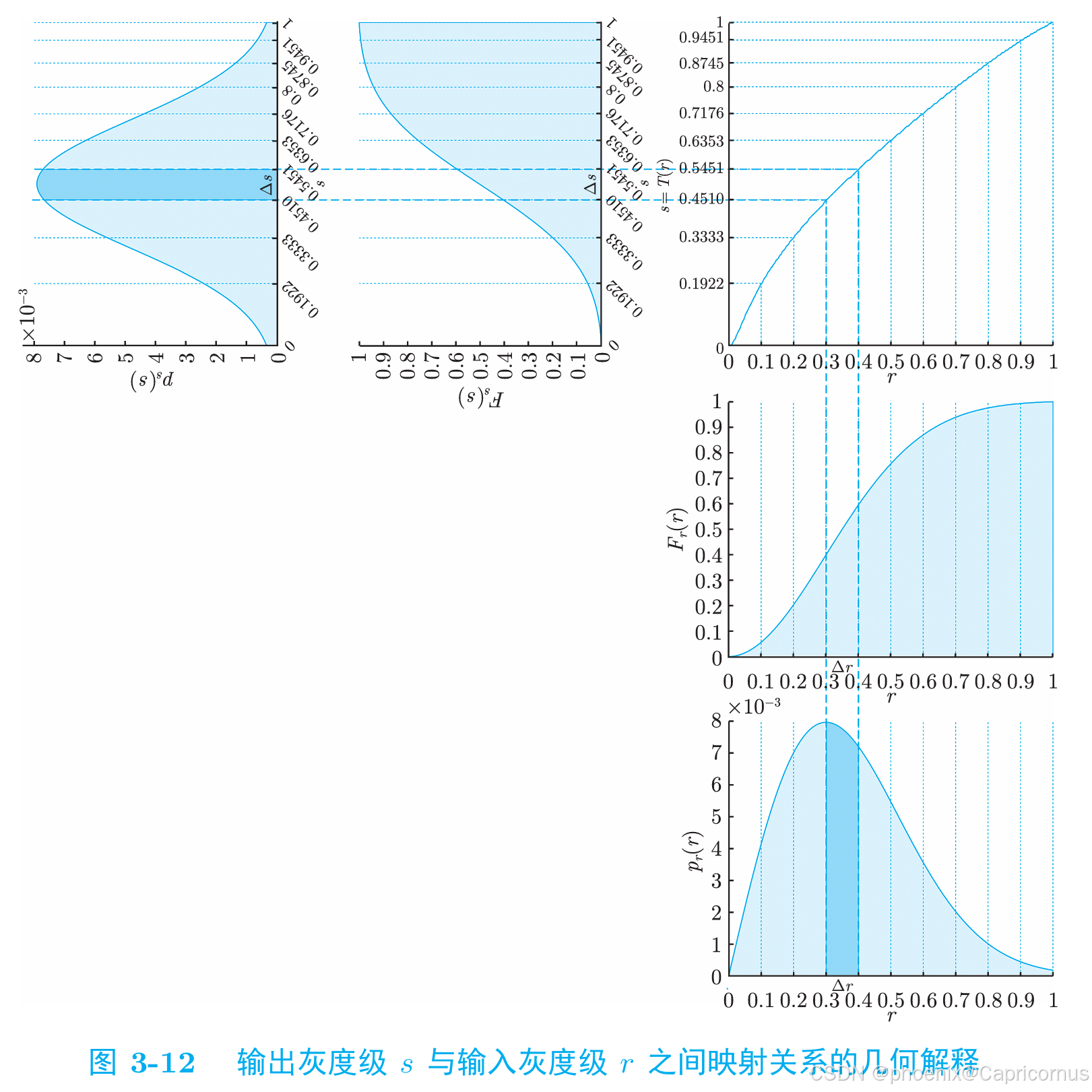
对于连续型随机变量,分布函数(Cumulative Distribution Function, CDF)是概率密度函数(Probability Density Function, PDF)的变上限积分,概率密度函数是分布函数的导函数。
如果我们有一个连续型随机变量 X X X,其分布函数记为 F ( x ) F(x) F(x),而其概率密度函数记为 f ( x ) f(x) f(x),那么两者之间的关系可以通过微积分来描述:
F ( x ) = ∫ − ∞ x f ( t ) d t F(x) = \int_{-\infty}^{x} f(t) \, dt F(x)=∫−∞xf(t)dt
根据微积分的基本定理,如果 f ( x ) f(x) f(x)是连续的,则有:
f ( x ) = d d x F ( x ) f(x) = \frac{d}{dx} F(x) f(x)=dxdF(x)
这表明在任意点
x
x
x,概率密度函数
f
(
x
)
f(x)
f(x)给出了分布函数
F
(
x
)
F(x)
F(x)在该点的变化率,即斜率。换句话说,概率密度函数表示了分布函数在每一点上的瞬时变化速度。

需要注意的是,这个关系只对连续型随机变量成立。对于离散型随机变量,我们没有概率密度函数的概念,因为离散型随机变量的概率分布在离散的点上具有非零值,而在这些点之外的概率为零。
对于离散型随机变量,我们通常讨论的是分布列(Probability Mass Function, PMF),它给出了随机变量取特定离散值的概率。
在图像处理中,直方图本质上就是概率密度函数(PDF),累积直方图本质上就是分布函数(CDF)。离散与连续之分。