1.圆排列
问题描述
GXUOJ | 圆排列

代码解答
#include<bits/stdc++.h>
using namespace std;
int n;
int r[1000];
double x[1000];
double ans = 0x3f3f3f3f;
double calculate(){
memset(x, 0, sizeof x);
for(int i = 0; i < n; i++){
for(int j = 0; j < i; j++)
x[i] = max(x[i], x[j] + sqrt(4*r[i]*r[j]));
}
double low = 0x3f3f3f3f, high = - 0x3f3f3f3f;
for(int i = 0; i < n; i++){
low = min(low, x[i] - r[i]);
high = max(high, x[i] + r[i]);
}
return high - low;
}
int main(){
cin >> n;
for(int i = 0; i < n; i++)
cin >> r[i];
do{
ans = min(ans, calculate());
}while(next_permutation(r, r + n));
printf("%.2lf", floor(ans * 100)/100);
}但是这个算法考虑的全是圆相切的情况,并没有考虑如下的情况
圆排列问题详解(原理+代码)_对n个圆的最优排列问题,深度优先遍历其排列树所需要的辅助空间-CSDN博客
代码更改
#include<bits/stdc++.h>
using namespace std;
const int MAXLEN =1000;
double r[MAXLEN];//存放圆排列的半径
double x[MAXLEN];//存放圆排列的圆心横坐标
double best_r[MAXLEN];//用来记录结果
int N;//输入圆的个数
double minlen=1000;
void compute(){
//找到了一个排列 且此半径排列存放在数组r中
double low=0,high=0;
for(int i=1;i<=N;i++){//算出每一个圆的左边界和右边界
if(x[i]-r[i] < low) low = x[i]-r[i];
if(x[i]+r[i] > high) high = x[i]+r[i];
}
if(high-low<minlen){
minlen=high-low;//更新最小长度
for(int i=1;i<=N;i++) best_r[i]=r[i];//记录最小排列
}
}
double center(int t){//计算圆心坐标
double x_max=0;
for(int j=1;j<t;j++){//t=1的时候 第一个圆不计算 横坐标记为0
double x_value=x[j]+2.0*sqrt(r[t]*r[j]);
if(x_value>x_max) x_max=x_value;//取最大的那个计算值
}
return x_max;
}
void backtrack(int index){
if(index==N+1){//已经找到了一个排列
compute();
}
else{
for(int j=index;j<=N;j++){//index之前的已经排列好 index位置依次与后面的交换
swap(r[index],r[j]);
double center_x=center(index);//计算当前第t个位置的横坐标
if(center_x+r[index]+r[1]<minlen){//如果已经大于维护的最小值 则不必搜索
x[index]=center_x;//存入表示坐标的数组x中
backtrack(index+1);//递归选择index+1位置
}
swap(r[index],r[j]);//index选择j的情况已经结束 把他换回去 进行下一个交换
}
}
}
int main(){
cin>>N;//一共N个圆
for(int i=1;i<=N;i++){
cin>>r[i];//输入所有圆的半径
}
backtrack(1);
//输出结果
printf("%.2f",minlen-0.005);
return 0;
}
2.连续邮资
问题描述
GXUOJ | 连续邮资

代码解答
#include<bits/stdc++.h>
using namespace std;
int n, m;//n为邮票种类,m为一封信上最多贴的邮票个数
int Max;
int ans[10000];//最终答案数组
//能否用n种邮票,面值在x数组中,最多贴m张,表示出sum(是个动态规划问题,
//方法是求出dp[n][sum]看它是否小于sum,状态转移方程
//dp[i][j]=min(dp[i-1][j-k*x[i]]+k)(其中dp[i][j]表示用到第i种邮票,
//表示邮资为j的最少邮票
bool panduan(int x[], int n, int sum){
//dp[i][j]来表示使用前i种邮票凑出邮资j所需的最少邮票数
int dp[15][1005]={0};
for (int i = 1; i <= sum; i++)
dp[1][i] = i;
for (int i = 2; i <= n; i++){
for (int j = 1; j <= sum; j++){
dp[i][j] = 9999;
for (int k = 0; k <= j / x[i]; k++)
dp[i][j] = min(dp[i][j], dp[i - 1][j - x[i] * k] + k);
}
}
if (dp[n][sum] > m)
return false;
return true;
}
void DFS(int x[], int cur, int max){
if (cur == n){//如果已经得出了n种邮票
if (max > Max){//并且它的最大值已经大于当前最大邮资数
Max = max;
for (int i = 1; i <= cur; i++)
ans[i] = x[i];//更新答案数组
}
return;
}
for (int next = x[cur] + 1; next <= max + 1; next++)//如果还没得到n中邮票,那么从x[cur]+1~max+1选一个作为下一个邮资,因为max+1没法表示,所以必定到max+1为止
{
x[cur + 1] = next;
//接下来是重点,用种类为cur+1,数目分别为x[1..cur+1]的邮票,最多使用m张,
//能否表示出大于max的某个数
int newMax=max;
for (int i = max + 1; i <= m * x[cur + 1]; i++){
//这个数最少要为max+1(不然没有意义了),最多是x[cur+1]*m
if (panduan(x, cur + 1, i) == 0)//如果成立
break;
newMax=i;
}
if (newMax> max)//如果至少让最大值更新了一次
DFS(x, cur + 1, newMax);
}
}
int main()
{
cin >> n >> m;
Max = 0;
int x[1000]={0};//中间传递的数组,存储当前的邮票值的解
x[1] = 1;
DFS(x, 1, m);//x存储当前的解,cur表示当前传递到第几种邮票,max表示目前能表示到的最大值
for (int i = 1; i <= n; i++)
cout<<ans[i] <<" ";
cout << endl;
cout << Max;
return 0;
}3.n皇后问题
问题描述
GXUOJ | n皇后问题

代码解答
#include <bits/stdc++.h>
using namespace std;
const int N = 20;
// bool数组用来判断搜索的下一个位置是否可行
// col列,dg对角线,udg反对角线
// g[N][N]用来存路径
int n;
char g[N][N];
bool col[N], dg[N], udg[N];
int result = 0;
void dfs(int u) {
// u == n 表示已经搜了n行,故输出这条路径
if (u == n) {
result++;
return;
}
// 枚举u这一行,搜索合法的列
int x = u;
for (int y = 0; y < n; y++)
// 剪枝(对于不满足要求的点,不再继续往下搜索)
if (col[y] == false && dg[y - x + n] == false && udg[y + x] == false) {
col[y] = dg[y - x + n] = udg[y + x] = true;
dfs(x + 1);
col[y] = dg[y - x + n] = udg[y + x] = false;
}
}
int main() {
cin >> n;
dfs(0);
cout << result;
return 0;
}4.符号三角形
问题描述
GXUOJ | 符号三角形

代码解答
#include <bits/stdc++.h>
using namespace std;
// n 表示符号三角形第一行的元素个数
// cnt 用于积累符号三角形中1的元素个数
int n, cnt = 0;
// sum 用于统计满足条件的符号三角形的数量
int sum = 0;
// p 数组用于存储符号三角形,p[i][j] 表示第 i 行第 j 列的元素
int p[25][25];
// 回溯函数,t 表示当前处理到符号三角形第一行的第 t 个位置
void back(int t) {
// 剪枝条件:如果当前已经确定的 1 的数量超过了总数的二分之一,或者剩余位置全为 1 时 1 的数量仍超过总数的二分之一,就返回
// n*(n + 1)/4 是因为整个符号三角形元素总数为 n*(n + 1)/2 ,1 的数量如果超过一半,就不可能满足 0 和 1 数量相等
// t*(t - 1)/2 - cnt 表示假设剩余位置全为 1 时 1 的数量
//前t行总元素为 t*(t+1)/2 ,减去 t和 cnt 假设剩余位置全为 1 时 1 的数量
if (cnt > n * (n + 1) / 4 || t * (t - 1) / 2 - cnt > n * (n + 1) / 4) return;
// 如果已经处理完符号三角形第一行的所有元素,说明成功构建了一个符号三角形
if (t > n) sum++;
else
// 尝试在当前位置放置 0 或 1
for (int i = 0; i < 2; i++) {
// 在符号三角形第一行的第 t 个位置放置 i
p[1][t] = i;
// 更新当前已确定的 1 的数量
cnt += i;
// 根据上一行的元素确定当前行的元素
for (int j = 2; j <= t; j++) {
// 通过异或运算确定当前位置的元素,这里用异或模拟符号三角形的生成规则
p[j][t - j + 1] = p[j - 1][t - j + 1] ^ p[j - 1][t - j + 2];
// 更新当前已确定的 1 的数量
cnt += p[j][t - j + 1];
}
// 递归处理下一个位置
back(t + 1);
// 回溯,恢复之前的状态,减去当前行已确定的 1 的数量
for (int j = 2; j <= t; j++) {
cnt -= p[j][t - j + 1];
}
// 回溯,恢复之前的状态,减去当前位置放置的 1 的数量
cnt -= i;
}
}
int main() {
cin >> n;
// 从符号三角形第一行的第一个位置开始回溯
back(1);
cout << sum;
return 0;
}
没有注释版本
#include<bits/stdc++.h>
using namespace std;
int n,sum,cnt;
int p[25][25];
void back(int t){
if(cnt>(n+1)*n/4|| t*(t-1)/2-cnt>(n+1)*n/4) return;
if(t>n) sum++;
else{
for(int i=0;i<2;i++){
p[1][t]=i;
cnt+=i;
for(int j=2;j<=t;j++){
p[j][t-j+1]=p[j-1][t-j+1]^p[j-1][t-j+2];
cnt+=p[j][t-j+1];
}
back(t+1);
for(int j=2;j<=t;j++)
cnt-=p[j][t-j+1];
cnt-=i;
}
}
}
int main(){
cin>>n;
back(1);
cout<<sum;
return 0;
}![[创业之路-225]:《华为闭环战略管理》-4-华为的商业智慧:在价值链中探索取舍之道与企业边界](https://i-blog.csdnimg.cn/direct/7ac721d38ade407b961e933085d81474.png)





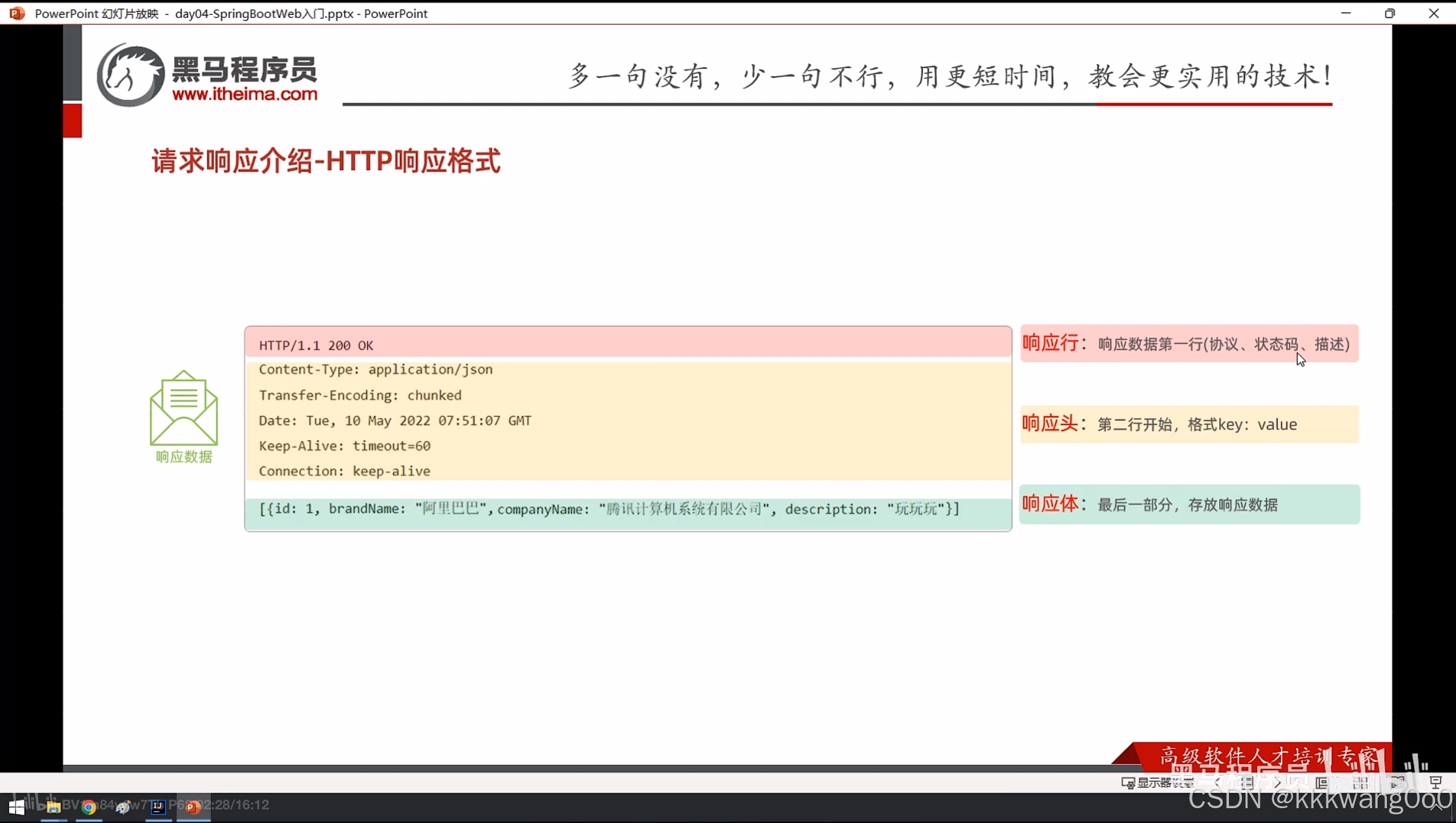




![Java [后端] 开发日常记录(1)](https://i-blog.csdnimg.cn/blog_migrate/b8c6a793712d05bde2bd3e323b0a4be0.png)







